Estimating Exoplanet Mass using Machine Learning on Incomplete Datasets

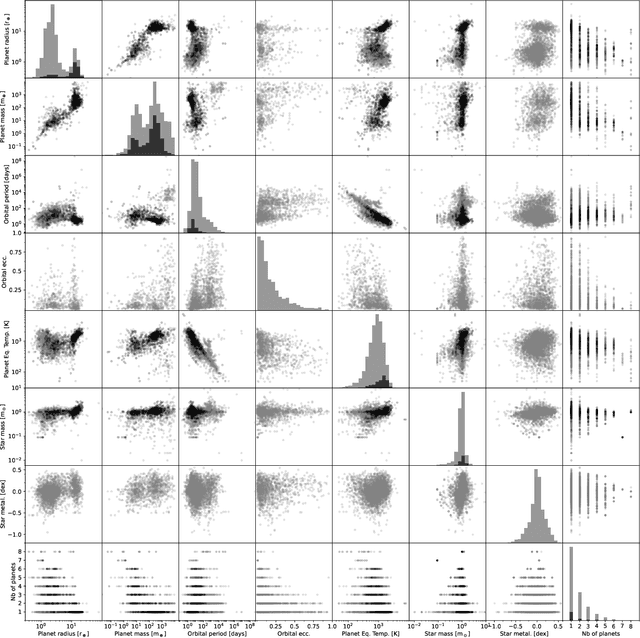
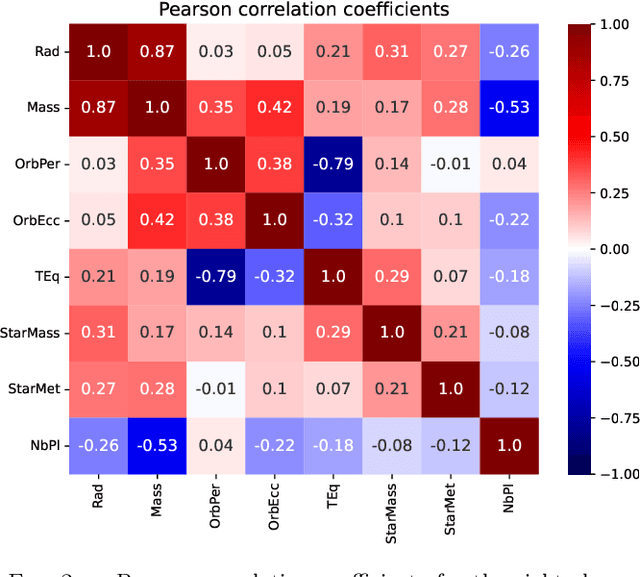
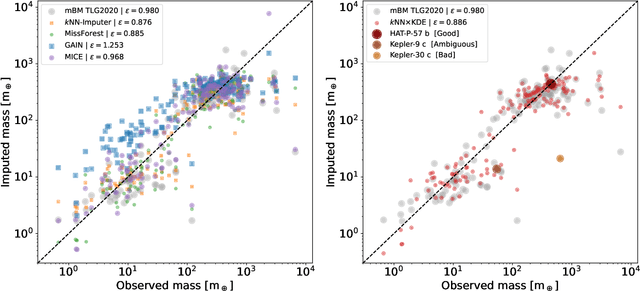
The exoplanet archive is an incredible resource of information on the properties of discovered extrasolar planets, but statistical analysis has been limited by the number of missing values. One of the most informative bulk properties is planet mass, which is particularly challenging to measure with more than 70\% of discovered planets with no measured value. We compare the capabilities of five different machine learning algorithms that can utilize multidimensional incomplete datasets to estimate missing properties for imputing planet mass. The results are compared when using a partial subset of the archive with a complete set of six planet properties, and where all planet discoveries are leveraged in an incomplete set of six and eight planet properties. We find that imputation results improve with more data even when the additional data is incomplete, and allows a mass prediction for any planet regardless of which properties are known. Our favored algorithm is the newly developed $k$NN$\times$KDE, which can return a probability distribution for the imputed properties. The shape of this distribution can indicate the algorithm's level of confidence, and also inform on the underlying demographics of the exoplanet population. We demonstrate how the distributions can be interpreted with a series of examples for planets where the discovery was made with either the transit method, or radial velocity method. Finally, we test the generative capability of the $k$NN$\times$KDE to create a large synthetic population of planets based on the archive, and identify potential categories of planets from groups of properties in the multidimensional space. All codes are Open Source.

A Transformer Model for Symbolic Regression towards Scientific Discovery

Symbolic Regression (SR) searches for mathematical expressions which best describe numerical datasets. This allows to circumvent interpretation issues inherent to artificial neural networks, but SR algorithms are often computationally expensive. This work proposes a new Transformer model aiming at Symbolic Regression particularly focused on its application for Scientific Discovery. We propose three encoder architectures with increasing flexibility but at the cost of column-permutation equivariance violation. Training results indicate that the most flexible architecture is required to prevent from overfitting. Once trained, we apply our best model to the SRSD datasets (Symbolic Regression for Scientific Discovery datasets) which yields state-of-the-art results using the normalized tree-based edit distance, at no extra computational cost.

Numerical Data Imputation for Multimodal Data Sets: A Probabilistic Nearest-Neighbor Kernel Density Approach

Numerical data imputation algorithms replace missing values by estimates to leverage incomplete data sets. Current imputation methods seek to minimize the error between the unobserved ground truth and the imputed values. But this strategy can create artifacts leading to poor imputation in the presence of multimodal or complex distributions. To tackle this problem, we introduce the $k$NN$\times$KDE algorithm: a data imputation method combining nearest neighbor estimation ($k$NN) and density estimation with Gaussian kernels (KDE). We compare our method with previous data imputation methods using artificial and real-world data with different data missing scenarios and various data missing rates, and show that our method can cope with complex original data structure, yields lower data imputation errors, and provides probabilistic estimates with higher likelihood than current methods. We release the code in open-source for the community: https://github.com/DeltaFloflo/knnxkde

Predicting the Stability of Hierarchical Triple Systems with Convolutional Neural Networks

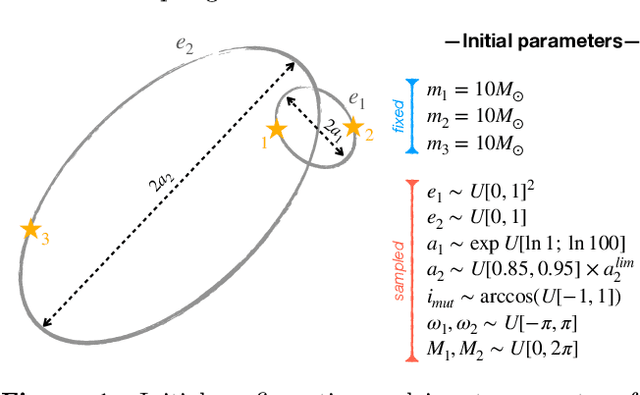
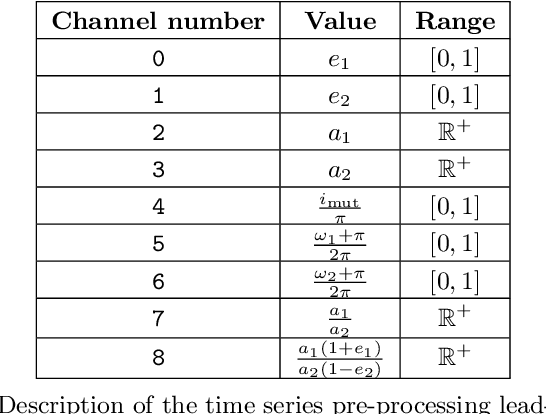
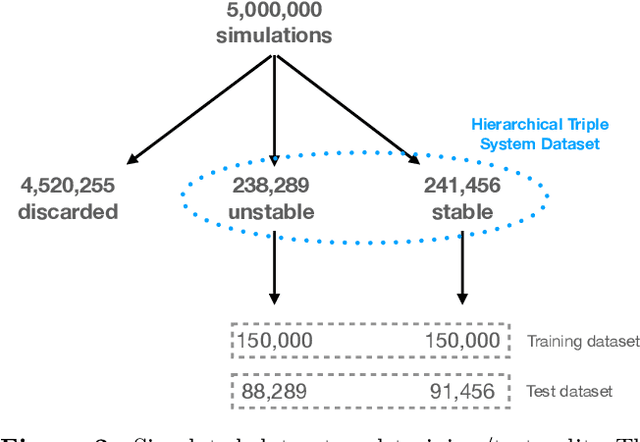
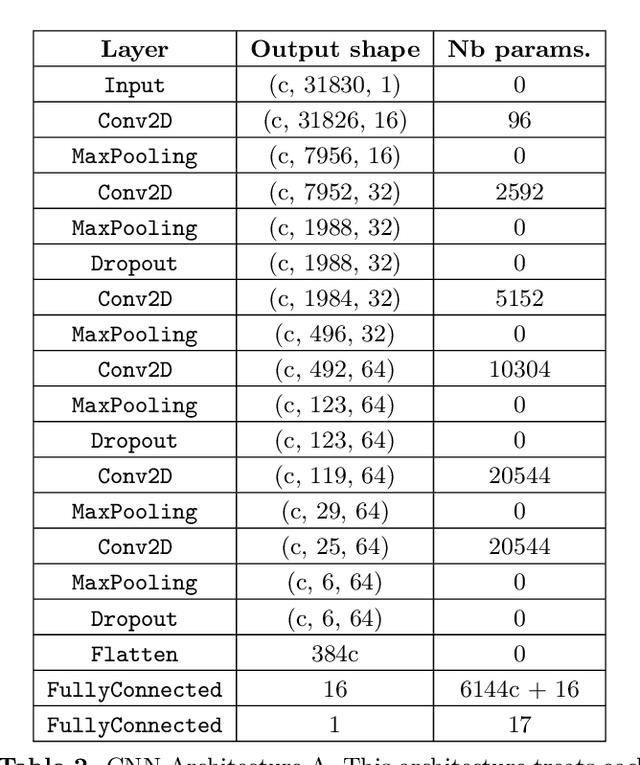
Understanding the long-term evolution of hierarchical triple systems is challenging due to its inherent chaotic nature, and it requires computationally expensive simulations. Here we propose a convolutional neural network model to predict the stability of hierarchical triples by looking at their evolution during the first $5 \times 10^5$ inner binary orbits. We employ the regularized few-body code \textsc{tsunami} to simulate $5\times 10^6$ hierarchical triples, from which we generate a large training and test dataset. We develop twelve different network configurations that use different combinations of the triples' orbital elements and compare their performances. Our best model uses 6 time-series, namely, the semimajor axes ratio, the inner and outer eccentricities, the mutual inclination and the arguments of pericenter. This model achieves an area under the curve of over $95\%$ and informs of the relevant parameters to study triple systems stability. All trained models are made publicly available, allowing to predict the stability of hierarchical triple systems $200$ times faster than pure $N$-body methods.

On the dissection of degenerate cosmologies with machine learning

Based on the DUSTGRAIN-pathfinder suite of simulations, we investigate observational degeneracies between nine models of modified gravity and massive neutrinos. Three types of machine learning techniques are tested for their ability to discriminate lensing convergence maps by extracting dimensional reduced representations of the data. Classical map descriptors such as the power spectrum, peak counts and Minkowski functionals are combined into a joint feature vector and compared to the descriptors and statistics that are common to the field of digital image processing. To learn new features directly from the data we use a Convolutional Neural Network (CNN). For the mapping between feature vectors and the predictions of their underlying model, we implement two different classifiers; one based on a nearest-neighbour search and one that is based on a fully connected neural network. We find that the neural network provides a much more robust classification than the nearest-neighbour approach and that the CNN provides the most discriminating representation of the data. It achieves the cleanest separation between the different models and the highest classification success rate of 59% for a single source redshift. Once we perform a tomographic CNN analysis, the total classification accuracy increases significantly to 76% with no observational degeneracies remaining. Visualising the filter responses of the CNN at different network depths provides us with the unique opportunity to learn from very complex models and to understand better why they perform so well.