Predicting the Stability of Hierarchical Triple Systems with Convolutional Neural Networks

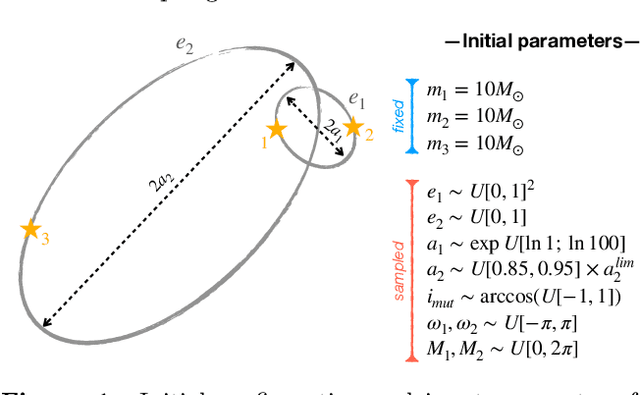
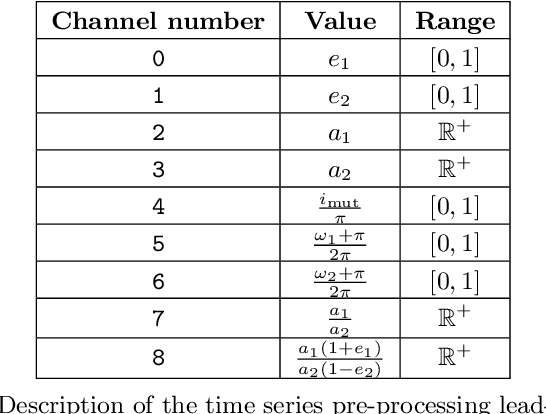
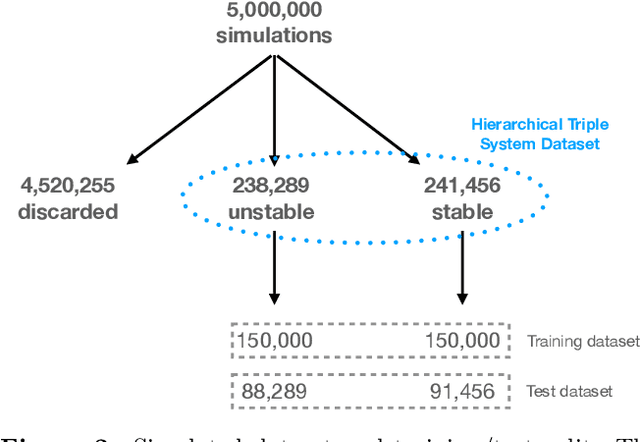
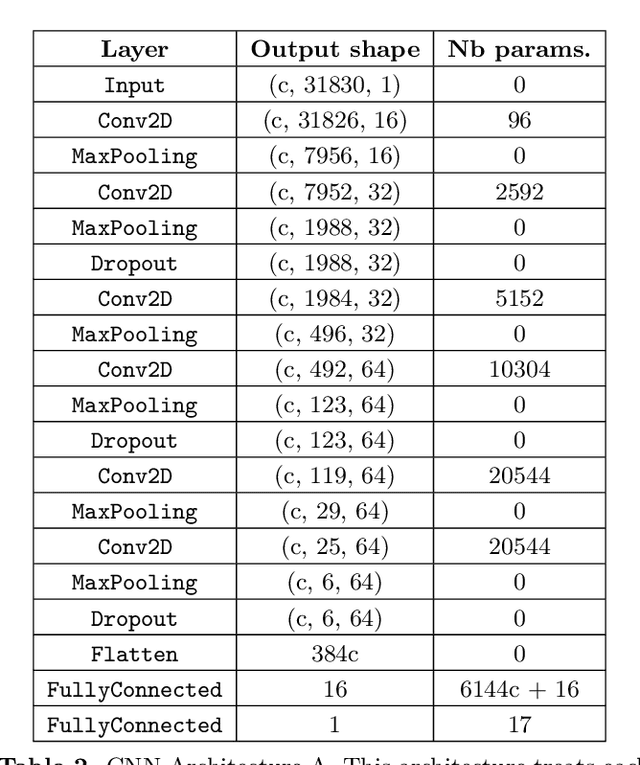
Understanding the long-term evolution of hierarchical triple systems is challenging due to its inherent chaotic nature, and it requires computationally expensive simulations. Here we propose a convolutional neural network model to predict the stability of hierarchical triples by looking at their evolution during the first $5 \times 10^5$ inner binary orbits. We employ the regularized few-body code \textsc{tsunami} to simulate $5\times 10^6$ hierarchical triples, from which we generate a large training and test dataset. We develop twelve different network configurations that use different combinations of the triples' orbital elements and compare their performances. Our best model uses 6 time-series, namely, the semimajor axes ratio, the inner and outer eccentricities, the mutual inclination and the arguments of pericenter. This model achieves an area under the curve of over $95\%$ and informs of the relevant parameters to study triple systems stability. All trained models are made publicly available, allowing to predict the stability of hierarchical triple systems $200$ times faster than pure $N$-body methods.