Cascaded channel modeling and experimental validation for RIS assisted communication system

Reconfigurable Intelligent Surface (RIS) is considered as a promising technology for 6G due to its ability to actively modify the electromagnetic propagation environment. Accurate channel modeling is essential for the design and evaluation of RIS assisted communication systems. Most current research models the RIS channel as a cascade of Tx-RIS and RIS-Rx sub-channels. However, most validation efforts regarding this assumption focus on large-scale path loss. To further explore this, in this paper, we derive and extend a convolution expression of RIS cascaded channel model based on the previously proposed Geometry-based Stochastic Model (GBSM)-based RIS cascaded channels. This model follows the 3GPP standard framework and leverages parameters such as angles, delays, and path powers defined in the GBSM model to more accurately reflect the smallscale characteristics of RIS multipath cascades. To verify the accuracy of this model, we conduct measurements of the TxRIS-Rx channel, Tx-RIS, and RIS-Rx sub-channels in a factory environment at 6.9 GHz, using the measured data to demonstrate the models validity and applicability in real-world scenarios. Validation with measured data shows that the proposed model accurately describes the characteristics of the RIS cascaded channel in terms of delay, angle, and power in complex multipath environments, providing important references for the design and deployment of RIS systems.

Learning to Prune Instances of Steiner Tree Problem in Graphs

We consider the Steiner tree problem on graphs where we are given a set of nodes and the goal is to find a tree sub-graph of minimum weight that contains all nodes in the given set, potentially including additional nodes. This is a classical NP-hard combinatorial optimisation problem. In recent years, a machine learning framework called learning-to-prune has been successfully used for solving a diverse range of combinatorial optimisation problems. In this paper, we use this learning framework on the Steiner tree problem and show that even on this problem, the learning-to-prune framework results in computing near-optimal solutions at a fraction of the time required by commercial ILP solvers. Our results underscore the potential of the learning-to-prune framework in solving various combinatorial optimisation problems.

Variational Autoencoder with CCA for Audio-Visual Cross-Modal Retrieval

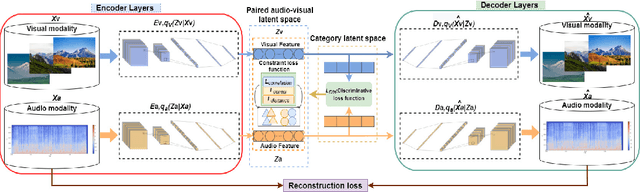
Cross-modal retrieval is to utilize one modality as a query to retrieve data from another modality, which has become a popular topic in information retrieval, machine learning, and database. How to effectively measure the similarity between different modality data is the major challenge of cross-modal retrieval. Although several reasearch works have calculated the correlation between different modality data via learning a common subspace representation, the encoder's ability to extract features from multi-modal information is not satisfactory. In this paper, we present a novel variational autoencoder (VAE) architecture for audio-visual cross-modal retrieval, by learning paired audio-visual correlation embedding and category correlation embedding as constraints to reinforce the mutuality of audio-visual information. On the one hand, audio encoder and visual encoder separately encode audio data and visual data into two different latent spaces. Further, two mutual latent spaces are respectively constructed by canonical correlation analysis (CCA). On the other hand, probabilistic modeling methods is used to deal with possible noise and missing information in the data. Additionally, in this way, the cross-modal discrepancy from intra-modal and inter-modal information are simultaneously eliminated in the joint embedding subspace. We conduct extensive experiments over two benchmark datasets. The experimental outcomes exhibit that the proposed architecture is effective in learning audio-visual correlation and is appreciably better than the existing cross-modal retrieval methods.

DL-AMP and DBTO: An Automatic Merge Planning and Trajectory Optimization and Its Application in Autonomous Driving

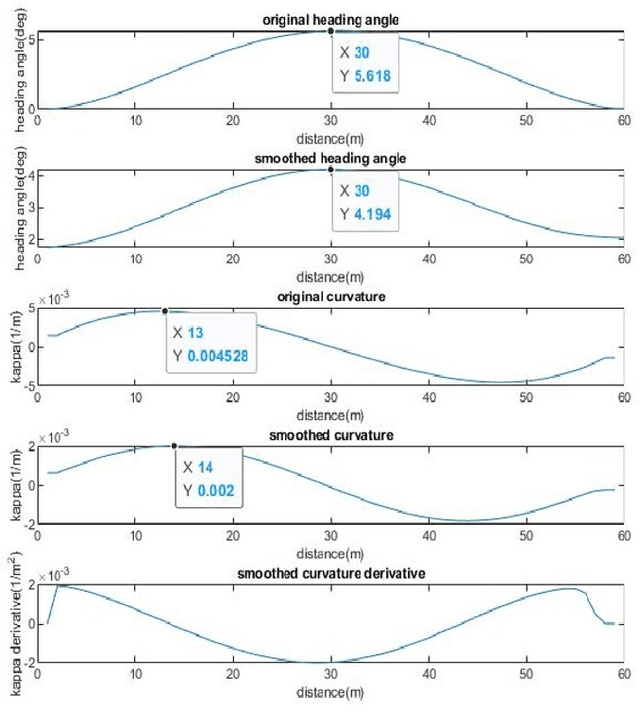
This paper presents an automatic merging algorithm for autonomous driving vehicles, which decouples the specific motion planning problem into a Dual-Layer Automatic Merge Planning (DL_AMP) and a Descent-Based Trajectory Optimization (DBTO). This work leads to great improvements in finding the best merge opportunity, lateral and longitudinal merge planning and control, trajectory postprocessing and driving comfort.

Frequency Principle in Deep Learning Beyond Gradient-descent-based Training

Frequency perspective recently makes progress in understanding deep learning. It has been widely verified in both empirical and theoretical studies that deep neural networks (DNNs) often fit the target function from low to high frequency, namely Frequency Principle (F-Principle). F-Principle sheds light on the strength and the weakness of DNNs and inspires a series of subsequent works, including theoretical studies, empirical studies and the design of efficient DNN structures etc. Previous works examine the F-Principle in gradient-descent-based training. It remains unclear whether gradient-descent-based training is a necessary condition for the F-Principle. In this paper, we show that the F-Principle exists stably in the training process of DNNs with non-gradient-descent-based training, including optimization algorithms with gradient information, such as conjugate gradient and BFGS, and algorithms without gradient information, such as Powell's method and Particle Swarm Optimization. These empirical studies show the universality of the F-Principle and provide hints for further study of F-Principle.

A priori generalization error for two-layer ReLU neural network through minimum norm solution

We focus on estimating \emph{a priori} generalization error of two-layer ReLU neural networks (NNs) trained by mean squared error, which only depends on initial parameters and the target function, through the following research line. We first estimate \emph{a priori} generalization error of finite-width two-layer ReLU NN with constraint of minimal norm solution, which is proved by \cite{zhang2019type} to be an equivalent solution of a linearized (w.r.t. parameter) finite-width two-layer NN. As the width goes to infinity, the linearized NN converges to the NN in Neural Tangent Kernel (NTK) regime \citep{jacot2018neural}. Thus, we can derive the \emph{a priori} generalization error of two-layer ReLU NN in NTK regime. The distance between NN in a NTK regime and a finite-width NN with gradient training is estimated by \cite{arora2019exact}. Based on the results in \cite{arora2019exact}, our work proves an \emph{a priori} generalization error bound of two-layer ReLU NNs. This estimate uses the intrinsic implicit bias of the minimum norm solution without requiring extra regularity in the loss function. This \emph{a priori} estimate also implies that NN does not suffer from curse of dimensionality, and a small generalization error can be achieved without requiring exponentially large number of neurons. In addition the research line proposed in this paper can also be used to study other properties of the finite-width network, such as the posterior generalization error.