ACDG-VTON: Accurate and Contained Diffusion Generation for Virtual Try-On

Virtual Try-on (VTON) involves generating images of a person wearing selected garments. Diffusion-based methods, in particular, can create high-quality images, but they struggle to maintain the identities of the input garments. We identified this problem stems from the specifics in the training formulation for diffusion. To address this, we propose a unique training scheme that limits the scope in which diffusion is trained. We use a control image that perfectly aligns with the target image during training. In turn, this accurately preserves garment details during inference. We demonstrate our method not only effectively conserves garment details but also allows for layering, styling, and shoe try-on. Our method runs multi-garment try-on in a single inference cycle and can support high-quality zoomed-in generations without training in higher resolutions. Finally, we show our method surpasses prior methods in accuracy and quality.

Me LLaMA: Foundation Large Language Models for Medical Applications

Recent large language models (LLMs) like ChatGPT and LLaMA have shown great promise in many AI applications. However, their performance on medical tasks is suboptimal and can be further improved by training on large domain-specific datasets. This study introduces Me LLaMA, a medical LLM family including foundation models - Me LLaMA 13/70B and their chat-enhanced versions - Me LLaMA 13/70B-chat, developed through the continual pre-training and instruction tuning of LLaMA2 using large medical data. Our domain-specific data suite for training and evaluation, includes a large-scale continual pre-training dataset with 129B tokens, an instruction tuning dataset with 214k samples, and a medical evaluation benchmark (MIBE) across six tasks with 14 datasets. Our extensive evaluation using MIBE shows that Me LLaMA models surpass existing open-source medical LLMs in zero-shot and few-shot learning and outperform commercial giants like ChatGPT on 6 out of 8 datasets and GPT-4 in 3 out of 8 datasets. In addition, we empirically investigated the catastrophic forgetting problem, and our results show that Me LLaMA models outperform other medical LLMs. Me LLaMA is one of the first and largest open-source foundational LLMs designed for the medical domain, using both biomedical and clinical data. It exhibits superior performance across both general and medical tasks compared to other medical LLMs, rendering it an attractive choice for medical AI applications. All resources are available at: https://github.com/BIDS-Xu-Lab/Me-LLaMA.

Preserving Image Properties Through Initializations in Diffusion Models

Retail photography imposes specific requirements on images. For instance, images may need uniform background colors, consistent model poses, centered products, and consistent lighting. Minor deviations from these standards impact a site's aesthetic appeal, making the images unsuitable for use. We show that Stable Diffusion methods, as currently applied, do not respect these requirements. The usual practice of training the denoiser with a very noisy image and starting inference with a sample of pure noise leads to inconsistent generated images during inference. This inconsistency occurs because it is easy to tell the difference between samples of the training and inference distributions. As a result, a network trained with centered retail product images with uniform backgrounds generates images with erratic backgrounds. The problem is easily fixed by initializing inference with samples from an approximation of noisy images. However, in using such an approximation, the joint distribution of text and noisy image at inference time still slightly differs from that at training time. This discrepancy is corrected by training the network with samples from the approximate noisy image distribution. Extensive experiments on real application data show significant qualitative and quantitative improvements in performance from adopting these procedures. Finally, our procedure can interact well with other control-based methods to further enhance the controllability of diffusion-based methods.

Higher-Order Newton Methods with Polynomial Work per Iteration

We present generalizations of Newton's method that incorporate derivatives of an arbitrary order $d$ but maintain a polynomial dependence on dimension in their cost per iteration. At each step, our $d^{\text{th}}$-order method uses semidefinite programming to construct and minimize a sum of squares-convex approximation to the $d^{\text{th}}$-order Taylor expansion of the function we wish to minimize. We prove that our $d^{\text{th}}$-order method has local convergence of order $d$. This results in lower oracle complexity compared to the classical Newton method. We show on numerical examples that basins of attraction around local minima can get larger as $d$ increases. Under additional assumptions, we present a modified algorithm, again with polynomial cost per iteration, which is globally convergent and has local convergence of order $d$.

Wearing the Same Outfit in Different Ways -- A Controllable Virtual Try-on Method

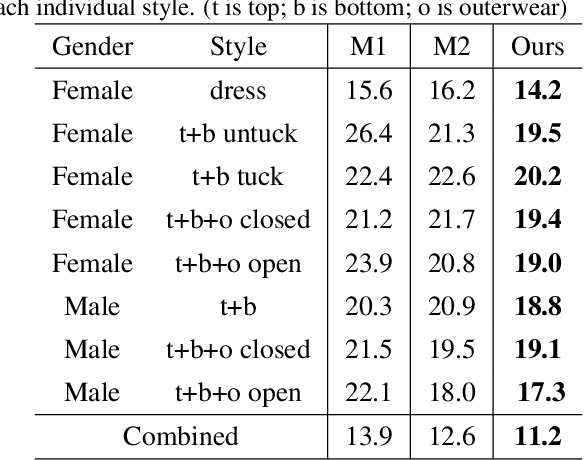
An outfit visualization method generates an image of a person wearing real garments from images of those garments. Current methods can produce images that look realistic and preserve garment identity, captured in details such as collar, cuffs, texture, hem, and sleeve length. However, no current method can both control how the garment is worn -- including tuck or untuck, opened or closed, high or low on the waist, etc.. -- and generate realistic images that accurately preserve the properties of the original garment. We describe an outfit visualization method that controls drape while preserving garment identity. Our system allows instance independent editing of garment drape, which means a user can construct an edit (e.g. tucking a shirt in a specific way) that can be applied to all shirts in a garment collection. Garment detail is preserved by relying on a warping procedure to place the garment on the body and a generator then supplies fine shading detail. To achieve instance independent control, we use control points with garment category-level semantics to guide the warp. The method produces state-of-the-art quality images, while allowing creative ways to style garments, including allowing tops to be tucked or untucked; jackets to be worn open or closed; skirts to be worn higher or lower on the waist; and so on. The method allows interactive control to correct errors in individual renderings too. Because the edits are instance independent, they can be applied to large pools of garments automatically and can be conditioned on garment metadata (e.g. all cropped jackets are worn closed or all bomber jackets are worn closed).

A Robot Cluster for Reproducible Research in Dexterous Manipulation

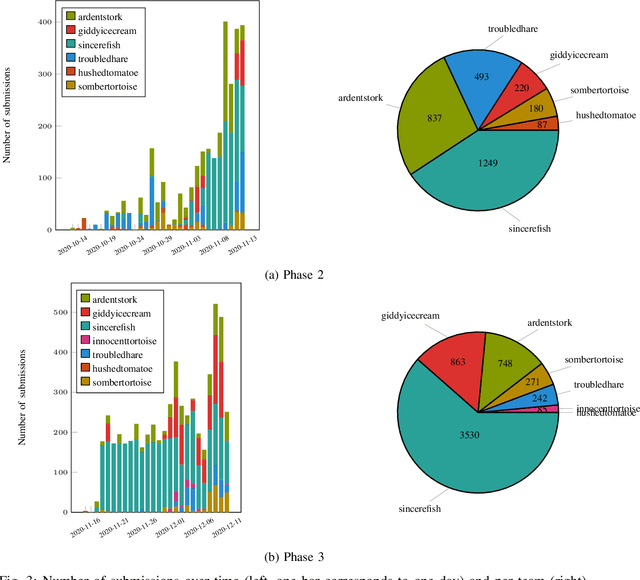
Dexterous manipulation remains an open problem in robotics. To coordinate efforts of the research community towards tackling this problem, we propose a shared benchmark. We designed and built robotic platforms that are hosted at the MPI-IS and can be accessed remotely. Each platform consists of three robotic fingers that are capable of dexterous object manipulation. Users are able to control the platforms remotely by submitting code that is executed automatically, akin to a computational cluster. Using this setup, i) we host robotics competitions, where teams from anywhere in the world access our platforms to tackle challenging tasks, ii) we publish the datasets collected during these competitions (consisting of hundreds of robot hours), and iii) we give researchers access to these platforms for their own projects.

Toward Accurate and Realistic Outfits Visualization with Attention to Details

Virtual try-on methods aim to generate images of fashion models wearing arbitrary combinations of garments. This is a challenging task because the generated image must appear realistic and accurately display the interaction between garments. Prior works produce images that are filled with artifacts and fail to capture important visual details necessary for commercial applications. We propose Outfit Visualization Net (OVNet) to capture these important details (e.g. buttons, shading, textures, realistic hemlines, and interactions between garments) and produce high quality multiple-garment virtual try-on images. OVNet consists of 1) a semantic layout generator and 2) an image generation pipeline using multiple coordinated warps. We train the warper to output multiple warps using a cascade loss, which refines each successive warp to focus on poorly generated regions of a previous warp and yields consistent improvements in detail. In addition, we introduce a method for matching outfits with the most suitable model and produce significant improvements for both our and other previous try-on methods. Through quantitative and qualitative analysis, we demonstrate our method generates substantially higher-quality studio images compared to prior works for multi-garment outfits. An interactive interface powered by this method has been deployed on fashion e-commerce websites and received overwhelmingly positive feedback.

Dexterous Manipulation Primitives for the Real Robot Challenge

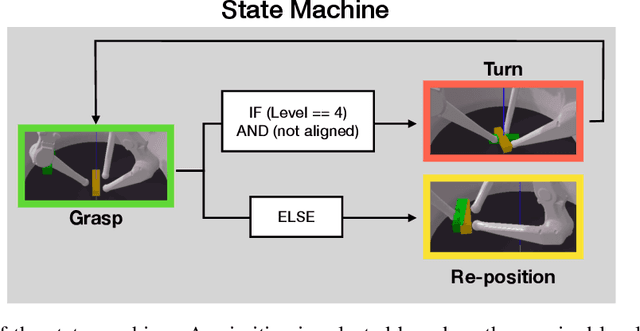
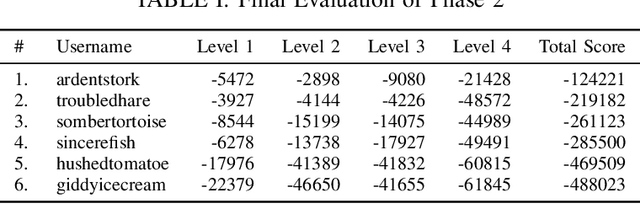
This report describes our approach for Phase 3 of the Real Robot Challenge. To solve cuboid manipulation tasks of varying difficulty, we decompose each task into the following primitives: moving the fingers to the cuboid to grasp it, turning it on the table to minimize orientation error, and re-positioning it to the goal position. We use model-based trajectory optimization and control to plan and execute these primitives. These grasping, turning, and re-positioning primitives are sequenced with a state-machine that determines which primitive to execute given the current object state and goal. Our method shows robust performance over multiple runs with randomized initial and goal positions. With this approach, our team placed second in the challenge, under the anonymous name "sombertortoise" on the leaderboard. Example runs of our method solving each of the four levels can be seen in this video (https://www.youtube.com/watch?v=I65Kwu9PGmg&list=PLt9QxrtaftrHGXcp4Oh8-s_OnQnBnLtei&index=1).

Complexity Aspects of Fundamental Questions in Polynomial Optimization

In this thesis, we settle the computational complexity of some fundamental questions in polynomial optimization. These include the questions of (i) finding a local minimum, (ii) testing local minimality of a point, and (iii) deciding attainment of the optimal value. Our results characterize the complexity of these three questions for all degrees of the defining polynomials left open by prior literature. Regarding (i) and (ii), we show that unless P=NP, there cannot be a polynomial-time algorithm that finds a point within Euclidean distance $c^n$ (for any constant $c$) of a local minimum of an $n$-variate quadratic program. By contrast, we show that a local minimum of a cubic polynomial can be found efficiently by semidefinite programming (SDP). We prove that second-order points of cubic polynomials admit an efficient semidefinite representation, even though their critical points are NP-hard to find. We also give an efficiently-checkable necessary and sufficient condition for local minimality of a point for a cubic polynomial. Regarding (iii), we prove that testing whether a quadratically constrained quadratic program with a finite optimal value has an optimal solution is NP-hard. We also show that testing coercivity of the objective function, compactness of the feasible set, and the Archimedean property associated with the description of the feasible set are all NP-hard. We also give a new characterization of coercive polynomials that lends itself to a hierarchy of SDPs. In our final chapter, we present an SDP relaxation for finding approximate Nash equilibria in bimatrix games. We show that for a symmetric game, a $1/3$-Nash equilibrium can be efficiently recovered from any rank-2 solution to this relaxation. We also propose SDP relaxations for NP-hard problems related to Nash equilibria, such as that of finding the highest achievable welfare under any Nash equilibrium.

On the complexity of finding a local minimizer of a quadratic function over a polytope

We show that unless P=NP, there cannot be a polynomial-time algorithm that finds a point within Euclidean distance $c^n$ (for any constant $c \ge 0$) of a local minimizer of an $n$-variate quadratic function over a polytope. This result (even with $c=0$) answers a question of Pardalos and Vavasis that appeared in 1992 on a list of seven open problems in complexity theory for numerical optimization. Our proof technique also implies that the problem of deciding whether a quadratic function has a local minimizer over an (unbounded) polyhedron, and that of deciding if a quartic polynomial has a local minimizer are NP-hard.