MagicDec: Breaking the Latency-Throughput Tradeoff for Long Context Generation with Speculative Decoding

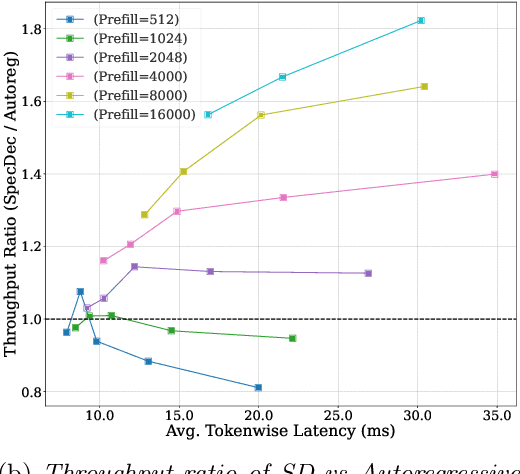
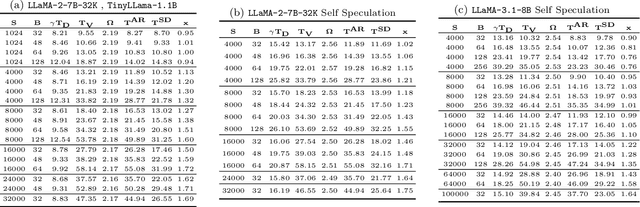
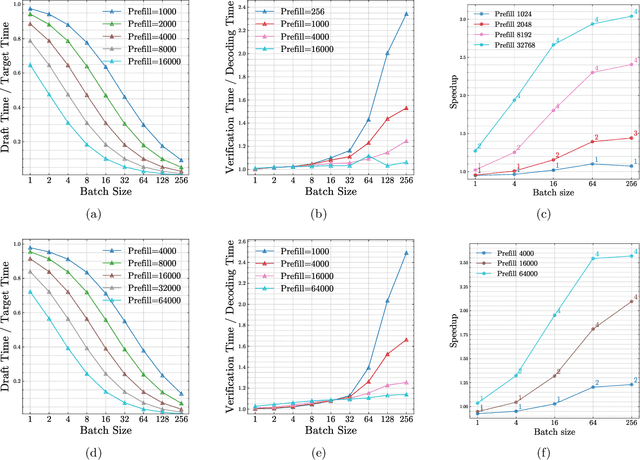
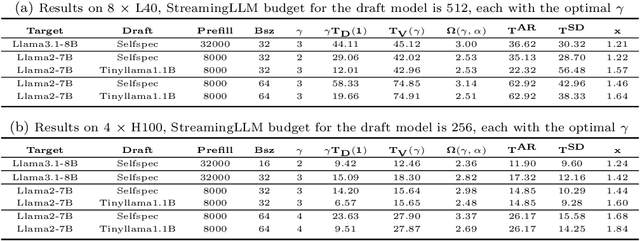
Large Language Models (LLMs) have become more prevalent in long-context applications such as interactive chatbots, document analysis, and agent workflows, but it is challenging to serve long-context requests with low latency and high throughput. Speculative decoding (SD) is a widely used technique to reduce latency without sacrificing performance but the conventional wisdom suggests that its efficacy is limited to small batch sizes. In MagicDec, we show that surprisingly SD can achieve speedup even for a high throughput inference regime for moderate to long sequences. More interestingly, an intelligent drafting strategy can achieve better speedup with increasing batch size based on our rigorous analysis. MagicDec first identifies the bottleneck shifts with increasing batch size and sequence length, and uses these insights to deploy speculative decoding more effectively for high throughput inference. Then, it leverages draft models with sparse KV cache to address the KV bottleneck that scales with both sequence length and batch size. This finding underscores the broad applicability of speculative decoding in long-context serving, as it can enhance throughput and reduce latency without compromising accuracy. For moderate to long sequences, we demonstrate up to 2x speedup for LLaMA-2-7B-32K and 1.84x speedup for LLaMA-3.1-8B when serving batch sizes ranging from 32 to 256 on 8 NVIDIA A100 GPUs. The code is available at https://github.com/Infini-AI-Lab/MagicDec/.

FP8-BERT: Post-Training Quantization for Transformer

Transformer-based models, such as BERT, have been widely applied in a wide range of natural language processing tasks. However, one inevitable side effect is that they require massive memory storage and inference cost when deployed in production. Quantization is one of the popularized ways to alleviate the cost. However, the previous 8-bit quantization strategy based on INT8 data format either suffers from the degradation of accuracy in a Post-Training Quantization (PTQ) fashion or requires an expensive Quantization-Aware Training (QAT) process. Recently, a new numeric format FP8 (i.e. floating-point of 8-bits) has been proposed and supported in commercial AI computing platforms such as H100. In this paper, we empirically validate the effectiveness of FP8 as a way to do Post-Training Quantization without significant loss of accuracy, with a simple calibration and format conversion process. We adopt the FP8 standard proposed by NVIDIA Corp. (2022) in our extensive experiments of BERT variants on GLUE and SQuAD v1.1 datasets, and show that PTQ with FP8 can significantly improve the accuracy upon that with INT8, to the extent of the full-precision model.

S4: a High-sparsity, High-performance AI Accelerator

Exploiting sparsity underlying neural networks has become one of the most potential methodologies to reduce the memory footprint, I/O cost, and computation workloads during inference. And the degree of sparsity one can exploit has become higher as larger model sizes have been considered along with the trend of pre-training giant models. On the other hand, compared with quantization that has been a widely supported option, acceleration through high-degree sparsity is not supported in most computing platforms. In this work, we introduce the first commercial hardware platform supporting high-degree sparsity acceleration up to 32 times -- S4. Combined with state-of-the-art sparse pruning techniques, we demonstrate several-times practical inference speedup on S4 over mainstream inference platforms such as Nvidia T4. We also show that in practice a sparse model of larger size can achieve both higher accuracy and higher throughput on S4 than a dense model of smaller size.

Efficient Global String Kernel with Random Features: Beyond Counting Substructures

Analysis of large-scale sequential data has been one of the most crucial tasks in areas such as bioinformatics, text, and audio mining. Existing string kernels, however, either (i) rely on local features of short substructures in the string, which hardly capture long discriminative patterns, (ii) sum over too many substructures, such as all possible subsequences, which leads to diagonal dominance of the kernel matrix, or (iii) rely on non-positive-definite similarity measures derived from the edit distance. Furthermore, while there have been works addressing the computational challenge with respect to the length of string, most of them still experience quadratic complexity in terms of the number of training samples when used in a kernel-based classifier. In this paper, we present a new class of global string kernels that aims to (i) discover global properties hidden in the strings through global alignments, (ii) maintain positive-definiteness of the kernel, without introducing a diagonal dominant kernel matrix, and (iii) have a training cost linear with respect to not only the length of the string but also the number of training string samples. To this end, the proposed kernels are explicitly defined through a series of different random feature maps, each corresponding to a distribution of random strings. We show that kernels defined this way are always positive-definite, and exhibit computational benefits as they always produce \emph{Random String Embeddings (RSE)} that can be directly used in any linear classification models. Our extensive experiments on nine benchmark datasets corroborate that RSE achieves better or comparable accuracy in comparison to state-of-the-art baselines, especially with the strings of longer lengths. In addition, we empirically show that RSE scales linearly with the increase of the number and the length of string.

Scalable Global Alignment Graph Kernel Using Random Features: From Node Embedding to Graph Embedding

Graph kernels are widely used for measuring the similarity between graphs. Many existing graph kernels, which focus on local patterns within graphs rather than their global properties, suffer from significant structure information loss when representing graphs. Some recent global graph kernels, which utilizes the alignment of geometric node embeddings of graphs, yield state-of-the-art performance. However, these graph kernels are not necessarily positive-definite. More importantly, computing the graph kernel matrix will have at least quadratic {time} complexity in terms of the number and the size of the graphs. In this paper, we propose a new family of global alignment graph kernels, which take into account the global properties of graphs by using geometric node embeddings and an associated node transportation based on earth mover's distance. Compared to existing global kernels, the proposed kernel is positive-definite. Our graph kernel is obtained by defining a distribution over \emph{random graphs}, which can naturally yield random feature approximations. The random feature approximations lead to our graph embeddings, which is named as "random graph embeddings" (RGE). In particular, RGE is shown to achieve \emph{(quasi-)linear scalability} with respect to the number and the size of the graphs. The experimental results on nine benchmark datasets demonstrate that RGE outperforms or matches twelve state-of-the-art graph classification algorithms.

Random Warping Series: A Random Features Method for Time-Series Embedding

Time series data analytics has been a problem of substantial interests for decades, and Dynamic Time Warping (DTW) has been the most widely adopted technique to measure dissimilarity between time series. A number of global-alignment kernels have since been proposed in the spirit of DTW to extend its use to kernel-based estimation method such as support vector machine. However, those kernels suffer from diagonal dominance of the Gram matrix and a quadratic complexity w.r.t. the sample size. In this work, we study a family of alignment-aware positive definite (p.d.) kernels, with its feature embedding given by a distribution of \emph{Random Warping Series (RWS)}. The proposed kernel does not suffer from the issue of diagonal dominance while naturally enjoys a \emph{Random Features} (RF) approximation, which reduces the computational complexity of existing DTW-based techniques from quadratic to linear in terms of both the number and the length of time-series. We also study the convergence of the RF approximation for the domain of time series of unbounded length. Our extensive experiments on 16 benchmark datasets demonstrate that RWS outperforms or matches state-of-the-art classification and clustering methods in both accuracy and computational time. Our code and data is available at { \url{https://github.com/IBM/RandomWarpingSeries}}.

Scalable Spectral Clustering Using Random Binning Features

Spectral clustering is one of the most effective clustering approaches that capture hidden cluster structures in the data. However, it does not scale well to large-scale problems due to its quadratic complexity in constructing similarity graphs and computing subsequent eigendecomposition. Although a number of methods have been proposed to accelerate spectral clustering, most of them compromise considerable information loss in the original data for reducing computational bottlenecks. In this paper, we present a novel scalable spectral clustering method using Random Binning features (RB) to simultaneously accelerate both similarity graph construction and the eigendecomposition. Specifically, we implicitly approximate the graph similarity (kernel) matrix by the inner product of a large sparse feature matrix generated by RB. Then we introduce a state-of-the-art SVD solver to effectively compute eigenvectors of this large matrix for spectral clustering. Using these two building blocks, we reduce the computational cost from quadratic to linear in the number of data points while achieving similar accuracy. Our theoretical analysis shows that spectral clustering via RB converges faster to the exact spectral clustering than the standard Random Feature approximation. Extensive experiments on 8 benchmarks show that the proposed method either outperforms or matches the state-of-the-art methods in both accuracy and runtime. Moreover, our method exhibits linear scalability in both the number of data samples and the number of RB features.

D2KE: From Distance to Kernel and Embedding

For many machine learning problem settings, particularly with structured inputs such as sequences or sets of objects, a distance measure between inputs can be specified more naturally than a feature representation. However, most standard machine models are designed for inputs with a vector feature representation. In this work, we consider the estimation of a function $f:\mathcal{X} \rightarrow \R$ based solely on a dissimilarity measure $d:\mathcal{X}\times\mathcal{X} \rightarrow \R$ between inputs. In particular, we propose a general framework to derive a family of \emph{positive definite kernels} from a given dissimilarity measure, which subsumes the widely-used \emph{representative-set method} as a special case, and relates to the well-known \emph{distance substitution kernel} in a limiting case. We show that functions in the corresponding Reproducing Kernel Hilbert Space (RKHS) are Lipschitz-continuous w.r.t. the given distance metric. We provide a tractable algorithm to estimate a function from this RKHS, and show that it enjoys better generalizability than Nearest-Neighbor estimates. Our approach draws from the literature of Random Features, but instead of deriving feature maps from an existing kernel, we construct novel kernels from a random feature map, that we specify given the distance measure. We conduct classification experiments with such disparate domains as strings, time series, and sets of vectors, where our proposed framework compares favorably to existing distance-based learning methods such as $k$-nearest-neighbors, distance-substitution kernels, pseudo-Euclidean embedding, and the representative-set method.