XL3M: A Training-free Framework for LLM Length Extension Based on Segment-wise Inference

Length generalization failure problem, namely the large language model (LLM) fails to generalize to texts longer than its maximum training length, greatly restricts the application of LLM in the scenarios with streaming long inputs. To address this problem, the existing methods either require substantial costs or introduce precision loss. In this paper, we empirically find that the accuracy of the LLM's prediction is highly correlated to its certainty. Based on this, we propose an efficient training free framework, named XL3M (it means extra-long large language model), which enables the LLMs trained on short sequences to reason extremely long sequence without any further training or fine-tuning. Under the XL3M framework, the input context will be firstly decomposed into multiple short sub-contexts, where each sub-context contains an independent segment and a common ``question'' which is a few tokens from the end of the original context. Then XL3M gives a method to measure the relevance between each segment and the ``question'', and constructs a concise key context by splicing all the relevant segments in chronological order. The key context is further used instead of the original context to complete the inference task. Evaluations on comprehensive benchmarks show the superiority of XL3M. Using our framework, a Llama2-7B model is able to reason 20M long sequences on an 8-card Huawei Ascend 910B NPU machine with 64GB memory per card.

One for Multiple: Physics-informed Synthetic Data Boosts Generalizable Deep Learning for Fast MRI Reconstruction

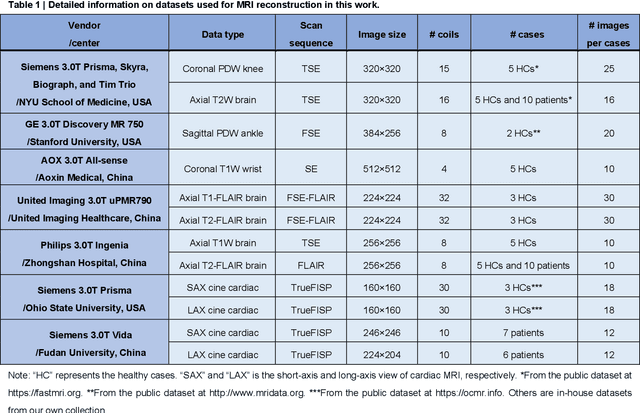
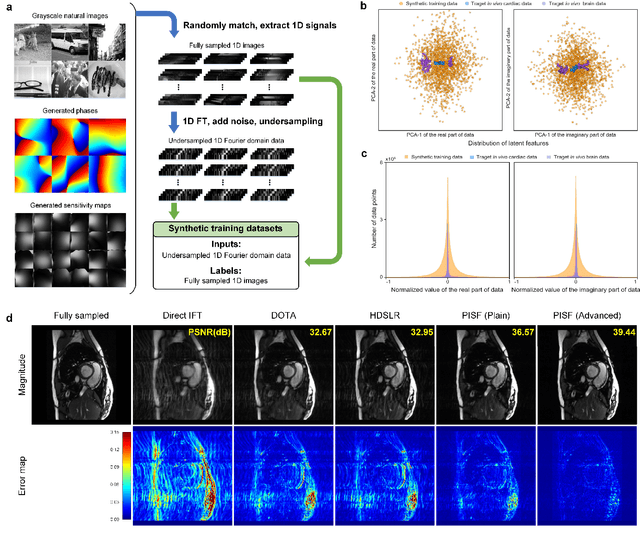
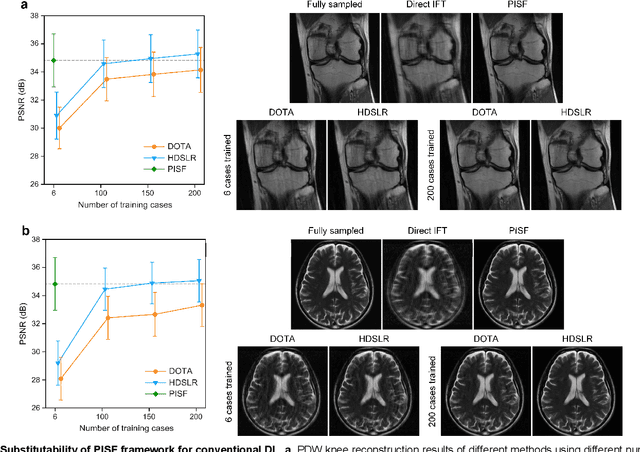
Magnetic resonance imaging (MRI) is a principal radiological modality that provides radiation-free, abundant, and diverse information about the whole human body for medical diagnosis, but suffers from prolonged scan time. The scan time can be significantly reduced through k-space undersampling but the introduced artifacts need to be removed in image reconstruction. Although deep learning (DL) has emerged as a powerful tool for image reconstruction in fast MRI, its potential in multiple imaging scenarios remains largely untapped. This is because not only collecting large-scale and diverse realistic training data is generally costly and privacy-restricted, but also existing DL methods are hard to handle the practically inevitable mismatch between training and target data. Here, we present a Physics-Informed Synthetic data learning framework for Fast MRI, called PISF, which is the first to enable generalizable DL for multi-scenario MRI reconstruction using solely one trained model. For a 2D image, the reconstruction is separated into many 1D basic problems and starts with the 1D data synthesis, to facilitate generalization. We demonstrate that training DL models on synthetic data, integrated with enhanced learning techniques, can achieve comparable or even better in vivo MRI reconstruction compared to models trained on a matched realistic dataset, reducing the demand for real-world MRI data by up to 96%. Moreover, our PISF shows impressive generalizability in multi-vendor multi-center imaging. Its excellent adaptability to patients has been verified through 10 experienced doctors' evaluations. PISF provides a feasible and cost-effective way to markedly boost the widespread usage of DL in various fast MRI applications, while freeing from the intractable ethical and practical considerations of in vivo human data acquisitions.

One-dimensional Deep Low-rank and Sparse Network for Accelerated MRI

Deep learning has shown astonishing performance in accelerated magnetic resonance imaging (MRI). Most state-of-the-art deep learning reconstructions adopt the powerful convolutional neural network and perform 2D convolution since many magnetic resonance images or their corresponding k-space are in 2D. In this work, we present a new approach that explores the 1D convolution, making the deep network much easier to be trained and generalized. We further integrate the 1D convolution into the proposed deep network, named as One-dimensional Deep Low-rank and Sparse network (ODLS), which unrolls the iteration procedure of a low-rank and sparse reconstruction model. Extensive results on in vivo knee and brain datasets demonstrate that, the proposed ODLS is very suitable for the case of limited training subjects and provides improved reconstruction performance than state-of-the-art methods both visually and quantitatively. Additionally, ODLS also shows nice robustness to different undersampling scenarios and some mismatches between the training and test data. In summary, our work demonstrates that the 1D deep learning scheme is memory-efficient and robust in fast MRI.

Optimal Rates of Distributed Regression with Imperfect Kernels

Distributed machine learning systems have been receiving increasing attentions for their efficiency to process large scale data. Many distributed frameworks have been proposed for different machine learning tasks. In this paper, we study the distributed kernel regression via the divide and conquer approach. This approach has been proved asymptotically minimax optimal if the kernel is perfectly selected so that the true regression function lies in the associated reproducing kernel Hilbert space. However, this is usually, if not always, impractical because kernels that can only be selected via prior knowledge or a tuning process are hardly perfect. Instead it is more common that the kernel is good enough but imperfect in the sense that the true regression can be well approximated by but does not lie exactly in the kernel space. We show distributed kernel regression can still achieves capacity independent optimal rate in this case. To this end, we first establish a general framework that allows to analyze distributed regression with response weighted base algorithms by bounding the error of such algorithms on a single data set, provided that the error bounds has factored the impact of the unexplained variance of the response variable. Then we perform a leave one out analysis of the kernel ridge regression and bias corrected kernel ridge regression, which in combination with the aforementioned framework allows us to derive sharp error bounds and capacity independent optimal rates for the associated distributed kernel regression algorithms. As a byproduct of the thorough analysis, we also prove the kernel ridge regression can achieve rates faster than $N^{-1}$ (where $N$ is the sample size) in the noise free setting which, to our best knowledge, are first observed and novel in regression learning.