Dongkun Zhang
CarPlanner: Consistent Auto-regressive Trajectory Planning for Large-scale Reinforcement Learning in Autonomous Driving
Feb 27, 2025Abstract:Trajectory planning is vital for autonomous driving, ensuring safe and efficient navigation in complex environments. While recent learning-based methods, particularly reinforcement learning (RL), have shown promise in specific scenarios, RL planners struggle with training inefficiencies and managing large-scale, real-world driving scenarios. In this paper, we introduce \textbf{CarPlanner}, a \textbf{C}onsistent \textbf{a}uto-\textbf{r}egressive \textbf{Planner} that uses RL to generate multi-modal trajectories. The auto-regressive structure enables efficient large-scale RL training, while the incorporation of consistency ensures stable policy learning by maintaining coherent temporal consistency across time steps. Moreover, CarPlanner employs a generation-selection framework with an expert-guided reward function and an invariant-view module, simplifying RL training and enhancing policy performance. Extensive analysis demonstrates that our proposed RL framework effectively addresses the challenges of training efficiency and performance enhancement, positioning CarPlanner as a promising solution for trajectory planning in autonomous driving. To the best of our knowledge, we are the first to demonstrate that the RL-based planner can surpass both IL- and rule-based state-of-the-arts (SOTAs) on the challenging large-scale real-world dataset nuPlan. Our proposed CarPlanner surpasses RL-, IL-, and rule-based SOTA approaches within this demanding dataset.
A Two-stage Based Social Preference Recognition in Multi-Agent Autonomous Driving System
Oct 05, 2023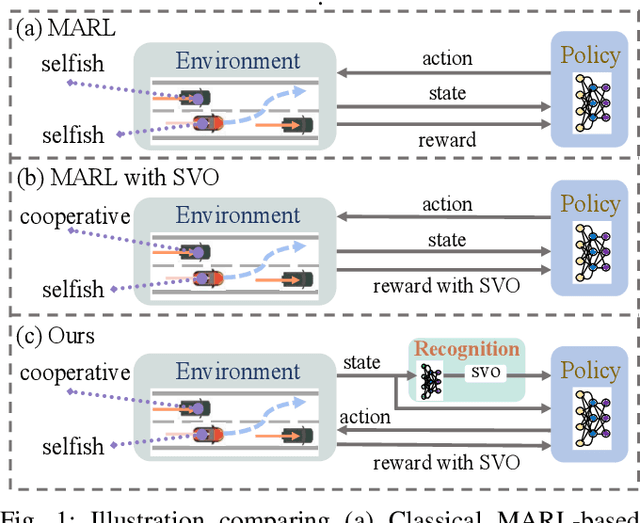
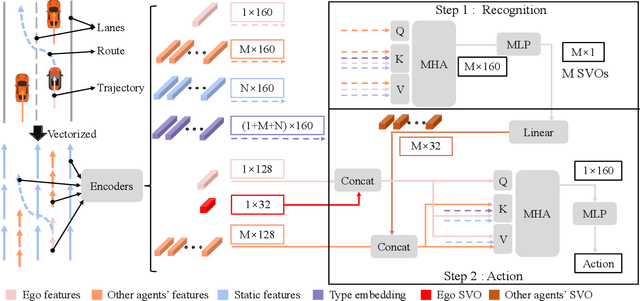
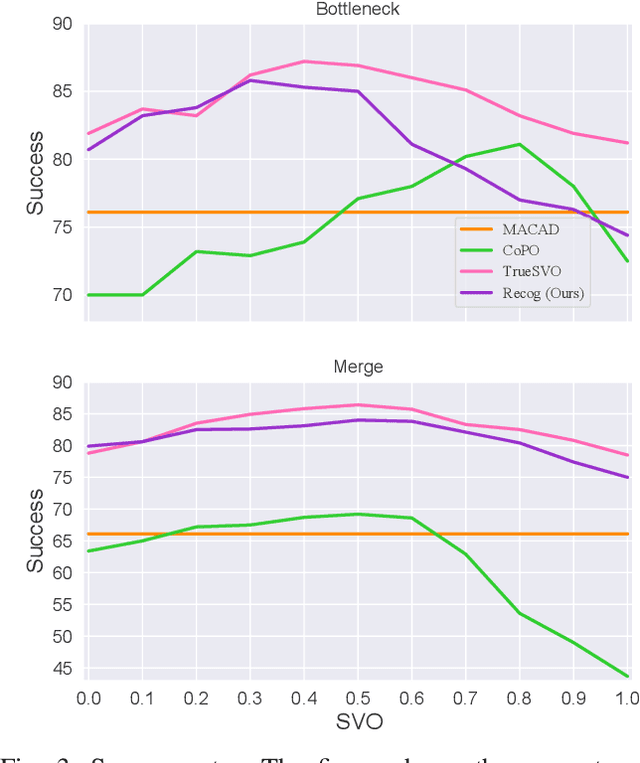
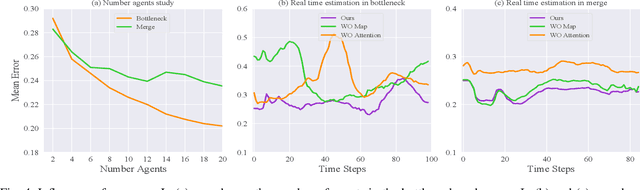
Abstract:Multi-Agent Reinforcement Learning (MARL) has become a promising solution for constructing a multi-agent autonomous driving system (MADS) in complex and dense scenarios. But most methods consider agents acting selfishly, which leads to conflict behaviors. Some existing works incorporate the concept of social value orientation (SVO) to promote coordination, but they lack the knowledge of other agents' SVOs, resulting in conservative maneuvers. In this paper, we aim to tackle the mentioned problem by enabling the agents to understand other agents' SVOs. To accomplish this, we propose a two-stage system framework. Firstly, we train a policy by allowing the agents to share their ground truth SVOs to establish a coordinated traffic flow. Secondly, we develop a recognition network that estimates agents' SVOs and integrates it with the policy trained in the first stage. Experiments demonstrate that our developed method significantly improves the performance of the driving policy in MADS compared to two state-of-the-art MARL algorithms.
Zero-shot Transfer Learning of Driving Policy via Socially Adversarial Traffic Flow
Apr 25, 2023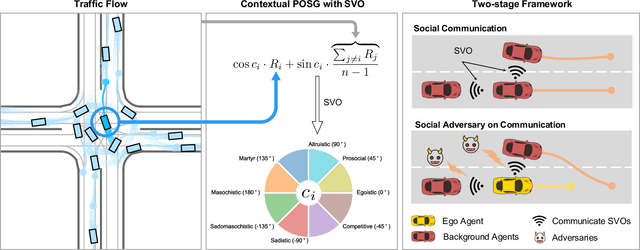
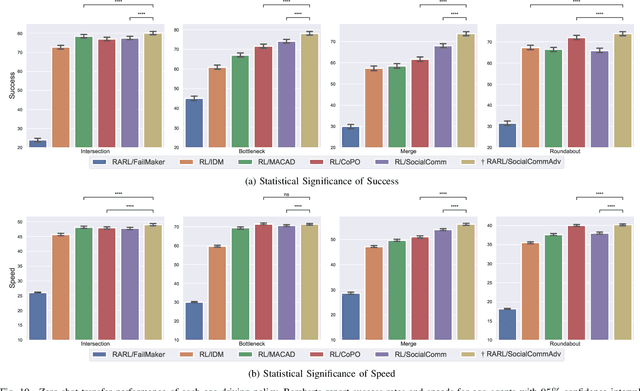
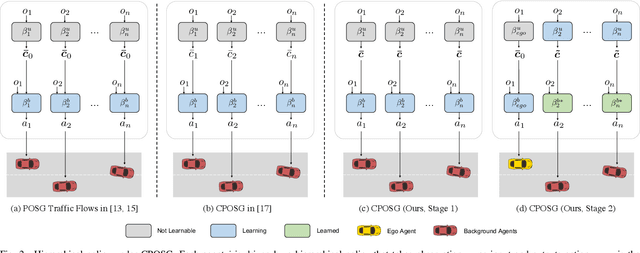
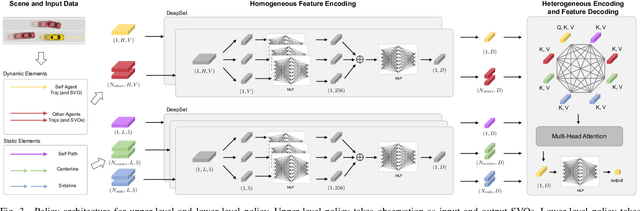
Abstract:Acquiring driving policies that can transfer to unseen environments is challenging when driving in dense traffic flows. The design of traffic flow is essential and previous studies are unable to balance interaction and safety-criticism. To tackle this problem, we propose a socially adversarial traffic flow. We propose a Contextual Partially-Observable Stochastic Game to model traffic flow and assign Social Value Orientation (SVO) as context. We then adopt a two-stage framework. In Stage 1, each agent in our socially-aware traffic flow is driven by a hierarchical policy where upper-level policy communicates genuine SVOs of all agents, which the lower-level policy takes as input. In Stage 2, each agent in the socially adversarial traffic flow is driven by the hierarchical policy where upper-level communicates mistaken SVOs, taken by the lower-level policy trained in Stage 1. Driving policy is adversarially trained through a zero-sum game formulation with upper-level policies, resulting in a policy with enhanced zero-shot transfer capability to unseen traffic flows. Comprehensive experiments on cross-validation verify the superior zero-shot transfer performance of our method.
Domain Generalization for Vision-based Driving Trajectory Generation
Sep 22, 2021
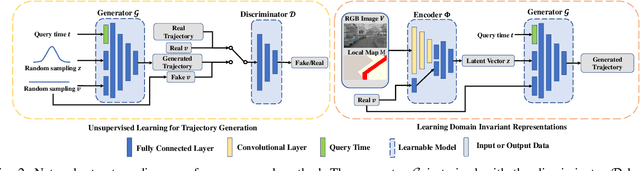
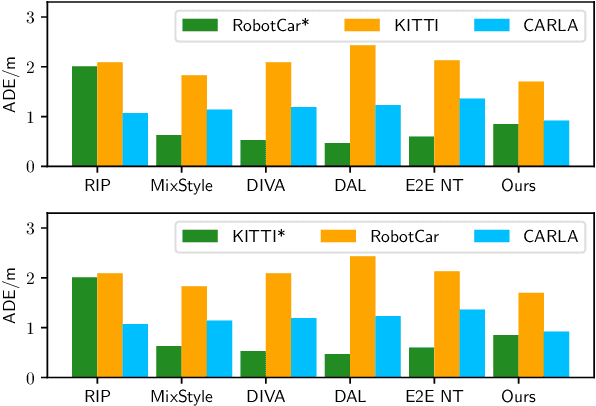

Abstract:One of the challenges in vision-based driving trajectory generation is dealing with out-of-distribution scenarios. In this paper, we propose a domain generalization method for vision-based driving trajectory generation for autonomous vehicles in urban environments, which can be seen as a solution to extend the Invariant Risk Minimization (IRM) method in complex problems. We leverage an adversarial learning approach to train a trajectory generator as the decoder. Based on the pre-trained decoder, we infer the latent variables corresponding to the trajectories, and pre-train the encoder by regressing the inferred latent variable. Finally, we fix the decoder but fine-tune the encoder with the final trajectory loss. We compare our proposed method with the state-of-the-art trajectory generation method and some recent domain generalization methods on both datasets and simulation, demonstrating that our method has better generalization ability.
Learning Observation-Based Certifiable Safe Policy for Decentralized Multi-Robot Navigation
Sep 16, 2021



Abstract:Safety is of great importance in multi-robot navigation problems. In this paper, we propose a control barrier function (CBF) based optimizer that ensures robot safety with both high probability and flexibility, using only sensor measurement. The optimizer takes action commands from the policy network as initial values and then provides refinement to drive the potentially dangerous ones back into safe regions. With the help of a deep transition model that predicts the evolution of surrounding dynamics and the consequences of different actions, the CBF module can guide the optimization in a reasonable time horizon. We also present a novel joint training framework that improves the cooperation between the Reinforcement Learning (RL) based policy and the CBF-based optimizer both in training and inference procedures by utilizing reward feedback from the CBF module. We observe that the policy using our method can achieve a higher success rate while maintaining the safety of multiple robots in significantly fewer episodes compared with other methods. Experiments are conducted in multiple scenarios both in simulation and the real world, the results demonstrate the effectiveness of our method in maintaining the safety of multi-robot navigation. Code is available at \url{https://github.com/YuxiangCui/MARL-OCBF
Imitation Learning of Hierarchical Driving Model: from Continuous Intention to Continuous Trajectory
Oct 20, 2020



Abstract:One of the challenges to reduce the gap between the machine and the human level driving is how to endow the system with the learning capacity to deal with the coupled complexity of environments, intentions, and dynamics. In this paper, we propose a hierarchical driving model with explicit model of continuous intention and continuous dynamics, which decouples the complexity in the observation-to-action reasoning in the human driving data. Specifically, the continuous intention module takes the route planning and perception to generate a potential map encoded with obstacles and goals being expressed as grid based potentials. Then, the potential map is regarded as a condition, together with the current dynamics, to generate the trajectory. The trajectory is modeled by a network based continuous function approximator, which naturally reserves the derivatives for high-order supervision without any additional parameters. Finally, we validate our method on both datasets and simulators, demonstrating superior performance. The method is also deployed on the real vehicle with loop latency, validating its effectiveness.
Learning hierarchical behavior and motion planning for autonomous driving
May 08, 2020
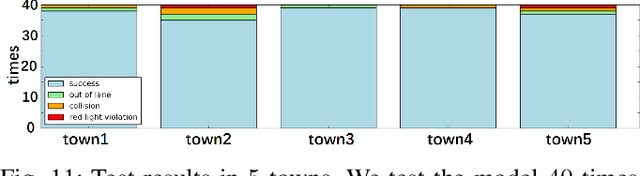

Abstract:Learning-based driving solution, a new branch for autonomous driving, is expected to simplify the modeling of driving by learning the underlying mechanisms from data. To improve the tactical decision-making for learning-based driving solution, we introduce hierarchical behavior and motion planning (HBMP) to explicitly model the behavior in learning-based solution. Due to the coupled action space of behavior and motion, it is challenging to solve HBMP problem using reinforcement learning (RL) for long-horizon driving tasks. We transform HBMP problem by integrating a classical sampling-based motion planner, of which the optimal cost is regarded as the rewards for high-level behavior learning. As a result, this formulation reduces action space and diversifies the rewards without losing the optimality of HBMP. In addition, we propose a sharable representation for input sensory data across simulation platforms and real-world environment, so that models trained in a fast event-based simulator, SUMO, can be used to initialize and accelerate the RL training in a dynamics based simulator, CARLA. Experimental results demonstrate the effectiveness of the method. Besides, the model is successfully transferred to the real-world, validating the generalization capability.
PPINN: Parareal Physics-Informed Neural Network for time-dependent PDEs
Sep 23, 2019



Abstract:Physics-informed neural networks (PINNs) encode physical conservation laws and prior physical knowledge into the neural networks, ensuring the correct physics is represented accurately while alleviating the need for supervised learning to a great degree. While effective for relatively short-term time integration, when long time integration of the time-dependent PDEs is sought, the time-space domain may become arbitrarily large and hence training of the neural network may become prohibitively expensive. To this end, we develop a parareal physics-informed neural network (PPINN), hence decomposing a long-time problem into many independent short-time problems supervised by an inexpensive/fast coarse-grained (CG) solver. In particular, the serial CG solver is designed to provide approximate predictions of the solution at discrete times, while initiate many fine PINNs simultaneously to correct the solution iteratively. There is a two-fold benefit from training PINNs with small-data sets rather than working on a large-data set directly, i.e., training of individual PINNs with small-data is much faster, while training the fine PINNs can be readily parallelized. Consequently, compared to the original PINN approach, the proposed PPINN approach may achieve a significant speedup for long-time integration of PDEs, assuming that the CG solver is fast and can provide reasonable predictions of the solution, hence aiding the PPINN solution to converge in just a few iterations. To investigate the PPINN performance on solving time-dependent PDEs, we first apply the PPINN to solve the Burgers equation, and subsequently we apply the PPINN to solve a two-dimensional nonlinear diffusion-reaction equation. Our results demonstrate that PPINNs converge in a couple of iterations with significant speed-ups proportional to the number of time-subdomains employed.
Learning in Modal Space: Solving Time-Dependent Stochastic PDEs Using Physics-Informed Neural Networks
May 03, 2019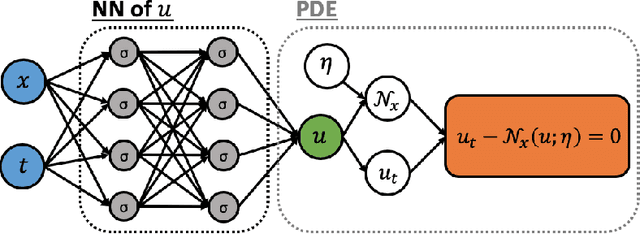
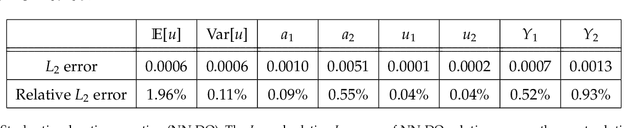
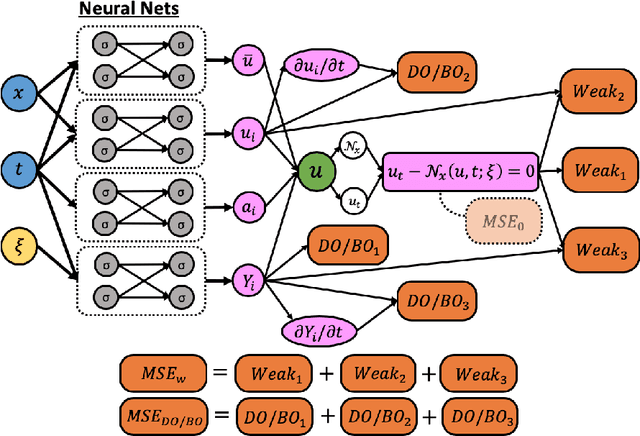

Abstract:One of the open problems in scientific computing is the long-time integration of nonlinear stochastic partial differential equations (SPDEs). We address this problem by taking advantage of recent advances in scientific machine learning and the dynamically orthogonal (DO) and bi-orthogonal (BO) methods for representing stochastic processes. Specifically, we propose two new Physics-Informed Neural Networks (PINNs) for solving time-dependent SPDEs, namely the NN-DO/BO methods, which incorporate the DO/BO constraints into the loss function with an implicit form instead of generating explicit expressions for the temporal derivatives of the DO/BO modes. Hence, the proposed methods overcome some of the drawbacks of the original DO/BO methods: we do not need the assumption that the covariance matrix of the random coefficients is invertible as in the original DO method, and we can remove the assumption of no eigenvalue crossing as in the original BO method. Moreover, the NN-DO/BO methods can be used to solve time-dependent stochastic inverse problems with the same formulation and computational complexity as for forward problems. We demonstrate the capability of the proposed methods via several numerical examples: (1) A linear stochastic advection equation with deterministic initial condition where the original DO/BO method would fail; (2) Long-time integration of the stochastic Burgers' equation with many eigenvalue crossings during the whole time evolution where the original BO method fails. (3) Nonlinear reaction diffusion equation: we consider both the forward and the inverse problem, including noisy initial data, to investigate the flexibility of the NN-DO/BO methods in handling inverse and mixed type problems. Taken together, these simulation results demonstrate that the NN-DO/BO methods can be employed to effectively quantify uncertainty propagation in a wide range of physical problems.
Physics-Informed Generative Adversarial Networks for Stochastic Differential Equations
Nov 05, 2018



Abstract:We developed a new class of physics-informed generative adversarial networks (PI-GANs) to solve in a unified manner forward, inverse and mixed stochastic problems based on a limited number of scattered measurements. Unlike standard GANs relying only on data for training, here we encoded into the architecture of GANs the governing physical laws in the form of stochastic differential equations (SDEs) using automatic differentiation. In particular, we applied Wasserstein GANs with gradient penalty (WGAN-GP) for its enhanced stability compared to vanilla GANs. We first tested WGAN-GP in approximating Gaussian processes of different correlation lengths based on data realizations collected from simultaneous reads at sparsely placed sensors. We obtained good approximation of the generated stochastic processes to the target ones even for a mismatch between the input noise dimensionality and the effective dimensionality of the target stochastic processes. We also studied the overfitting issue for both the discriminator and generator, and we found that overfitting occurs also in the generator in addition to the discriminator as previously reported. Subsequently, we considered the solution of elliptic SDEs requiring approximations of three stochastic processes, namely the solution, the forcing, and the diffusion coefficient. We used three generators for the PI-GANs, two of them were feed forward deep neural networks (DNNs) while the other one was the neural network induced by the SDE. Depending on the data, we employed one or multiple feed forward DNNs as the discriminators in PI-GANs. Here, we have demonstrated the accuracy and effectiveness of PI-GANs in solving SDEs for up to 30 dimensions, but in principle, PI-GANs could tackle very high dimensional problems given more sensor data with low-polynomial growth in computational cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge