Differentiating Policies for Non-Myopic Bayesian Optimization

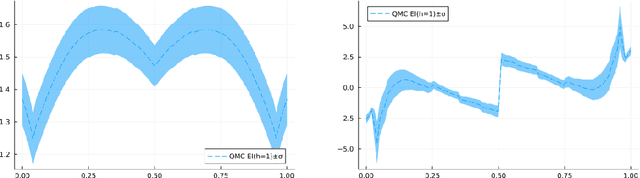
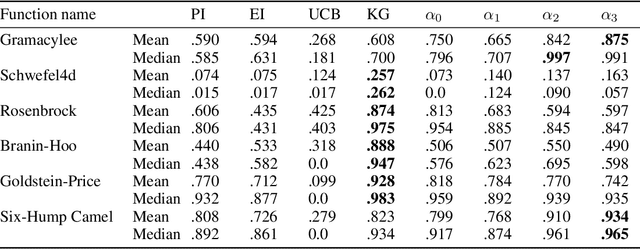
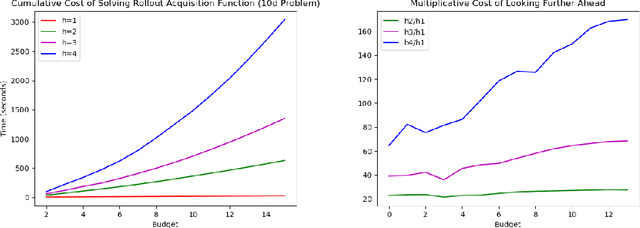
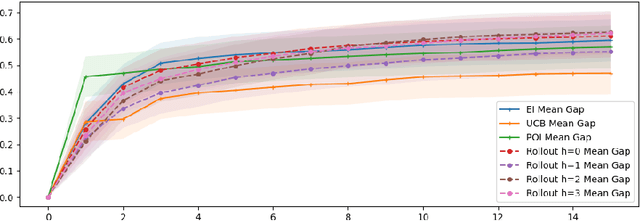
Bayesian optimization (BO) methods choose sample points by optimizing an acquisition function derived from a statistical model of the objective. These acquisition functions are chosen to balance sampling regions with predicted good objective values against exploring regions where the objective is uncertain. Standard acquisition functions are myopic, considering only the impact of the next sample, but non-myopic acquisition functions may be more effective. In principle, one could model the sampling by a Markov decision process, and optimally choose the next sample by maximizing an expected reward computed by dynamic programming; however, this is infeasibly expensive. More practical approaches, such as rollout, consider a parametric family of sampling policies. In this paper, we show how to efficiently estimate rollout acquisition functions and their gradients, enabling stochastic gradient-based optimization of sampling policies.

On-the-Fly Rectification for Robust Large-Vocabulary Topic Inference

Across many data domains, co-occurrence statistics about the joint appearance of objects are powerfully informative. By transforming unsupervised learning problems into decompositions of co-occurrence statistics, spectral algorithms provide transparent and efficient algorithms for posterior inference such as latent topic analysis and community detection. As object vocabularies grow, however, it becomes rapidly more expensive to store and run inference algorithms on co-occurrence statistics. Rectifying co-occurrence, the key process to uphold model assumptions, becomes increasingly more vital in the presence of rare terms, but current techniques cannot scale to large vocabularies. We propose novel methods that simultaneously compress and rectify co-occurrence statistics, scaling gracefully with the size of vocabulary and the dimension of latent space. We also present new algorithms learning latent variables from the compressed statistics, and verify that our methods perform comparably to previous approaches on both textual and non-textual data.

Surveillance Evasion Through Bayesian Reinforcement Learning

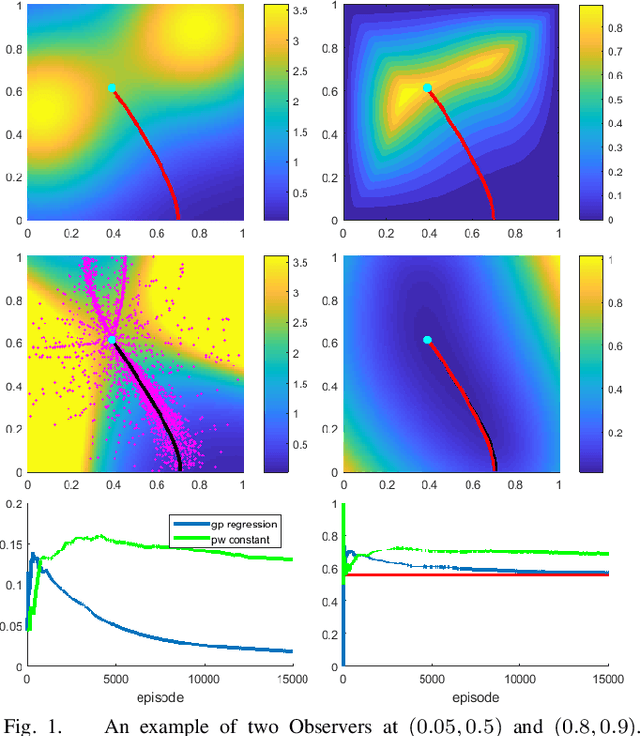
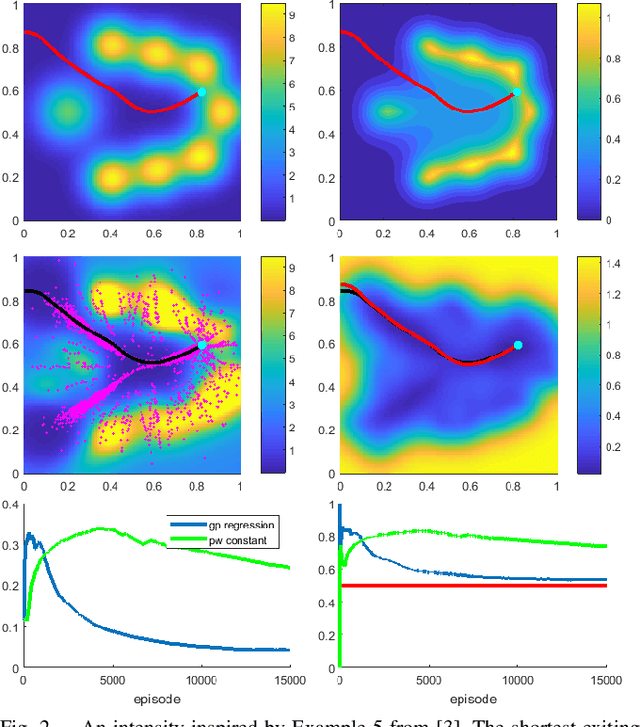
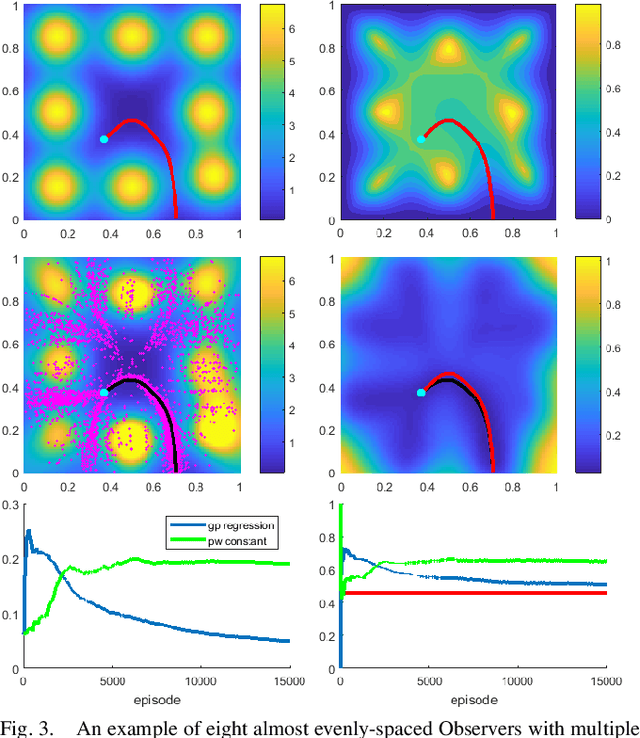
We consider a 2D continuous path planning problem with a completely unknown intensity of random termination: an Evader is trying to escape a domain while minimizing the cumulative risk of detection (termination) by adversarial Observers. Those Observers' surveillance intensity is a priori unknown and has to be learned through repetitive path planning. We propose a new algorithm that utilizes Gaussian process regression to model the unknown surveillance intensity and relies on a confidence bound technique to promote strategic exploration. We illustrate our method through several examples and confirm the convergence of averaged regret experimentally.

Scaling Gaussian Processes with Derivative Information Using Variational Inference

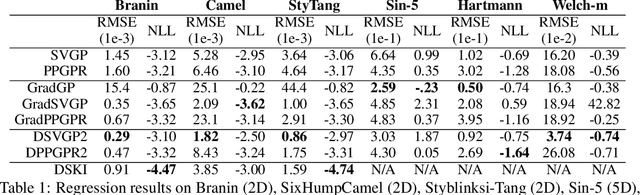
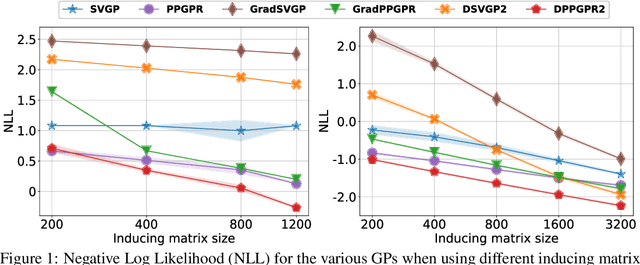
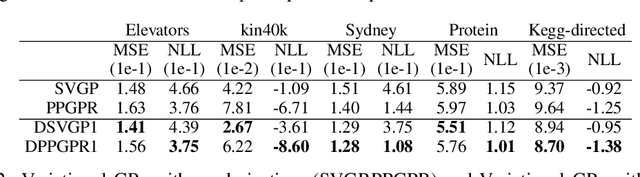
Gaussian processes with derivative information are useful in many settings where derivative information is available, including numerous Bayesian optimization and regression tasks that arise in the natural sciences. Incorporating derivative observations, however, comes with a dominating $O(N^3D^3)$ computational cost when training on $N$ points in $D$ input dimensions. This is intractable for even moderately sized problems. While recent work has addressed this intractability in the low-$D$ setting, the high-$N$, high-$D$ setting is still unexplored and of great value, particularly as machine learning problems increasingly become high dimensional. In this paper, we introduce methods to achieve fully scalable Gaussian process regression with derivatives using variational inference. Analogous to the use of inducing values to sparsify the labels of a training set, we introduce the concept of inducing directional derivatives to sparsify the partial derivative information of a training set. This enables us to construct a variational posterior that incorporates derivative information but whose size depends neither on the full dataset size $N$ nor the full dimensionality $D$. We demonstrate the full scalability of our approach on a variety of tasks, ranging from a high dimensional stellarator fusion regression task to training graph convolutional neural networks on Pubmed using Bayesian optimization. Surprisingly, we find that our approach can improve regression performance even in settings where only label data is available.

Density of States Graph Kernels

An important problem on graph-structured data is that of quantifying similarity between graphs. Graph kernels are an established technique for such tasks; in particular, those based on random walks and return probabilities have proven to be effective in wide-ranging applications, from bioinformatics to social networks to computer vision. However, random walk kernels generally suffer from slowness and tottering, an effect which causes walks to overemphasize local graph topology, undercutting the importance of global structure. To correct for these issues, we recast return probability graph kernels under the more general framework of density of states -- a framework which uses the lens of spectral analysis to uncover graph motifs and properties hidden within the interior of the spectrum -- and use our interpretation to construct scalable, composite density of states based graph kernels which balance local and global information, leading to higher classification accuracies on a host of benchmark datasets.

On the Distribution of Minima in Intrinsic-Metric Rotation Averaging

Rotation Averaging is a non-convex optimization problem that determines orientations of a collection of cameras from their images of a 3D scene. The problem has been studied using a variety of distances and robustifiers. The intrinsic (or geodesic) distance on SO(3) is geometrically meaningful; but while some extrinsic distance-based solvers admit (conditional) guarantees of correctness, no comparable results have been found under the intrinsic metric. In this paper, we study the spatial distribution of local minima. First, we do a novel empirical study to demonstrate sharp transitions in qualitative behavior: as problems become noisier, they transition from a single (easy-to-find) dominant minimum to a cost surface filled with minima. In the second part of this paper we derive a theoretical bound for when this transition occurs. This is an extension of the results of [24], which used local convexity as a proxy to study the difficulty of problem. By recognizing the underlying quotient manifold geometry of the problem we achieve an n-fold improvement over prior work. Incidentally, our analysis also extends the prior $l_2$ work to general $l_p$ costs. Our results suggest using algebraic connectivity as an indicator of problem difficulty.

Efficient Rollout Strategies for Bayesian Optimization

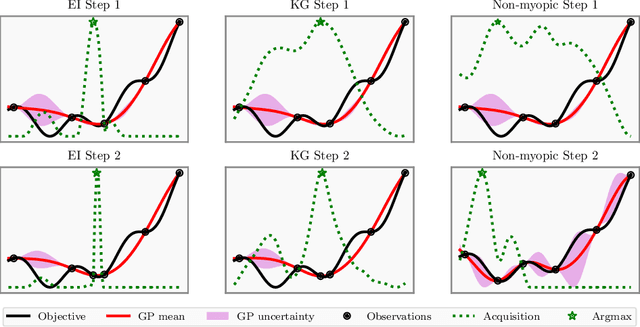
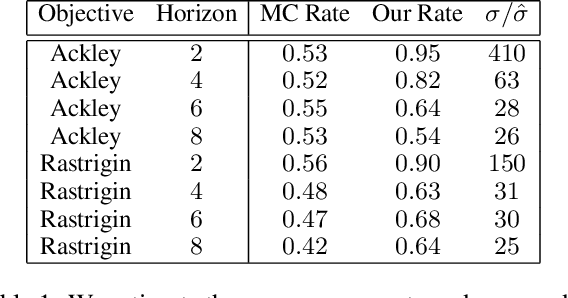
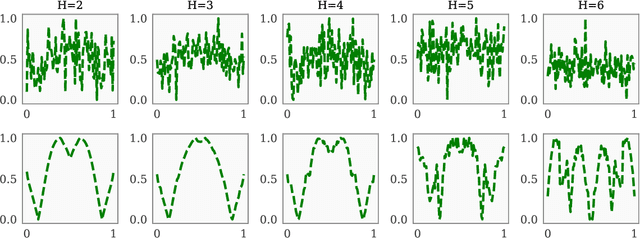
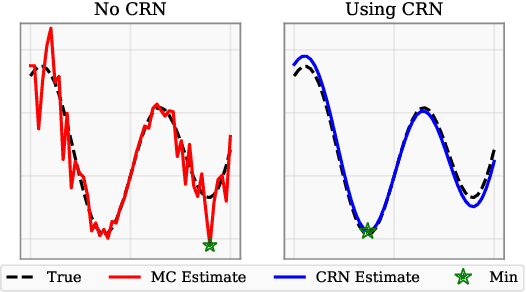
Bayesian optimization (BO) is a class of sample-efficient global optimization methods, where a probabilistic model conditioned on previous observations is used to determine future evaluations via the optimization of an acquisition function. Most acquisition functions are myopic, meaning that they only consider the impact of the next function evaluation. Non-myopic acquisition functions consider the impact of the next $h$ function evaluations and are typically computed through rollout, in which $h$ steps of BO are simulated. These rollout acquisition functions are defined as $h$-dimensional integrals, and are expensive to compute and optimize. We show that a combination of quasi-Monte Carlo, common random numbers, and control variates significantly reduce the computational burden of rollout. We then formulate a policy-search based approach that removes the need to optimize the rollout acquisition function. Finally, we discuss the qualitative behavior of rollout policies in the setting of multi-modal objectives and model error.

pySOT and POAP: An event-driven asynchronous framework for surrogate optimization

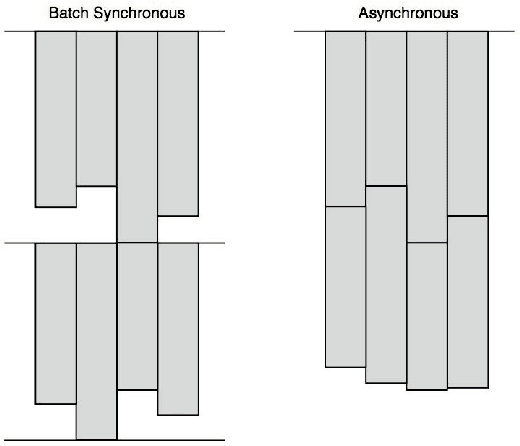
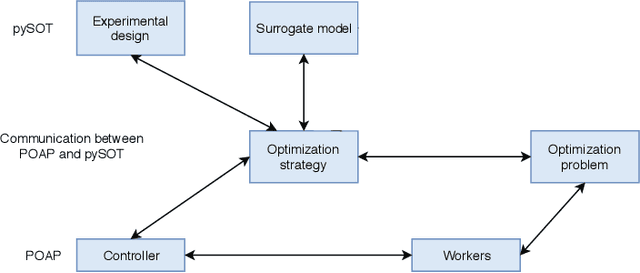
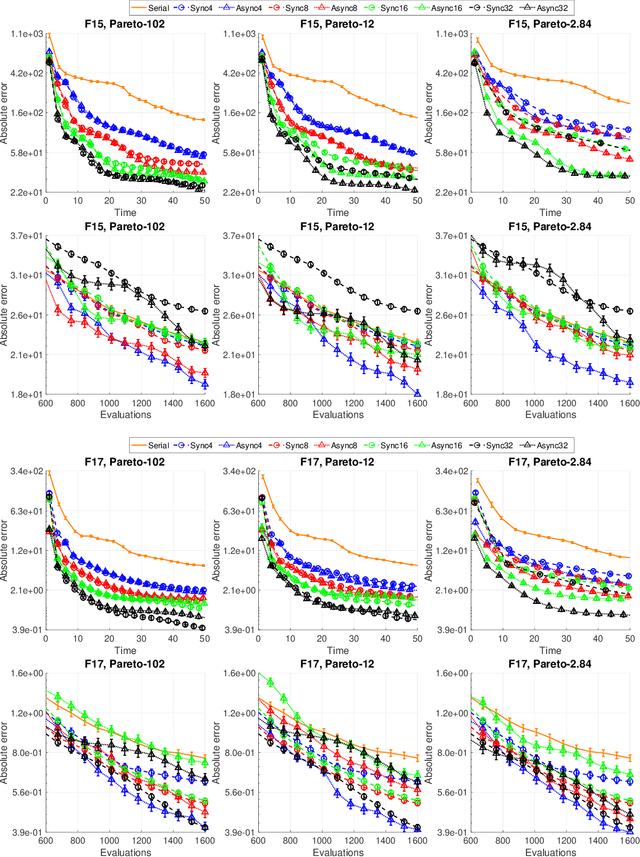
This paper describes Plumbing for Optimization with Asynchronous Parallelism (POAP) and the Python Surrogate Optimization Toolbox (pySOT). POAP is an event-driven framework for building and combining asynchronous optimization strategies, designed for global optimization of expensive functions where concurrent function evaluations are useful. POAP consists of three components: a worker pool capable of function evaluations, strategies to propose evaluations or other actions, and a controller that mediates the interaction between the workers and strategies. pySOT is a collection of synchronous and asynchronous surrogate optimization strategies, implemented in the POAP framework. We support the stochastic RBF method by Regis and Shoemaker along with various extensions of this method, and a general surrogate optimization strategy that covers most Bayesian optimization methods. We have implemented many different surrogate models, experimental designs, acquisition functions, and a large set of test problems. We make an extensive comparison between synchronous and asynchronous parallelism and find that the advantage of asynchronous computation increases as the variance of the evaluation time or number of processors increases. We observe a close to linear speed-up with 4, 8, and 16 processors in both the synchronous and asynchronous setting.

Scaling Gaussian Process Regression with Derivatives

Gaussian processes (GPs) with derivatives are useful in many applications, including Bayesian optimization, implicit surface reconstruction, and terrain reconstruction. Fitting a GP to function values and derivatives at $n$ points in $d$ dimensions requires linear solves and log determinants with an ${n(d+1) \times n(d+1)}$ positive definite matrix -- leading to prohibitive $\mathcal{O}(n^3d^3)$ computations for standard direct methods. We propose iterative solvers using fast $\mathcal{O}(nd)$ matrix-vector multiplications (MVMs), together with pivoted Cholesky preconditioning that cuts the iterations to convergence by several orders of magnitude, allowing for fast kernel learning and prediction. Our approaches, together with dimensionality reduction, enables Bayesian optimization with derivatives to scale to high-dimensional problems and large evaluation budgets.

GPyTorch: Blackbox Matrix-Matrix Gaussian Process Inference with GPU Acceleration

Despite advances in scalable models, the inference tools used for Gaussian processes (GPs) have yet to fully capitalize on developments in computing hardware. We present an efficient and general approach to GP inference based on Blackbox Matrix-Matrix multiplication (BBMM). BBMM inference uses a modified batched version of the conjugate gradients algorithm to derive all terms for training and inference in a single call. BBMM reduces the asymptotic complexity of exact GP inference from $O(n^3)$ to $O(n^2)$. Adapting this algorithm to scalable approximations and complex GP models simply requires a routine for efficient matrix-matrix multiplication with the kernel and its derivative. In addition, BBMM uses a specialized preconditioner to substantially speed up convergence. In experiments we show that BBMM effectively uses GPU hardware to dramatically accelerate both exact GP inference and scalable approximations. Additionally, we provide GPyTorch, a software platform for scalable GP inference via BBMM, built on PyTorch.