SigOpt Mulch: An Intelligent System for AutoML of Gradient Boosted Trees

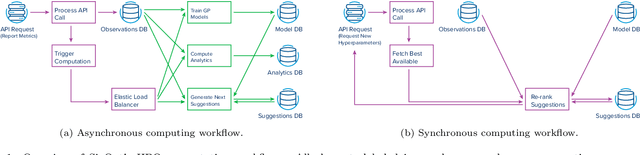
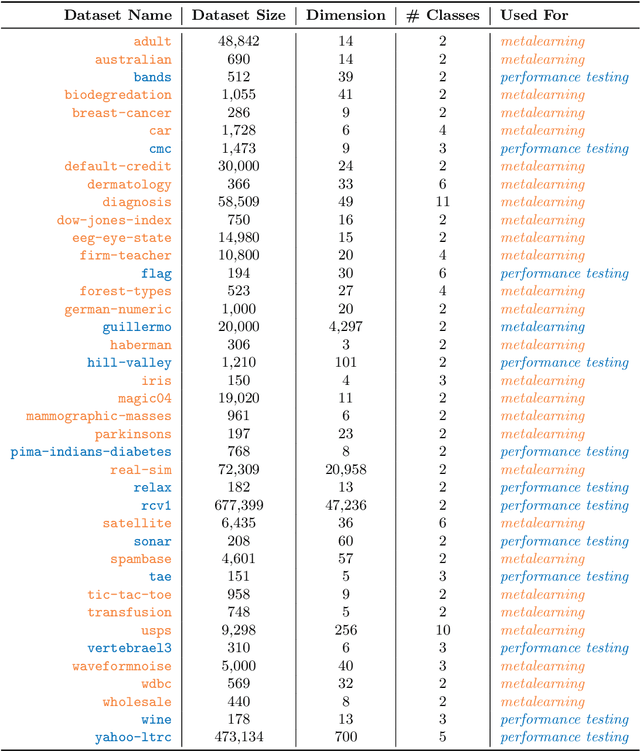
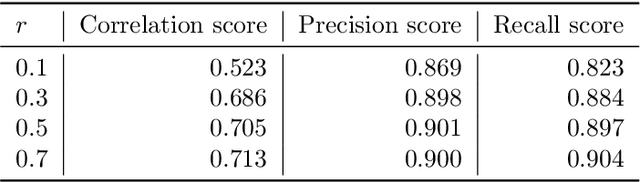
Gradient boosted trees (GBTs) are ubiquitous models used by researchers, machine learning (ML) practitioners, and data scientists because of their robust performance, interpretable behavior, and ease-of-use. One critical challenge in training GBTs is the tuning of their hyperparameters. In practice, selecting these hyperparameters is often done manually. Recently, the ML community has advocated for tuning hyperparameters through black-box optimization and developed state-of-the-art systems to do so. However, applying such systems to tune GBTs suffers from two drawbacks. First, these systems are not \textit{model-aware}, rather they are designed to apply to a \textit{generic} model; this leaves significant optimization performance on the table. Second, using these systems requires \textit{domain knowledge} such as the choice of hyperparameter search space, which is an antithesis to the automatic experimentation that black-box optimization aims to provide. In this paper, we present SigOpt Mulch, a model-aware hyperparameter tuning system specifically designed for automated tuning of GBTs that provides two improvements over existing systems. First, Mulch leverages powerful techniques in metalearning and multifidelity optimization to perform model-aware hyperparameter optimization. Second, it automates the process of learning performant hyperparameters by making intelligent decisions about the optimization search space, thus reducing the need for user domain knowledge. These innovations allow Mulch to identify good GBT hyperparameters far more efficiently -- and in a more seamless and user-friendly way -- than existing black-box hyperparameter tuning systems.

Scaling Gaussian Processes with Derivative Information Using Variational Inference

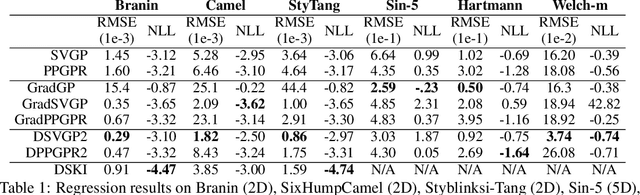
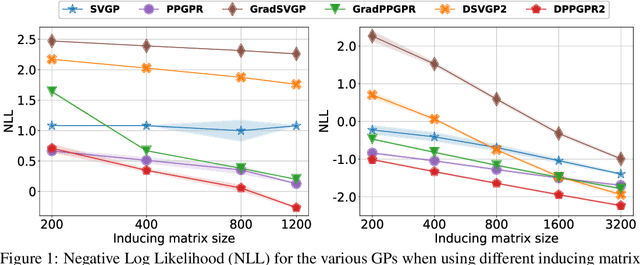
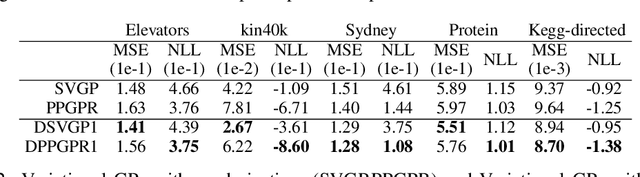
Gaussian processes with derivative information are useful in many settings where derivative information is available, including numerous Bayesian optimization and regression tasks that arise in the natural sciences. Incorporating derivative observations, however, comes with a dominating $O(N^3D^3)$ computational cost when training on $N$ points in $D$ input dimensions. This is intractable for even moderately sized problems. While recent work has addressed this intractability in the low-$D$ setting, the high-$N$, high-$D$ setting is still unexplored and of great value, particularly as machine learning problems increasingly become high dimensional. In this paper, we introduce methods to achieve fully scalable Gaussian process regression with derivatives using variational inference. Analogous to the use of inducing values to sparsify the labels of a training set, we introduce the concept of inducing directional derivatives to sparsify the partial derivative information of a training set. This enables us to construct a variational posterior that incorporates derivative information but whose size depends neither on the full dataset size $N$ nor the full dimensionality $D$. We demonstrate the full scalability of our approach on a variety of tasks, ranging from a high dimensional stellarator fusion regression task to training graph convolutional neural networks on Pubmed using Bayesian optimization. Surprisingly, we find that our approach can improve regression performance even in settings where only label data is available.