SigOpt Mulch: An Intelligent System for AutoML of Gradient Boosted Trees

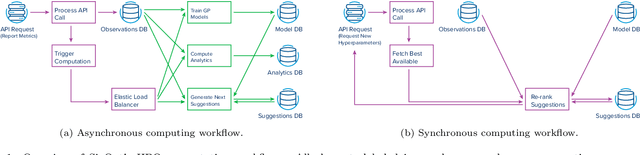
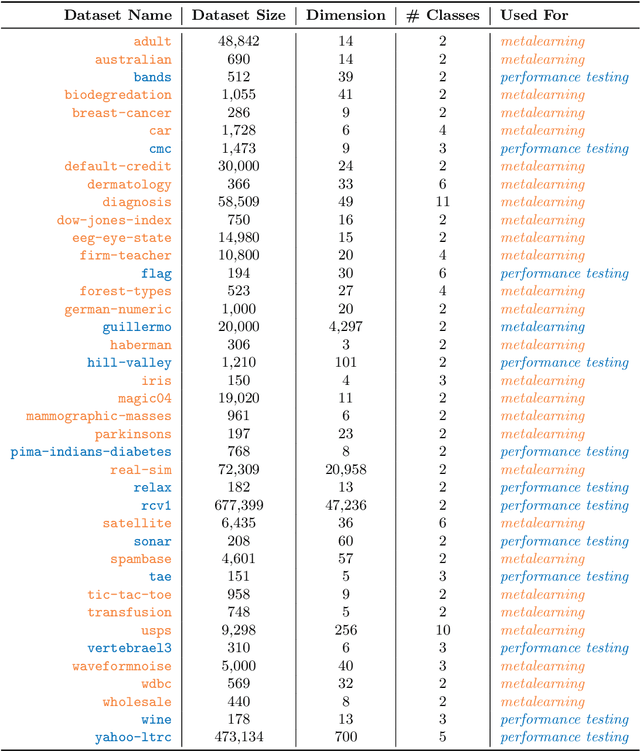
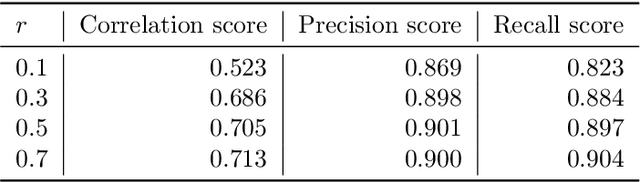
Gradient boosted trees (GBTs) are ubiquitous models used by researchers, machine learning (ML) practitioners, and data scientists because of their robust performance, interpretable behavior, and ease-of-use. One critical challenge in training GBTs is the tuning of their hyperparameters. In practice, selecting these hyperparameters is often done manually. Recently, the ML community has advocated for tuning hyperparameters through black-box optimization and developed state-of-the-art systems to do so. However, applying such systems to tune GBTs suffers from two drawbacks. First, these systems are not \textit{model-aware}, rather they are designed to apply to a \textit{generic} model; this leaves significant optimization performance on the table. Second, using these systems requires \textit{domain knowledge} such as the choice of hyperparameter search space, which is an antithesis to the automatic experimentation that black-box optimization aims to provide. In this paper, we present SigOpt Mulch, a model-aware hyperparameter tuning system specifically designed for automated tuning of GBTs that provides two improvements over existing systems. First, Mulch leverages powerful techniques in metalearning and multifidelity optimization to perform model-aware hyperparameter optimization. Second, it automates the process of learning performant hyperparameters by making intelligent decisions about the optimization search space, thus reducing the need for user domain knowledge. These innovations allow Mulch to identify good GBT hyperparameters far more efficiently -- and in a more seamless and user-friendly way -- than existing black-box hyperparameter tuning systems.

Achieving Diversity in Objective Space for Sample-efficient Search of Multiobjective Optimization Problems

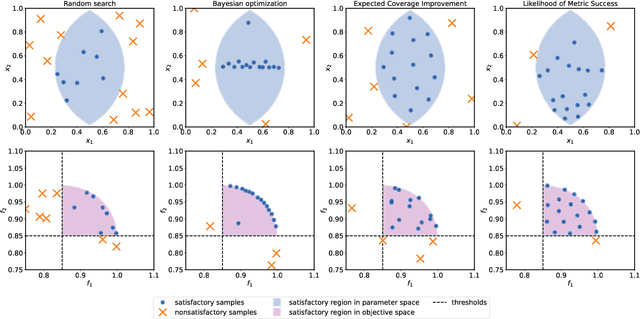
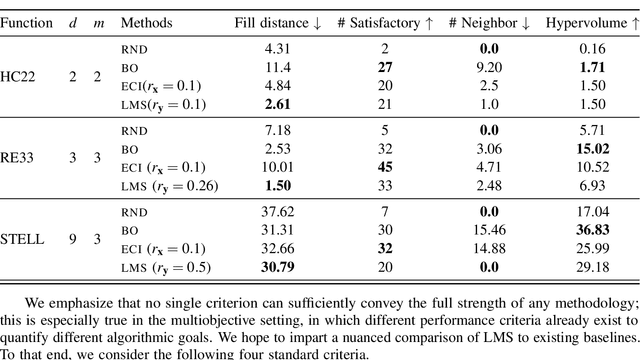
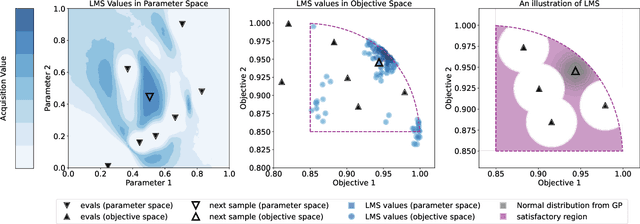
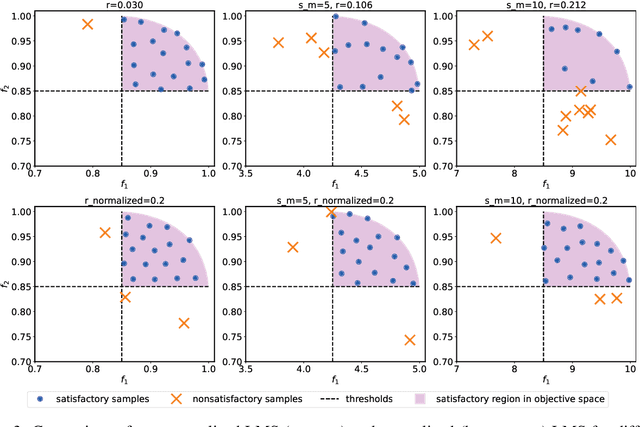
Efficiently solving multi-objective optimization problems for simulation optimization of important scientific and engineering applications such as materials design is becoming an increasingly important research topic. This is due largely to the expensive costs associated with said applications, and the resulting need for sample-efficient, multiobjective optimization methods that efficiently explore the Pareto frontier to expose a promising set of design solutions. We propose moving away from using explicit optimization to identify the Pareto frontier and instead suggest searching for a diverse set of outcomes that satisfy user-specified performance criteria. This method presents decision makers with a robust pool of promising design decisions and helps them better understand the space of good solutions. To achieve this outcome, we introduce the Likelihood of Metric Satisfaction (LMS) acquisition function, analyze its behavior and properties, and demonstrate its viability on various problems.

Efficient Rollout Strategies for Bayesian Optimization

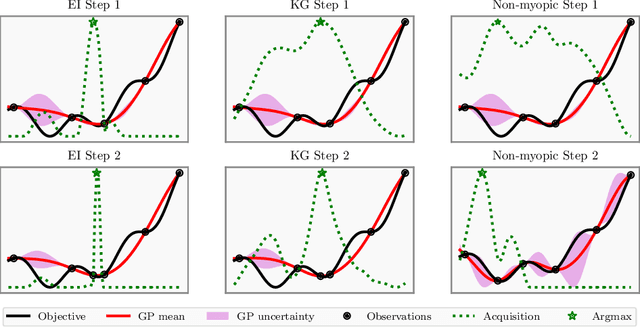
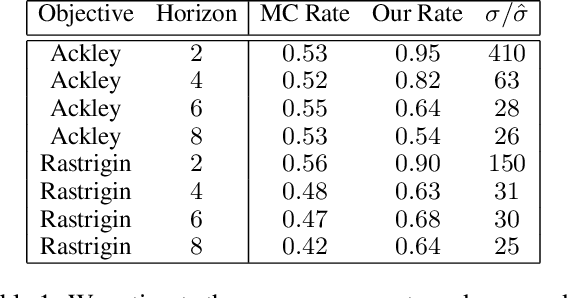
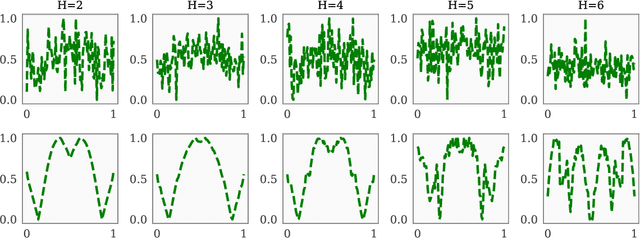
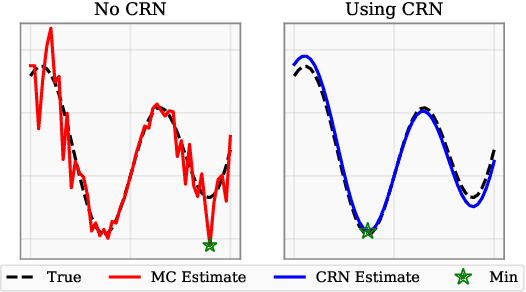
Bayesian optimization (BO) is a class of sample-efficient global optimization methods, where a probabilistic model conditioned on previous observations is used to determine future evaluations via the optimization of an acquisition function. Most acquisition functions are myopic, meaning that they only consider the impact of the next function evaluation. Non-myopic acquisition functions consider the impact of the next $h$ function evaluations and are typically computed through rollout, in which $h$ steps of BO are simulated. These rollout acquisition functions are defined as $h$-dimensional integrals, and are expensive to compute and optimize. We show that a combination of quasi-Monte Carlo, common random numbers, and control variates significantly reduce the computational burden of rollout. We then formulate a policy-search based approach that removes the need to optimize the rollout acquisition function. Finally, we discuss the qualitative behavior of rollout policies in the setting of multi-modal objectives and model error.