SigOpt Mulch: An Intelligent System for AutoML of Gradient Boosted Trees

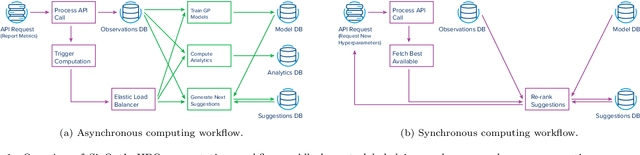
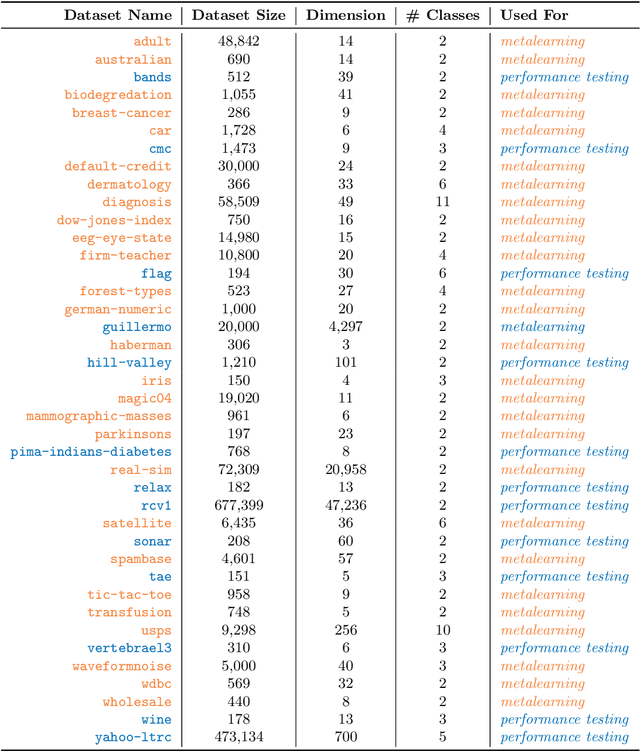
Gradient boosted trees (GBTs) are ubiquitous models used by researchers, machine learning (ML) practitioners, and data scientists because of their robust performance, interpretable behavior, and ease-of-use. One critical challenge in training GBTs is the tuning of their hyperparameters. In practice, selecting these hyperparameters is often done manually. Recently, the ML community has advocated for tuning hyperparameters through black-box optimization and developed state-of-the-art systems to do so. However, applying such systems to tune GBTs suffers from two drawbacks. First, these systems are not \textit{model-aware}, rather they are designed to apply to a \textit{generic} model; this leaves significant optimization performance on the table. Second, using these systems requires \textit{domain knowledge} such as the choice of hyperparameter search space, which is an antithesis to the automatic experimentation that black-box optimization aims to provide. In this paper, we present SigOpt Mulch, a model-aware hyperparameter tuning system specifically designed for automated tuning of GBTs that provides two improvements over existing systems. First, Mulch leverages powerful techniques in metalearning and multifidelity optimization to perform model-aware hyperparameter optimization. Second, it automates the process of learning performant hyperparameters by making intelligent decisions about the optimization search space, thus reducing the need for user domain knowledge. These innovations allow Mulch to identify good GBT hyperparameters far more efficiently -- and in a more seamless and user-friendly way -- than existing black-box hyperparameter tuning systems.

Achieving Diversity in Objective Space for Sample-efficient Search of Multiobjective Optimization Problems

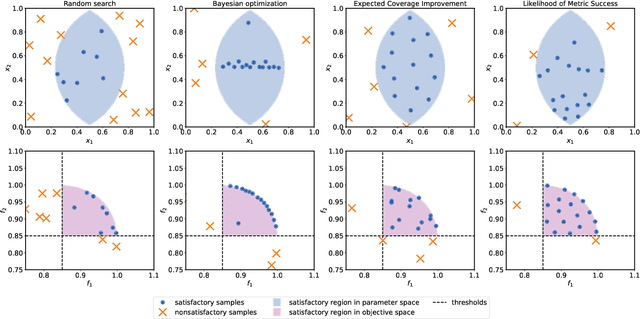
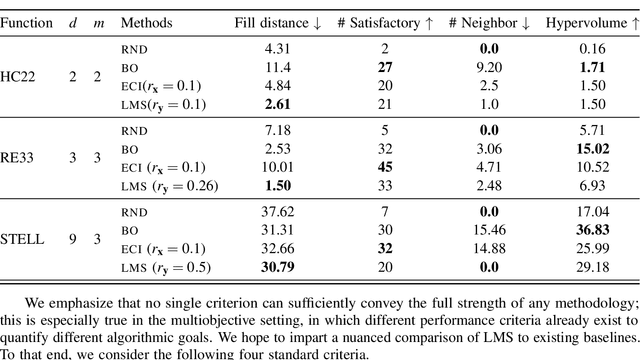
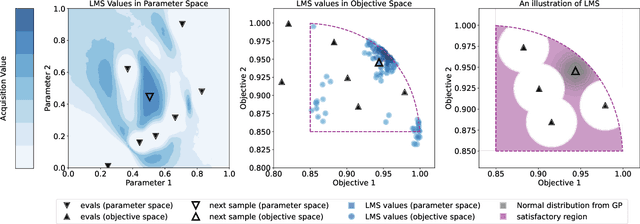
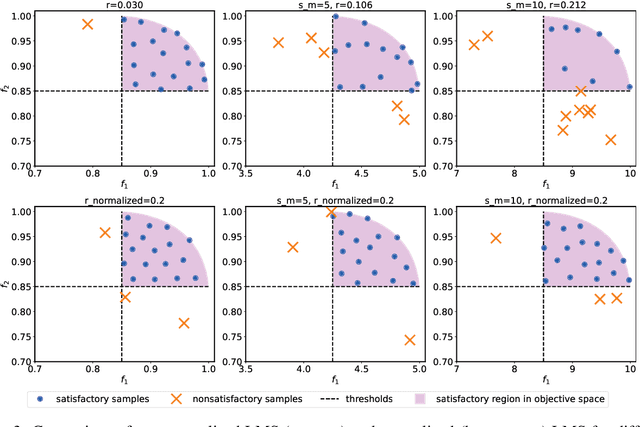
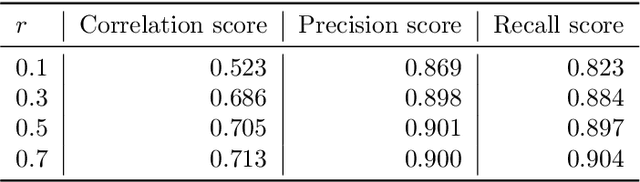
Efficiently solving multi-objective optimization problems for simulation optimization of important scientific and engineering applications such as materials design is becoming an increasingly important research topic. This is due largely to the expensive costs associated with said applications, and the resulting need for sample-efficient, multiobjective optimization methods that efficiently explore the Pareto frontier to expose a promising set of design solutions. We propose moving away from using explicit optimization to identify the Pareto frontier and instead suggest searching for a diverse set of outcomes that satisfy user-specified performance criteria. This method presents decision makers with a robust pool of promising design decisions and helps them better understand the space of good solutions. To achieve this outcome, we introduce the Likelihood of Metric Satisfaction (LMS) acquisition function, analyze its behavior and properties, and demonstrate its viability on various problems.

A Nonmyopic Approach to Cost-Constrained Bayesian Optimization

Bayesian optimization (BO) is a popular method for optimizing expensive-to-evaluate black-box functions. BO budgets are typically given in iterations, which implicitly assumes each evaluation has the same cost. In fact, in many BO applications, evaluation costs vary significantly in different regions of the search space. In hyperparameter optimization, the time spent on neural network training increases with layer size; in clinical trials, the monetary cost of drug compounds vary; and in optimal control, control actions have differing complexities. Cost-constrained BO measures convergence with alternative cost metrics such as time, money, or energy, for which the sample efficiency of standard BO methods is ill-suited. For cost-constrained BO, cost efficiency is far more important than sample efficiency. In this paper, we formulate cost-constrained BO as a constrained Markov decision process (CMDP), and develop an efficient rollout approximation to the optimal CMDP policy that takes both the cost and future iterations into account. We validate our method on a collection of hyperparameter optimization problems as well as a sensor set selection application.

Cost-aware Bayesian Optimization

Bayesian optimization (BO) is a class of global optimization algorithms, suitable for minimizing an expensive objective function in as few function evaluations as possible. While BO budgets are typically given in iterations, this implicitly measures convergence in terms of iteration count and assumes each evaluation has identical cost. In practice, evaluation costs may vary in different regions of the search space. For example, the cost of neural network training increases quadratically with layer size, which is a typical hyperparameter. Cost-aware BO measures convergence with alternative cost metrics such as time, energy, or money, for which vanilla BO methods are unsuited. We introduce Cost Apportioned BO (CArBO), which attempts to minimize an objective function in as little cost as possible. CArBO combines a cost-effective initial design with a cost-cooled optimization phase which depreciates a learned cost model as iterations proceed. On a set of 20 black-box function optimization problems we show that, given the same cost budget, CArBO finds significantly better hyperparameter configurations than competing methods.

Efficient Rollout Strategies for Bayesian Optimization

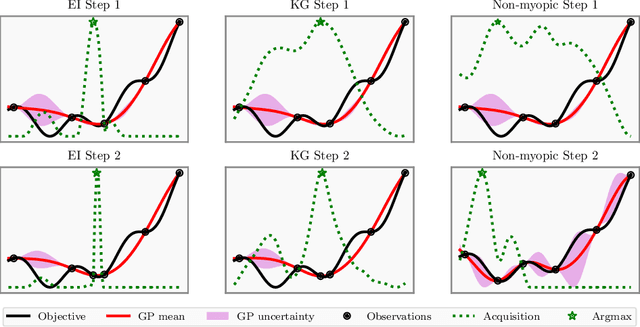
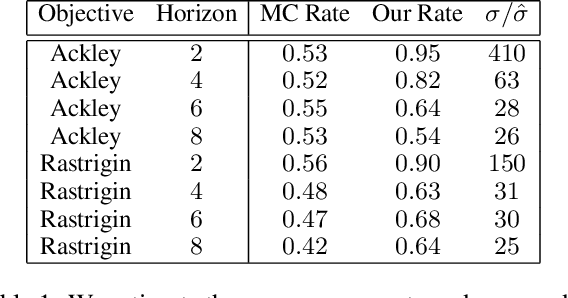
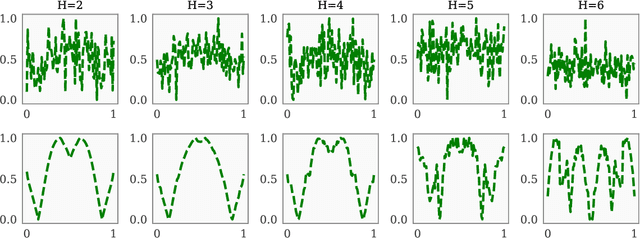
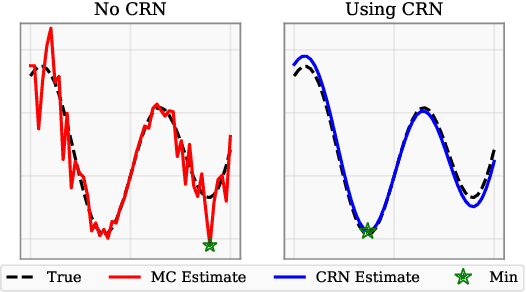
Bayesian optimization (BO) is a class of sample-efficient global optimization methods, where a probabilistic model conditioned on previous observations is used to determine future evaluations via the optimization of an acquisition function. Most acquisition functions are myopic, meaning that they only consider the impact of the next function evaluation. Non-myopic acquisition functions consider the impact of the next $h$ function evaluations and are typically computed through rollout, in which $h$ steps of BO are simulated. These rollout acquisition functions are defined as $h$-dimensional integrals, and are expensive to compute and optimize. We show that a combination of quasi-Monte Carlo, common random numbers, and control variates significantly reduce the computational burden of rollout. We then formulate a policy-search based approach that removes the need to optimize the rollout acquisition function. Finally, we discuss the qualitative behavior of rollout policies in the setting of multi-modal objectives and model error.

Scaling Gaussian Process Regression with Derivatives

Gaussian processes (GPs) with derivatives are useful in many applications, including Bayesian optimization, implicit surface reconstruction, and terrain reconstruction. Fitting a GP to function values and derivatives at $n$ points in $d$ dimensions requires linear solves and log determinants with an ${n(d+1) \times n(d+1)}$ positive definite matrix -- leading to prohibitive $\mathcal{O}(n^3d^3)$ computations for standard direct methods. We propose iterative solvers using fast $\mathcal{O}(nd)$ matrix-vector multiplications (MVMs), together with pivoted Cholesky preconditioning that cuts the iterations to convergence by several orders of magnitude, allowing for fast kernel learning and prediction. Our approaches, together with dimensionality reduction, enables Bayesian optimization with derivatives to scale to high-dimensional problems and large evaluation budgets.