Achieving Diversity in Objective Space for Sample-efficient Search of Multiobjective Optimization Problems
Paper and Code
Jun 23, 2023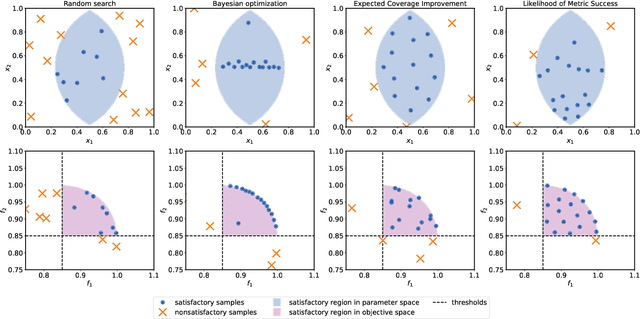
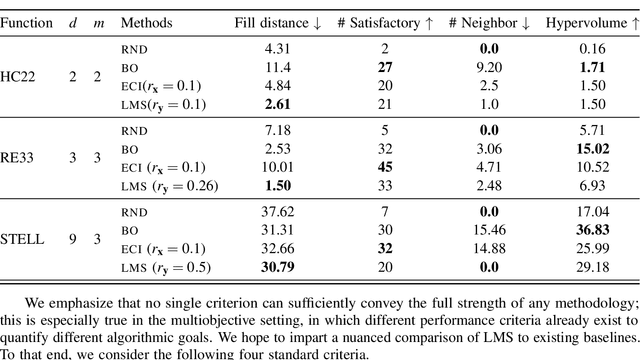
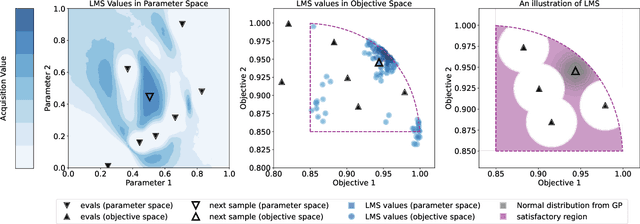
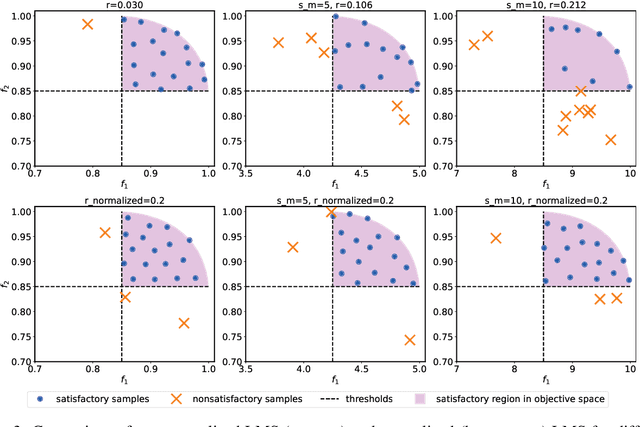
Efficiently solving multi-objective optimization problems for simulation optimization of important scientific and engineering applications such as materials design is becoming an increasingly important research topic. This is due largely to the expensive costs associated with said applications, and the resulting need for sample-efficient, multiobjective optimization methods that efficiently explore the Pareto frontier to expose a promising set of design solutions. We propose moving away from using explicit optimization to identify the Pareto frontier and instead suggest searching for a diverse set of outcomes that satisfy user-specified performance criteria. This method presents decision makers with a robust pool of promising design decisions and helps them better understand the space of good solutions. To achieve this outcome, we introduce the Likelihood of Metric Satisfaction (LMS) acquisition function, analyze its behavior and properties, and demonstrate its viability on various problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge