Surveillance Evasion Through Bayesian Reinforcement Learning

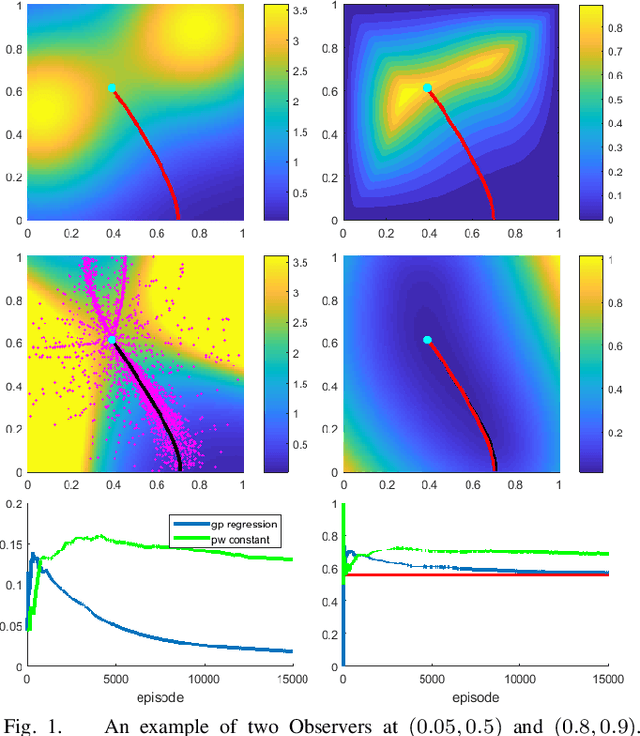
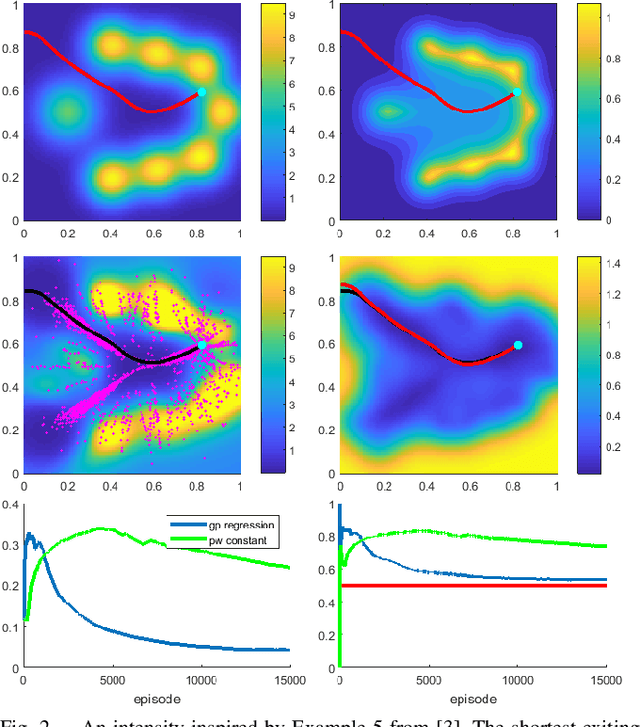
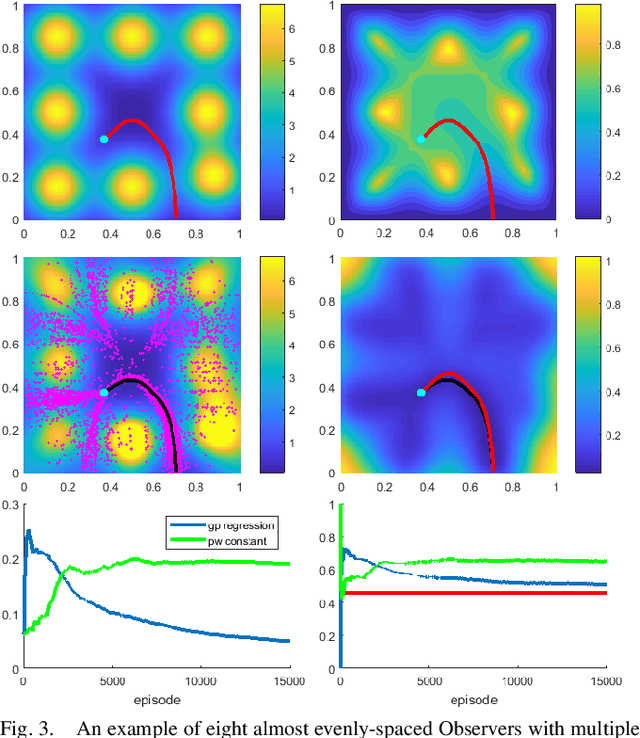
We consider a 2D continuous path planning problem with a completely unknown intensity of random termination: an Evader is trying to escape a domain while minimizing the cumulative risk of detection (termination) by adversarial Observers. Those Observers' surveillance intensity is a priori unknown and has to be learned through repetitive path planning. We propose a new algorithm that utilizes Gaussian process regression to model the unknown surveillance intensity and relies on a confidence bound technique to promote strategic exploration. We illustrate our method through several examples and confirm the convergence of averaged regret experimentally.

Spline parameterization of neural network controls for deep learning

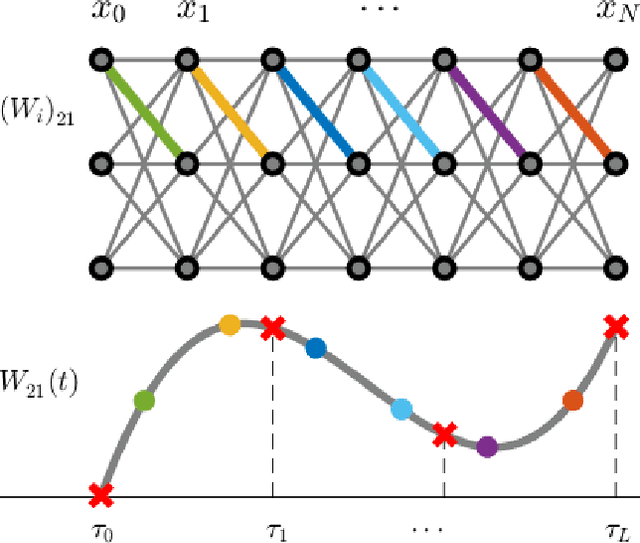
Based on the continuous interpretation of deep learning cast as an optimal control problem, this paper investigates the benefits of employing B-spline basis functions to parameterize neural network controls across the layers. Rather than equipping each layer of a discretized ODE-network with a set of trainable weights, we choose a fixed number of B-spline basis functions whose coefficients are the trainable parameters of the neural network. Decoupling the trainable parameters from the layers of the neural network enables us to investigate and adapt the accuracy of the network propagation separated from the optimization learning problem. We numerically show that the spline-based neural network increases robustness of the learning problem towards hyperparameters due to increased stability and accuracy of the network propagation. Further, training on B-spline coefficients rather than layer weights directly enables a reduction in the number of trainable parameters.