Surveillance Evasion Through Bayesian Reinforcement Learning

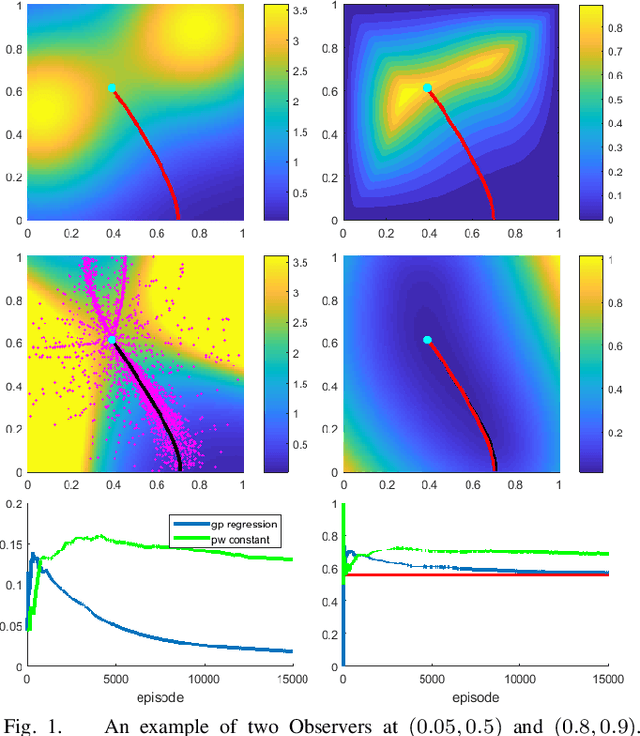
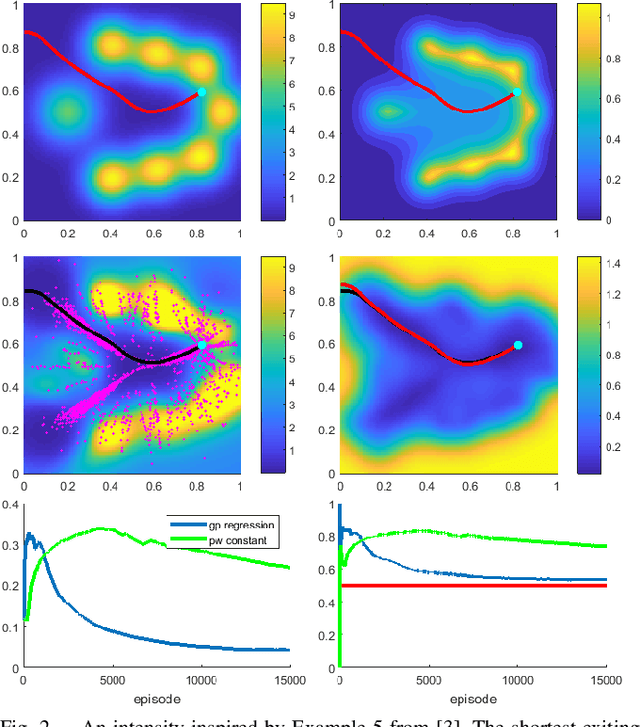
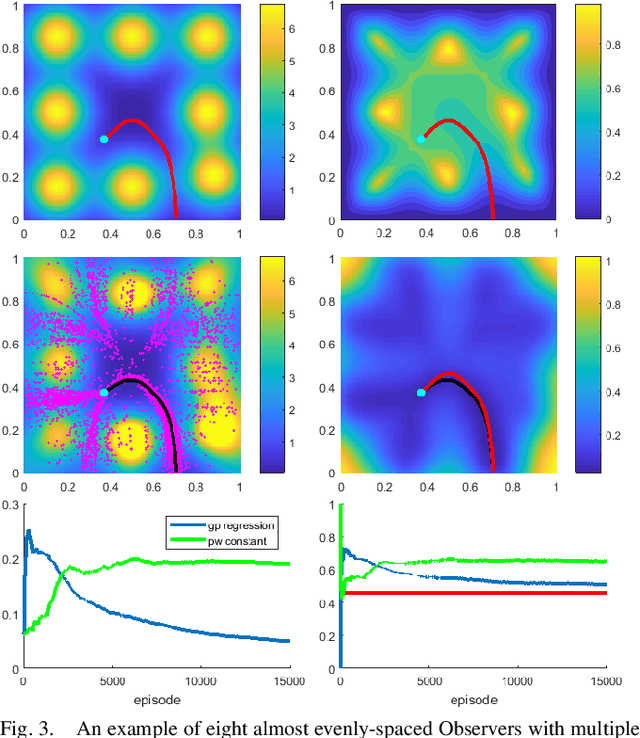
We consider a 2D continuous path planning problem with a completely unknown intensity of random termination: an Evader is trying to escape a domain while minimizing the cumulative risk of detection (termination) by adversarial Observers. Those Observers' surveillance intensity is a priori unknown and has to be learned through repetitive path planning. We propose a new algorithm that utilizes Gaussian process regression to model the unknown surveillance intensity and relies on a confidence bound technique to promote strategic exploration. We illustrate our method through several examples and confirm the convergence of averaged regret experimentally.