Stefanie Günther
Spline parameterization of neural network controls for deep learning
Feb 27, 2021

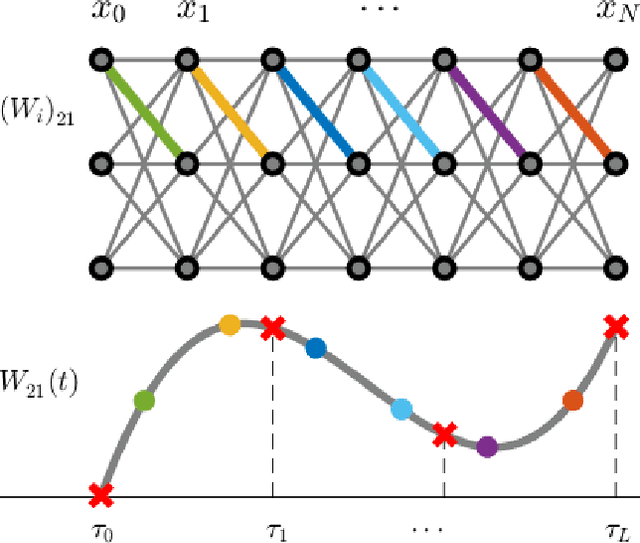

Abstract:Based on the continuous interpretation of deep learning cast as an optimal control problem, this paper investigates the benefits of employing B-spline basis functions to parameterize neural network controls across the layers. Rather than equipping each layer of a discretized ODE-network with a set of trainable weights, we choose a fixed number of B-spline basis functions whose coefficients are the trainable parameters of the neural network. Decoupling the trainable parameters from the layers of the neural network enables us to investigate and adapt the accuracy of the network propagation separated from the optimization learning problem. We numerically show that the spline-based neural network increases robustness of the learning problem towards hyperparameters due to increased stability and accuracy of the network propagation. Further, training on B-spline coefficients rather than layer weights directly enables a reduction in the number of trainable parameters.
Multilevel Initialization for Layer-Parallel Deep Neural Network Training
Dec 19, 2019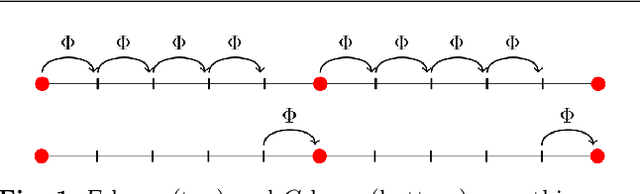
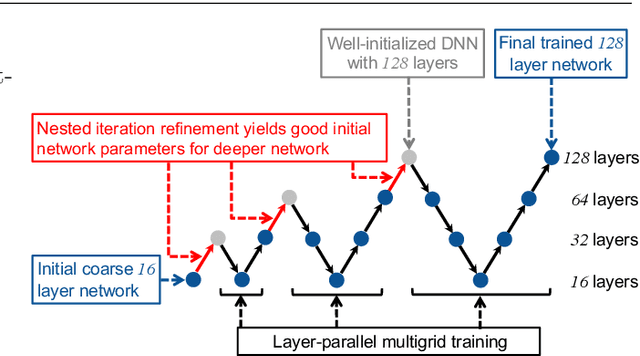
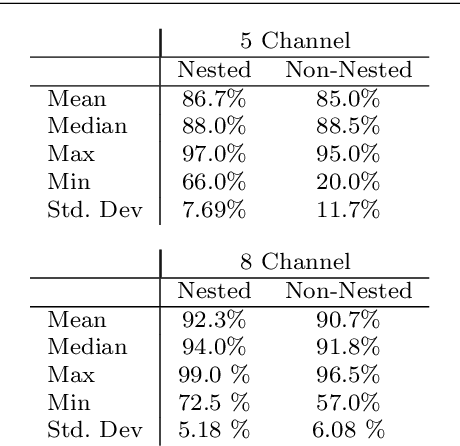

Abstract:This paper investigates multilevel initialization strategies for training very deep neural networks with a layer-parallel multigrid solver. The scheme is based on the continuous interpretation of the training problem as a problem of optimal control, in which neural networks are represented as discretizations of time-dependent ordinary differential equations. A key goal is to develop a method able to intelligently initialize the network parameters for the very deep networks enabled by scalable layer-parallel training. To do this, we apply a refinement strategy across the time domain, that is equivalent to refining in the layer dimension. The resulting refinements create deep networks, with good initializations for the network parameters coming from the coarser trained networks. We investigate the effectiveness of such multilevel "nested iteration" strategies for network training, showing supporting numerical evidence of reduced run time for equivalent accuracy. In addition, we study whether the initialization strategies provide a regularizing effect on the overall training process and reduce sensitivity to hyperparameters and randomness in initial network parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge