Multilevel Initialization for Layer-Parallel Deep Neural Network Training
Paper and Code
Dec 19, 2019
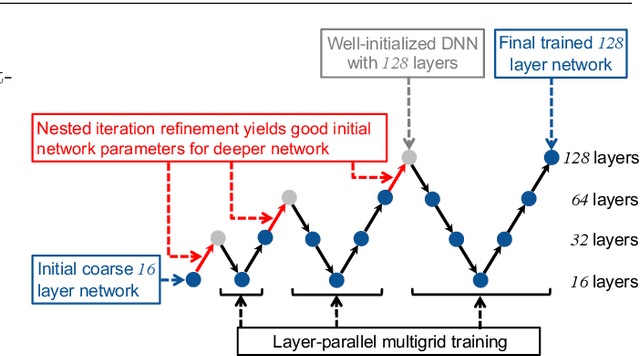
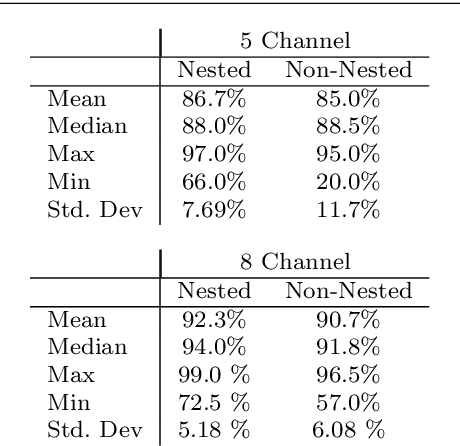
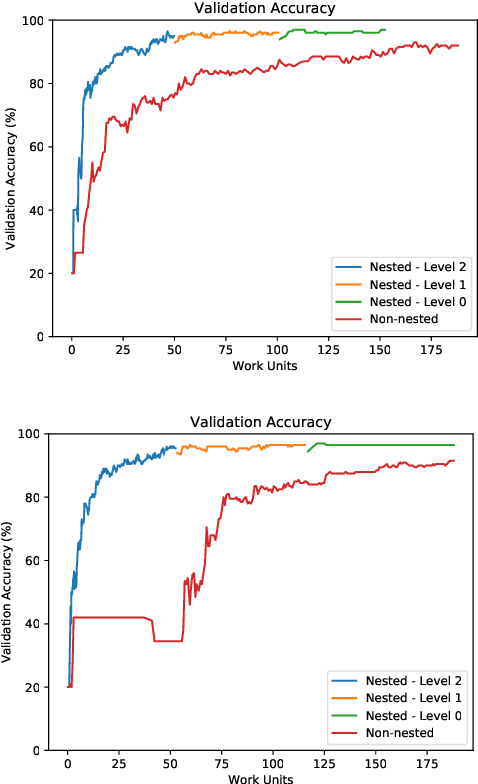
This paper investigates multilevel initialization strategies for training very deep neural networks with a layer-parallel multigrid solver. The scheme is based on the continuous interpretation of the training problem as a problem of optimal control, in which neural networks are represented as discretizations of time-dependent ordinary differential equations. A key goal is to develop a method able to intelligently initialize the network parameters for the very deep networks enabled by scalable layer-parallel training. To do this, we apply a refinement strategy across the time domain, that is equivalent to refining in the layer dimension. The resulting refinements create deep networks, with good initializations for the network parameters coming from the coarser trained networks. We investigate the effectiveness of such multilevel "nested iteration" strategies for network training, showing supporting numerical evidence of reduced run time for equivalent accuracy. In addition, we study whether the initialization strategies provide a regularizing effect on the overall training process and reduce sensitivity to hyperparameters and randomness in initial network parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge