Christine A. Shoemaker
pySOT and POAP: An event-driven asynchronous framework for surrogate optimization
Jul 30, 2019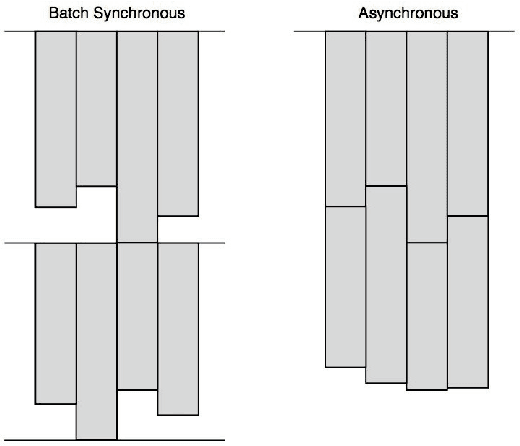

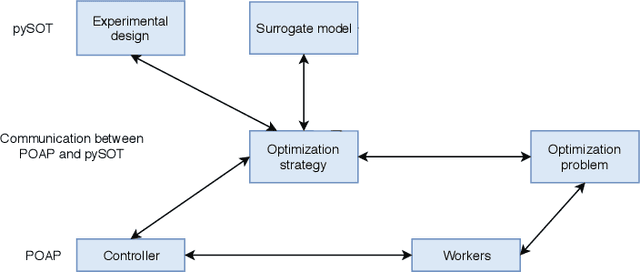
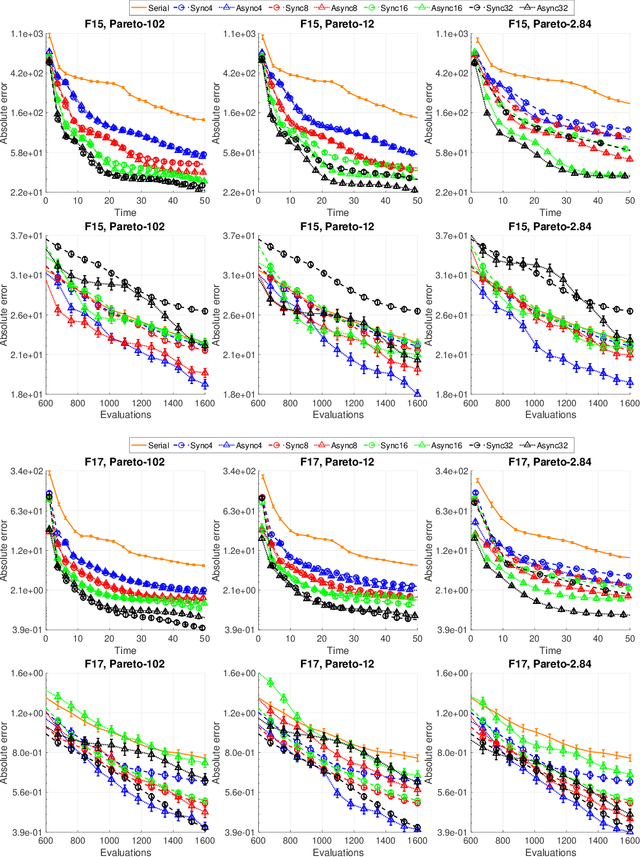
Abstract:This paper describes Plumbing for Optimization with Asynchronous Parallelism (POAP) and the Python Surrogate Optimization Toolbox (pySOT). POAP is an event-driven framework for building and combining asynchronous optimization strategies, designed for global optimization of expensive functions where concurrent function evaluations are useful. POAP consists of three components: a worker pool capable of function evaluations, strategies to propose evaluations or other actions, and a controller that mediates the interaction between the workers and strategies. pySOT is a collection of synchronous and asynchronous surrogate optimization strategies, implemented in the POAP framework. We support the stochastic RBF method by Regis and Shoemaker along with various extensions of this method, and a general surrogate optimization strategy that covers most Bayesian optimization methods. We have implemented many different surrogate models, experimental designs, acquisition functions, and a large set of test problems. We make an extensive comparison between synchronous and asynchronous parallelism and find that the advantage of asynchronous computation increases as the variance of the evaluation time or number of processors increases. We observe a close to linear speed-up with 4, 8, and 16 processors in both the synchronous and asynchronous setting.
Efficient Multi-Objective Optimization through Population-based Parallel Surrogate Search
Mar 06, 2019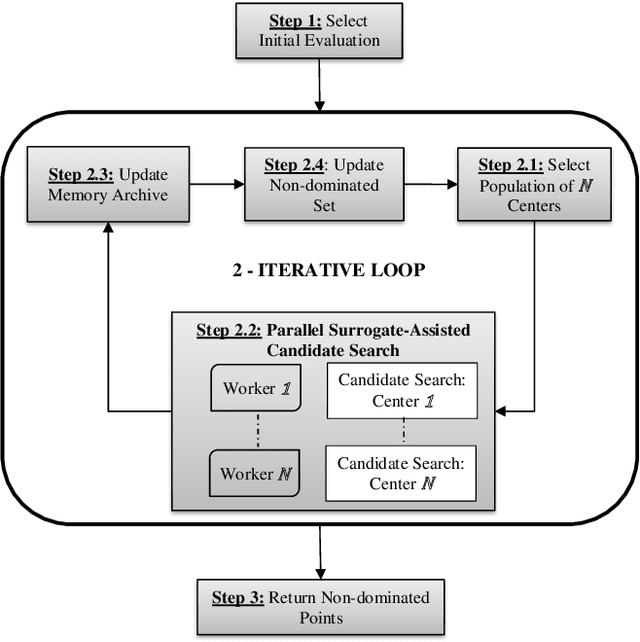
Abstract:Multi-Objective Optimization (MOO) is very difficult for expensive functions because most current MOO methods rely on a large number of function evaluations to get an accurate solution. We address this problem with surrogate approximation and parallel computation. We develop an MOO algorithm MOPLS-N for expensive functions that combines iteratively updated surrogate approximations of the objective functions with a structure for efficiently selecting a population of $N$ points so that the expensive objectives for all points are simultaneously evaluated on $N$ processors in each iteration. MOPLS incorporates Radial Basis Function (RBF) approximation, Tabu Search and local candidate search around multiple points to strike a balance between exploration, exploitation and diversification during each algorithm iteration. Eleven test problems (with 8 to 24 decision variables and two real-world watershed problems are used to compare performance of MOPLS to ParEGO, GOMORS, Borg, MOEA/D, and NSGA-III on a limited budget of evaluations with between 1 (serial) and 64 processors. MOPLS in serial is better than all non-RBF serial methods tested. Parallel speedup of MOPLS is higher than all other parallel algorithms with 16 and 64 processors. With both algorithms on 64 processors MOPLS is at least 2 times faster than NSGA-III on the watershed problems.
Sensitivity Analysis for Computationally Expensive Models using Optimization and Objective-oriented Surrogate Approximations
Feb 21, 2015

Abstract:In this paper, we focus on developing efficient sensitivity analysis methods for a computationally expensive objective function $f(x)$ in the case that the minimization of it has just been performed. Here "computationally expensive" means that each of its evaluation takes significant amount of time, and therefore our main goal to use a small number of function evaluations of $f(x)$ to further infer the sensitivity information of these different parameters. Correspondingly, we consider the optimization procedure as an adaptive experimental design and re-use its available function evaluations as the initial design points to establish a surrogate model $s(x)$ (or called response surface). The sensitivity analysis is performed on $s(x)$, which is an lieu of $f(x)$. Furthermore, we propose a new local multivariate sensitivity measure, for example, around the optimal solution, for high dimensional problems. Then a corresponding "objective-oriented experimental design" is proposed in order to make the generated surrogate $s(x)$ better suitable for the accurate calculation of the proposed specific local sensitivity quantities. In addition, we demonstrate the better performance of the Gaussian radial basis function interpolator over Kriging in our cases, which are of relatively high dimensionality and few experimental design points. Numerical experiments demonstrate that the optimization procedure and the "objective-oriented experimental design" behavior much better than the classical Latin Hypercube Design. In addition, the performance of Kriging is not as good as Gaussian RBF, especially in the case of high dimensional problems.
A General Stochastic Algorithmic Framework for Minimizing Expensive Black Box Objective Functions Based on Surrogate Models and Sensitivity Analysis
Oct 23, 2014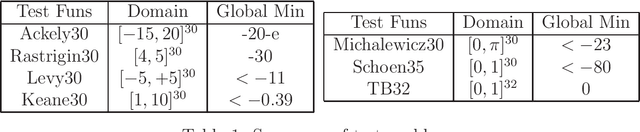
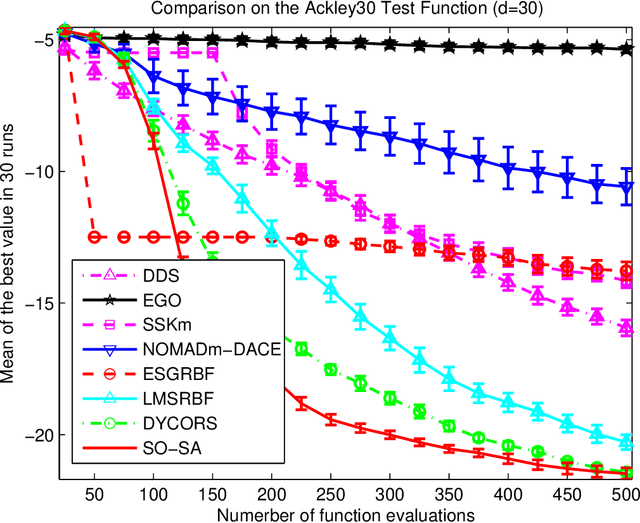
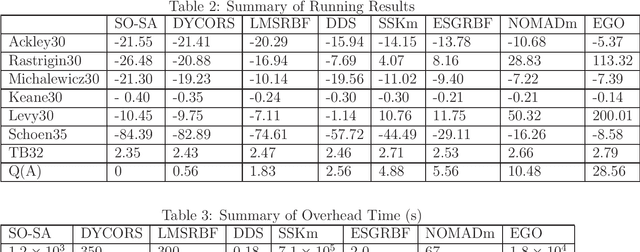
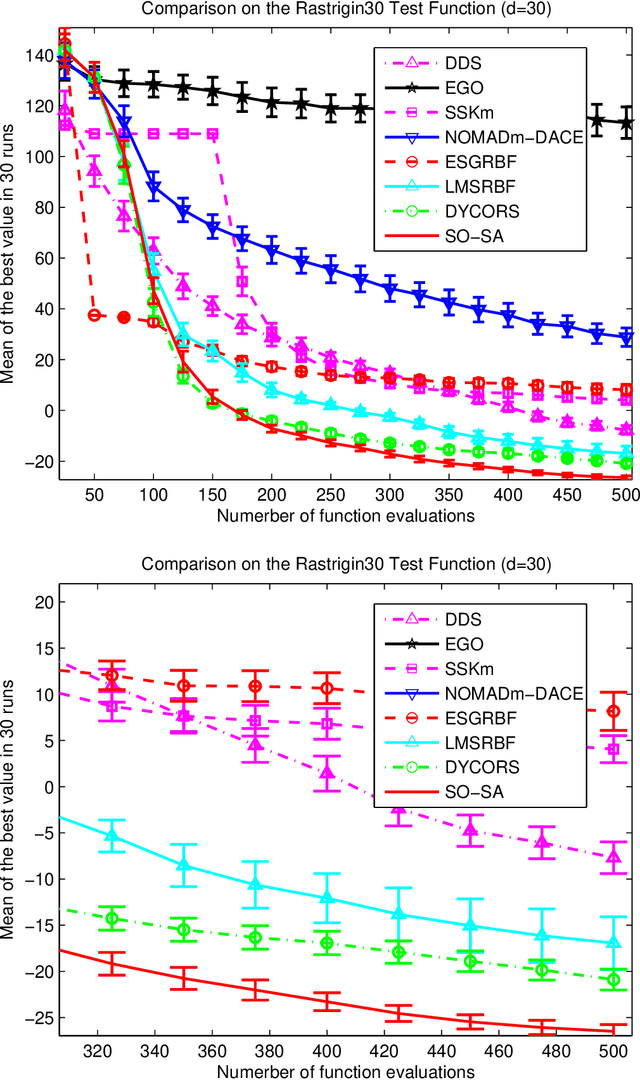
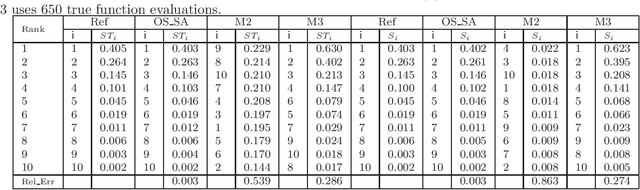
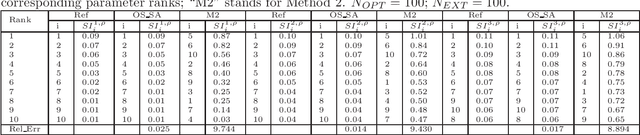
Abstract:We are focusing on bound constrained global optimization problems, whose objective functions are computationally expensive black-box functions and have multiple local minima. The recently popular Metric Stochastic Response Surface (MSRS) algorithm proposed by \cite{Regis2007SRBF} based on adaptive or sequential learning based on response surfaces is revisited and further extended for better performance in case of higher dimensional problems. Specifically, we propose a new way to generate the candidate points which the next function evaluation point is picked from according to the metric criteria, based on a new definition of distance, and prove the global convergence of the corresponding. Correspondingly, a more adaptive implementation of MSRS, named "SO-SA", is presented. "SO-SA" is is more likely to perturb those most sensitive coordinates when generating the candidate points, instead of perturbing all coordinates simultaneously. Numerical experiments on both synthetic problems and real problems demonstrate the advantages of our new algorithm, compared with many state of the art alternatives.}
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge