A General Stochastic Algorithmic Framework for Minimizing Expensive Black Box Objective Functions Based on Surrogate Models and Sensitivity Analysis
Paper and Code
Oct 23, 2014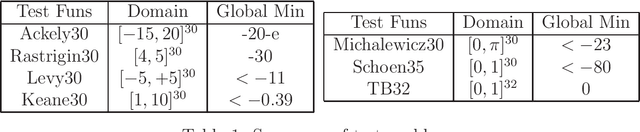
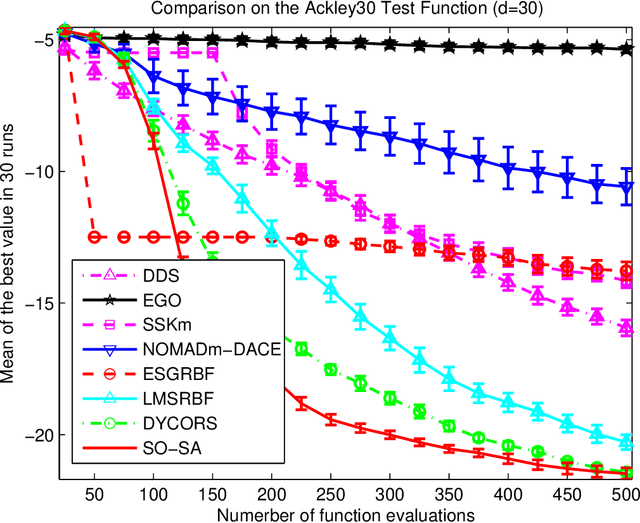
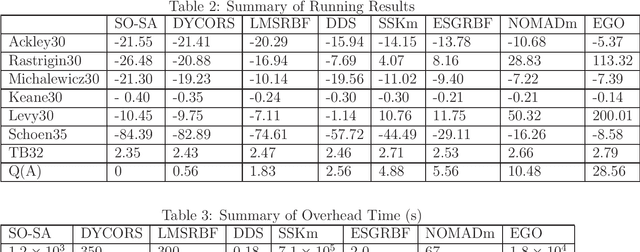
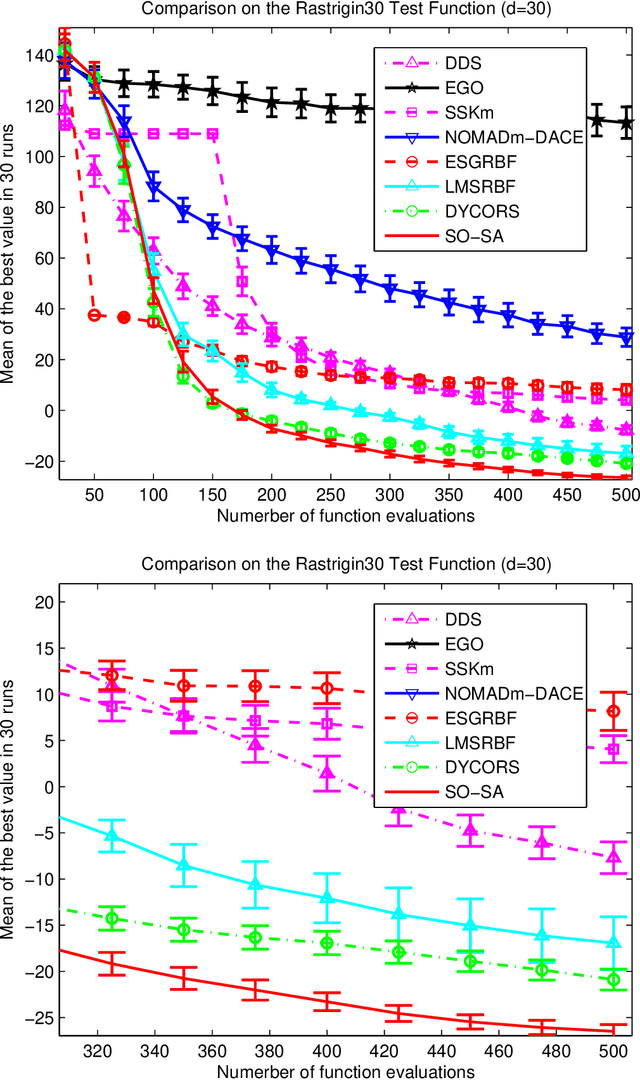
We are focusing on bound constrained global optimization problems, whose objective functions are computationally expensive black-box functions and have multiple local minima. The recently popular Metric Stochastic Response Surface (MSRS) algorithm proposed by \cite{Regis2007SRBF} based on adaptive or sequential learning based on response surfaces is revisited and further extended for better performance in case of higher dimensional problems. Specifically, we propose a new way to generate the candidate points which the next function evaluation point is picked from according to the metric criteria, based on a new definition of distance, and prove the global convergence of the corresponding. Correspondingly, a more adaptive implementation of MSRS, named "SO-SA", is presented. "SO-SA" is is more likely to perturb those most sensitive coordinates when generating the candidate points, instead of perturbing all coordinates simultaneously. Numerical experiments on both synthetic problems and real problems demonstrate the advantages of our new algorithm, compared with many state of the art alternatives.}
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge