Sensitivity Analysis for Computationally Expensive Models using Optimization and Objective-oriented Surrogate Approximations
Paper and Code
Feb 21, 2015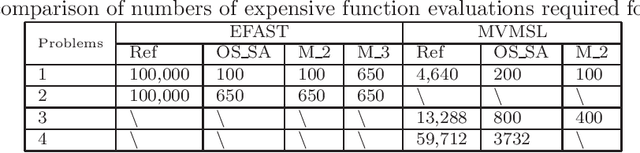
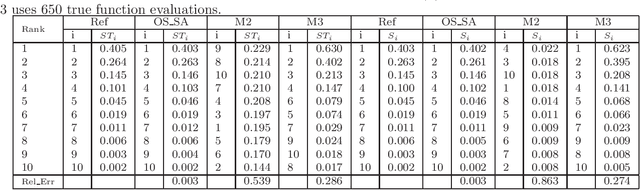
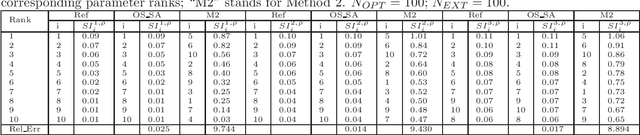

In this paper, we focus on developing efficient sensitivity analysis methods for a computationally expensive objective function $f(x)$ in the case that the minimization of it has just been performed. Here "computationally expensive" means that each of its evaluation takes significant amount of time, and therefore our main goal to use a small number of function evaluations of $f(x)$ to further infer the sensitivity information of these different parameters. Correspondingly, we consider the optimization procedure as an adaptive experimental design and re-use its available function evaluations as the initial design points to establish a surrogate model $s(x)$ (or called response surface). The sensitivity analysis is performed on $s(x)$, which is an lieu of $f(x)$. Furthermore, we propose a new local multivariate sensitivity measure, for example, around the optimal solution, for high dimensional problems. Then a corresponding "objective-oriented experimental design" is proposed in order to make the generated surrogate $s(x)$ better suitable for the accurate calculation of the proposed specific local sensitivity quantities. In addition, we demonstrate the better performance of the Gaussian radial basis function interpolator over Kriging in our cases, which are of relatively high dimensionality and few experimental design points. Numerical experiments demonstrate that the optimization procedure and the "objective-oriented experimental design" behavior much better than the classical Latin Hypercube Design. In addition, the performance of Kriging is not as good as Gaussian RBF, especially in the case of high dimensional problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge