Efficient Multi-Objective Optimization through Population-based Parallel Surrogate Search

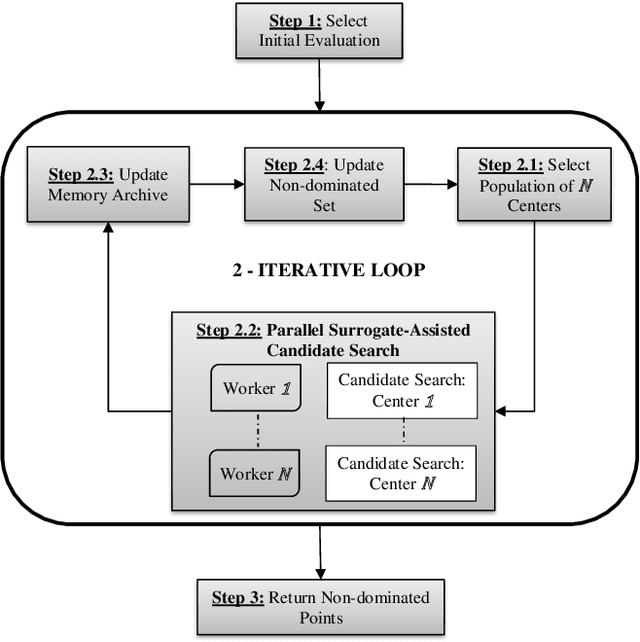
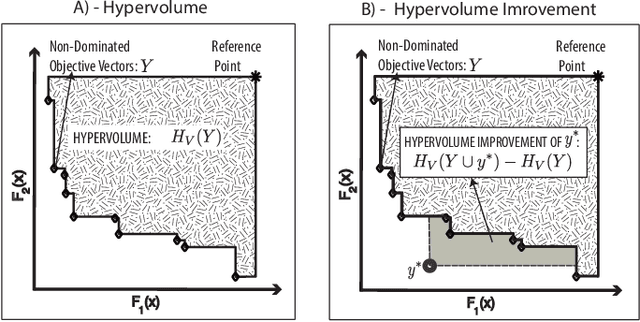
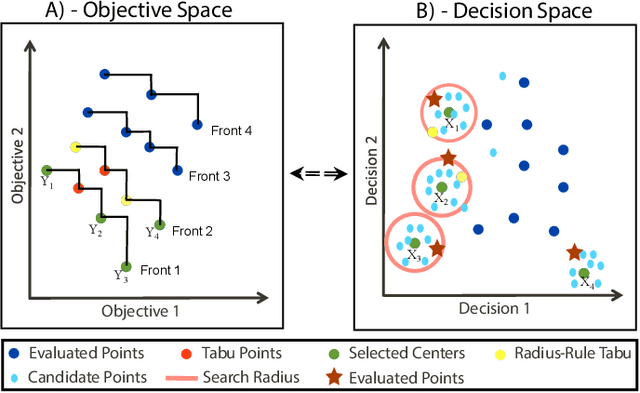
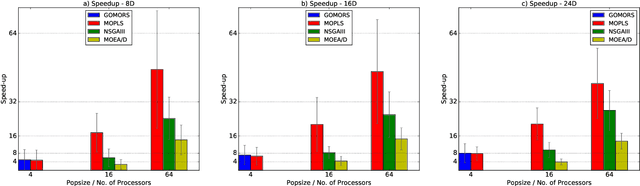
Multi-Objective Optimization (MOO) is very difficult for expensive functions because most current MOO methods rely on a large number of function evaluations to get an accurate solution. We address this problem with surrogate approximation and parallel computation. We develop an MOO algorithm MOPLS-N for expensive functions that combines iteratively updated surrogate approximations of the objective functions with a structure for efficiently selecting a population of $N$ points so that the expensive objectives for all points are simultaneously evaluated on $N$ processors in each iteration. MOPLS incorporates Radial Basis Function (RBF) approximation, Tabu Search and local candidate search around multiple points to strike a balance between exploration, exploitation and diversification during each algorithm iteration. Eleven test problems (with 8 to 24 decision variables and two real-world watershed problems are used to compare performance of MOPLS to ParEGO, GOMORS, Borg, MOEA/D, and NSGA-III on a limited budget of evaluations with between 1 (serial) and 64 processors. MOPLS in serial is better than all non-RBF serial methods tested. Parallel speedup of MOPLS is higher than all other parallel algorithms with 16 and 64 processors. With both algorithms on 64 processors MOPLS is at least 2 times faster than NSGA-III on the watershed problems.

Efficient Hyperparameter Optimization of Deep Learning Algorithms Using Deterministic RBF Surrogates

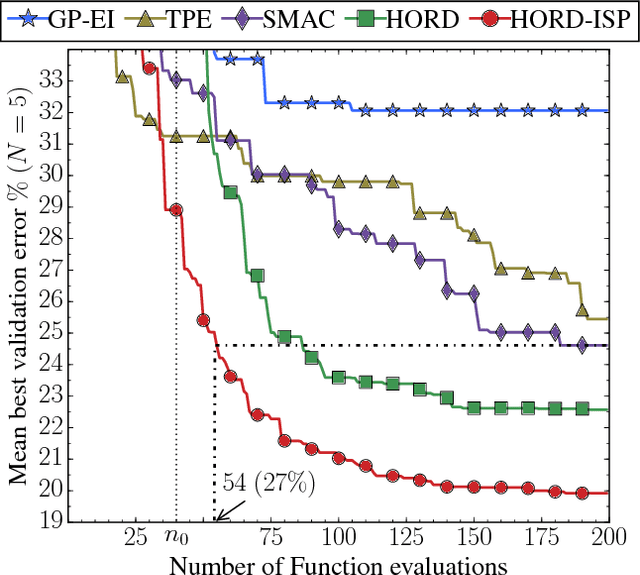
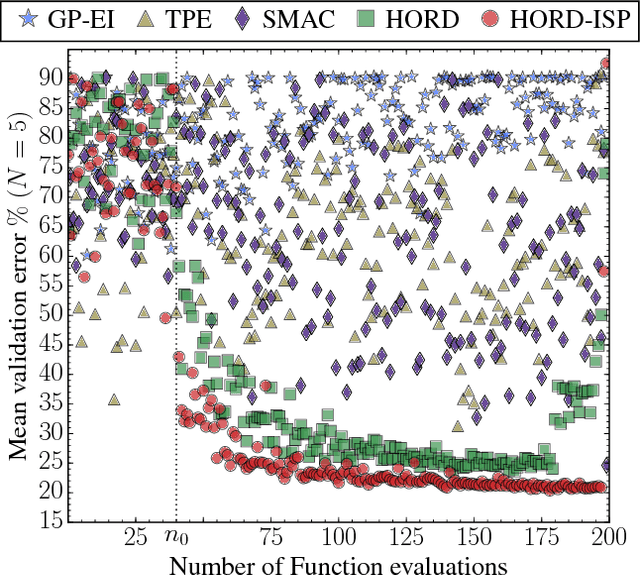
Automatically searching for optimal hyperparameter configurations is of crucial importance for applying deep learning algorithms in practice. Recently, Bayesian optimization has been proposed for optimizing hyperparameters of various machine learning algorithms. Those methods adopt probabilistic surrogate models like Gaussian processes to approximate and minimize the validation error function of hyperparameter values. However, probabilistic surrogates require accurate estimates of sufficient statistics (e.g., covariance) of the error distribution and thus need many function evaluations with a sizeable number of hyperparameters. This makes them inefficient for optimizing hyperparameters of deep learning algorithms, which are highly expensive to evaluate. In this work, we propose a new deterministic and efficient hyperparameter optimization method that employs radial basis functions as error surrogates. The proposed mixed integer algorithm, called HORD, searches the surrogate for the most promising hyperparameter values through dynamic coordinate search and requires many fewer function evaluations. HORD does well in low dimensions but it is exceptionally better in higher dimensions. Extensive evaluations on MNIST and CIFAR-10 for four deep neural networks demonstrate HORD significantly outperforms the well-established Bayesian optimization methods such as GP, SMAC, and TPE. For instance, on average, HORD is more than 6 times faster than GP-EI in obtaining the best configuration of 19 hyperparameters.