Efficient Multi-Objective Optimization through Population-based Parallel Surrogate Search
Paper and Code
Mar 06, 2019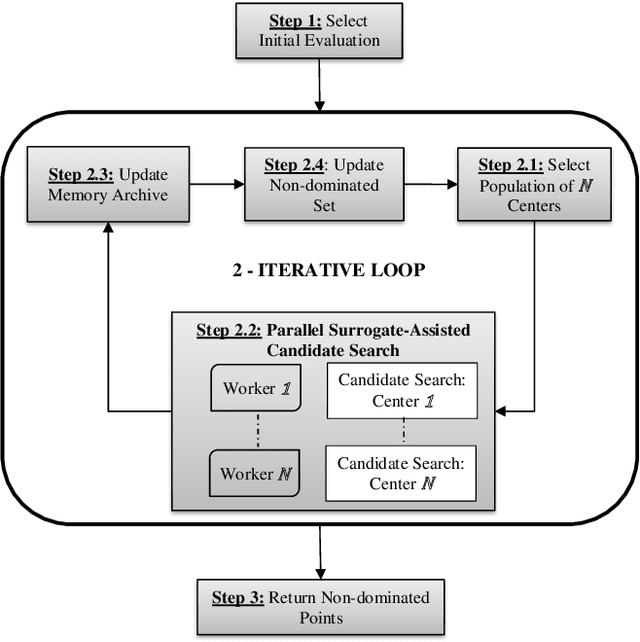
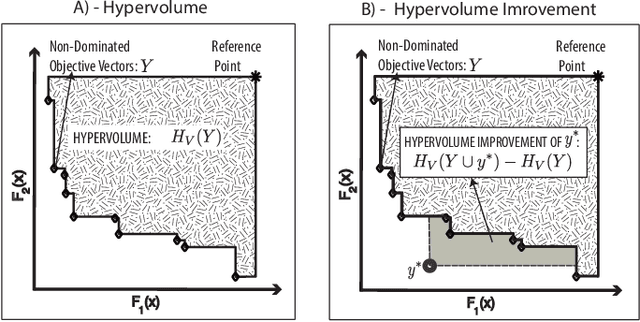
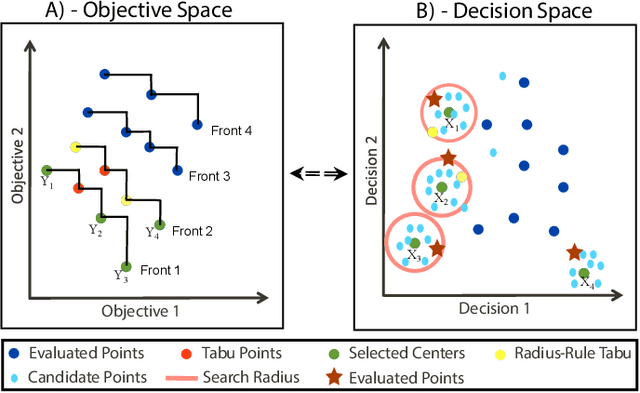
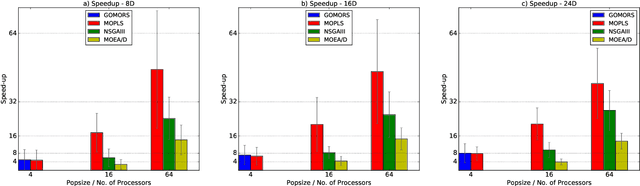
Multi-Objective Optimization (MOO) is very difficult for expensive functions because most current MOO methods rely on a large number of function evaluations to get an accurate solution. We address this problem with surrogate approximation and parallel computation. We develop an MOO algorithm MOPLS-N for expensive functions that combines iteratively updated surrogate approximations of the objective functions with a structure for efficiently selecting a population of $N$ points so that the expensive objectives for all points are simultaneously evaluated on $N$ processors in each iteration. MOPLS incorporates Radial Basis Function (RBF) approximation, Tabu Search and local candidate search around multiple points to strike a balance between exploration, exploitation and diversification during each algorithm iteration. Eleven test problems (with 8 to 24 decision variables and two real-world watershed problems are used to compare performance of MOPLS to ParEGO, GOMORS, Borg, MOEA/D, and NSGA-III on a limited budget of evaluations with between 1 (serial) and 64 processors. MOPLS in serial is better than all non-RBF serial methods tested. Parallel speedup of MOPLS is higher than all other parallel algorithms with 16 and 64 processors. With both algorithms on 64 processors MOPLS is at least 2 times faster than NSGA-III on the watershed problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge