AlphaFold Distillation for Improved Inverse Protein Folding

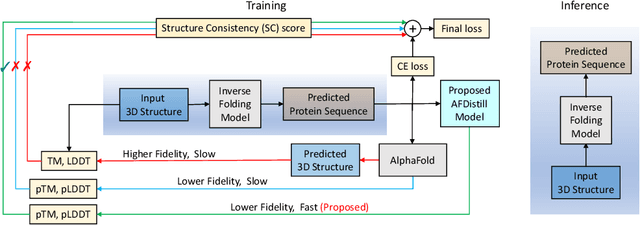
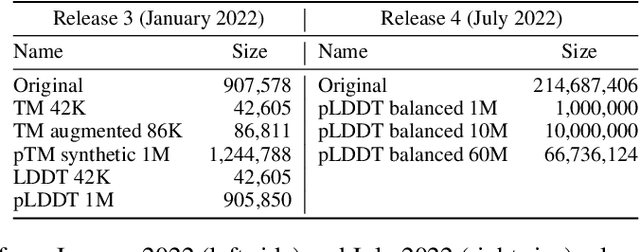
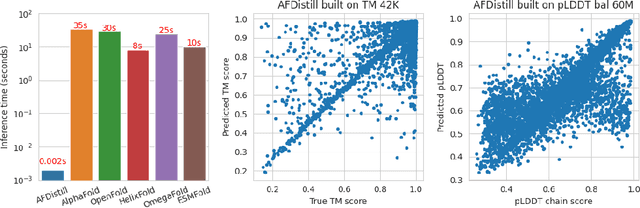
Inverse protein folding, i.e., designing sequences that fold into a given three-dimensional structure, is one of the fundamental design challenges in bio-engineering and drug discovery. Traditionally, inverse folding mainly involves learning from sequences that have an experimentally resolved structure. However, the known structures cover only a tiny space of the protein sequences, imposing limitations on the model learning. Recently proposed forward folding models, e.g., AlphaFold, offer unprecedented opportunity for accurate estimation of the structure given a protein sequence. Naturally, incorporating a forward folding model as a component of an inverse folding approach offers the potential of significantly improving the inverse folding, as the folding model can provide a feedback on any generated sequence in the form of the predicted protein structure or a structural confidence metric. However, at present, these forward folding models are still prohibitively slow to be a part of the model optimization loop during training. In this work, we propose to perform knowledge distillation on the folding model's confidence metrics, e.g., pTM or pLDDT scores, to obtain a smaller, faster and end-to-end differentiable distilled model, which then can be included as part of the structure consistency regularized inverse folding model training. Moreover, our regularization technique is general enough and can be applied in other design tasks, e.g., sequence-based protein infilling. Extensive experiments show a clear benefit of our method over the non-regularized baselines. For example, in inverse folding design problems we observe up to 3% improvement in sequence recovery and up to 45% improvement in protein diversity, while still preserving structural consistency of the generated sequences.

Protein Representation Learning by Geometric Structure Pretraining

Learning effective protein representations is critical in a variety of tasks in biology such as predicting protein function or structure. Existing approaches usually pretrain protein language models on a large number of unlabeled amino acid sequences and then finetune the models with some labeled data in downstream tasks. Despite the effectiveness of sequence-based approaches, the power of pretraining on smaller numbers of known protein structures has not been explored for protein property prediction, though protein structures are known to be determinants of protein function. We first present a simple yet effective encoder to learn protein geometry features. We pretrain the protein graph encoder by leveraging multiview contrastive learning and different self-prediction tasks. Experimental results on both function prediction and fold classification tasks show that our proposed pretraining methods outperform or are on par with the state-of-the-art sequence-based methods using much less data. All codes and models will be published upon acceptance.

Benchmarking deep generative models for diverse antibody sequence design

Computational protein design, i.e. inferring novel and diverse protein sequences consistent with a given structure, remains a major unsolved challenge. Recently, deep generative models that learn from sequences alone or from sequences and structures jointly have shown impressive performance on this task. However, those models appear limited in terms of modeling structural constraints, capturing enough sequence diversity, or both. Here we consider three recently proposed deep generative frameworks for protein design: (AR) the sequence-based autoregressive generative model, (GVP) the precise structure-based graph neural network, and Fold2Seq that leverages a fuzzy and scale-free representation of a three-dimensional fold, while enforcing structure-to-sequence (and vice versa) consistency. We benchmark these models on the task of computational design of antibody sequences, which demand designing sequences with high diversity for functional implication. The Fold2Seq framework outperforms the two other baselines in terms of diversity of the designed sequences, while maintaining the typical fold.

On Extensions of CLEVER: A Neural Network Robustness Evaluation Algorithm

CLEVER (Cross-Lipschitz Extreme Value for nEtwork Robustness) is an Extreme Value Theory (EVT) based robustness score for large-scale deep neural networks (DNNs). In this paper, we propose two extensions on this robustness score. First, we provide a new formal robustness guarantee for classifier functions that are twice differentiable. We apply extreme value theory on the new formal robustness guarantee and the estimated robustness is called second-order CLEVER score. Second, we discuss how to handle gradient masking, a common defensive technique, using CLEVER with Backward Pass Differentiable Approximation (BPDA). With BPDA applied, CLEVER can evaluate the intrinsic robustness of neural networks of a broader class -- networks with non-differentiable input transformations. We demonstrate the effectiveness of CLEVER with BPDA in experiments on a 121-layer Densenet model trained on the ImageNet dataset.

A General Family of Trimmed Estimators for Robust High-dimensional Data Analysis

We consider the problem of robustifying high-dimensional structured estimation. Robust techniques are key in real-world applications which often involve outliers and data corruption. We focus on trimmed versions of structurally regularized M-estimators in the high-dimensional setting, including the popular Least Trimmed Squares estimator, as well as analogous estimators for generalized linear models and graphical models, using possibly non-convex loss functions. We present a general analysis of their statistical convergence rates and consistency, and then take a closer look at the trimmed versions of the Lasso and Graphical Lasso estimators as special cases. On the optimization side, we show how to extend algorithms for M-estimators to fit trimmed variants and provide guarantees on their numerical convergence. The generality and competitive performance of high-dimensional trimmed estimators are illustrated numerically on both simulated and real-world genomics data.

Neurogenesis-Inspired Dictionary Learning: Online Model Adaption in a Changing World

In this paper, we focus on online representation learning in non-stationary environments which may require continuous adaptation of model architecture. We propose a novel online dictionary-learning (sparse-coding) framework which incorporates the addition and deletion of hidden units (dictionary elements), and is inspired by the adult neurogenesis phenomenon in the dentate gyrus of the hippocampus, known to be associated with improved cognitive function and adaptation to new environments. In the online learning setting, where new input instances arrive sequentially in batches, the neuronal-birth is implemented by adding new units with random initial weights (random dictionary elements); the number of new units is determined by the current performance (representation error) of the dictionary, higher error causing an increase in the birth rate. Neuronal-death is implemented by imposing l1/l2-regularization (group sparsity) on the dictionary within the block-coordinate descent optimization at each iteration of our online alternating minimization scheme, which iterates between the code and dictionary updates. Finally, hidden unit connectivity adaptation is facilitated by introducing sparsity in dictionary elements. Our empirical evaluation on several real-life datasets (images and language) as well as on synthetic data demonstrates that the proposed approach can considerably outperform the state-of-art fixed-size (nonadaptive) online sparse coding of Mairal et al. (2009) in the presence of nonstationary data. Moreover, we identify certain properties of the data (e.g., sparse inputs with nearly non-overlapping supports) and of the model (e.g., dictionary sparsity) associated with such improvements.

Scalable Matrix-valued Kernel Learning for High-dimensional Nonlinear Multivariate Regression and Granger Causality

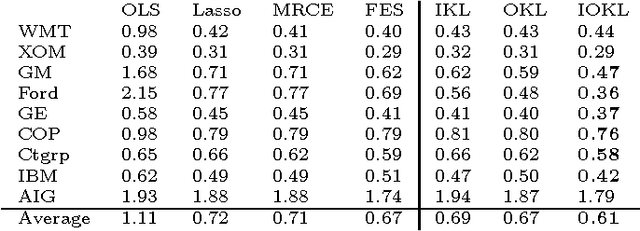
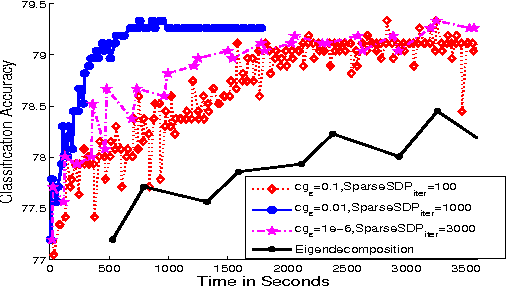
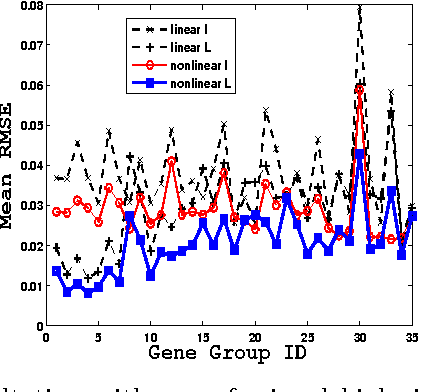
We propose a general matrix-valued multiple kernel learning framework for high-dimensional nonlinear multivariate regression problems. This framework allows a broad class of mixed norm regularizers, including those that induce sparsity, to be imposed on a dictionary of vector-valued Reproducing Kernel Hilbert Spaces. We develop a highly scalable and eigendecomposition-free algorithm that orchestrates two inexact solvers for simultaneously learning both the input and output components of separable matrix-valued kernels. As a key application enabled by our framework, we show how high-dimensional causal inference tasks can be naturally cast as sparse function estimation problems, leading to novel nonlinear extensions of a class of Graphical Granger Causality techniques. Our algorithmic developments and extensive empirical studies are complemented by theoretical analyses in terms of Rademacher generalization bounds.