An Automated Tape Laying System Employing a Uniaxial Force Control Device

This paper deals with the design of a cost effective automated tape laying system (ATL system) with integrated uniaxial force control to ensure the necessary compaction forces as well as with an accurate temperature control to guarantee the used tape being melted appropriate. It is crucial to control the substrate and the oncoming tape onto a specific temperature level to ensure an optimal consolidation between the different layers of the product. Therefore, it takes several process steps from the spooled tape on the coil until it is finally tacked onto the desired mold. The different modules are divided into the tape storage spool, a tape-guiding roller, a tape processing unit, a heating zone and the consolidation unit. Moreover, a special robot control concept for testing the ATL system is presented. In contrast to many other systems, with this approach, the tape laying device is spatially fixed and the shape is moved accordingly by the robot, which allows for handling of rather compact and complex shapes. The functionality of the subsystems and the taping process itself was finally approved in experimental results using a carbon fiber reinforced HDPE tape.

A Parameter-Linear Formulation of the Optimal Path Following Problem for Robotic Manipulator

In this paper the computational challenges of time-optimal path following are addressed. The standard approach is to minimize the travel time, which inevitably leads to singularities at zero path speed, when reformulating the optimization problem in terms of a path parameter. Thus, smooth trajectory generation while maintaining a low computational effort is quite challenging, since the singularities have to be taken into account. To this end, a different approach is presented in this paper. This approach is based on maximizing the path speed along a prescribed path. Furthermore, the approach is capable of planning smooth trajectories numerically efficient. Moreover, the discrete reformulation of the underlying problem is linear in optimization variables.

Robot Path and Trajectory Planning Considering a Spatially Fixed TCP

This paper presents a method for planning a trajectory in workspace coordinates using a spatially fixed tool center point (TCP), while taking into account the processing path on a part. This approach is beneficial if it is easier to move the part rather than moving the tool. Whether a mathematical description that defines the shape to be processed or single points from a design program are used, the robot path is finally represented using B-splines. The use of splines enables the path to be continuous with a desired degree, which finally leads to a smooth robot trajectory. While calculating the robot trajectory through prescribed orientation, additionally a given velocity at the TCP has to be considered. The procedure was validated on a real system using an industrial robot moving an arbitrary defined part.

Simultaneous Stiffness and Trajectory Optimization for Energy Minimization of Pick-and-Place Tasks of SEA-Actuated Parallel Kinematic Manipulators

A major field of industrial robot applications deals with repetitive tasks that alternate between operating points. For these so-called pick-and-place operations, parallel kinematic manipulators (PKM) are frequently employed. These tasks tend to automatically run for a long period of time and therefore minimizing energy consumption is always of interest. Recent research addresses this topic by the use of elastic elements and particularly series elastic actuators (SEA). This paper explores the possibilities of minimizing energy consumption of SEA actuated PKM performing pick-and-place tasks. The basic idea is to excite eigenmotions that result from the actuator springs and exploit their oscillating characteristics. To this end, a prescribed cyclic pick-and-place operation is analyzed and a dynamic model of SEA driven PKM is derived. Subsequently, an energy minimizing optimal control problem is formulated where operating trajectories as well as SEA stiffnesses are optimized simultaneously. Here, optimizing the actuator stiffness does not account for variable stiffness actuators. It serves as a tool for the design and dimensioning process. The hypothesis on energy reduction is tested on two (parallel) robot applications where redundant actuation is also addressed. The results confirm the validity of this approach.

Wohlhart's Three-Loop Mechanism: An Overconstrained and Shaky Linkage

This paper revisits a three-loop spatial linkage that was proposed in an ARK 2004 paper by Karl Wohlhart (as extension of a two-loop linkage proposed by Eddie Baker in 1980) and later analyzed in an ARK 2006 paper by Diez-Martinez et. al. A local analysis shows that this linkage has a finite degree of freedom (DOF) 3 (and is thus overconstrained) while in its reference configuration the differential DOF is 5. It is shown that its configuration space is locally a smooth manifold so that the reference configuration is not a c-space singularity. It is shown that the differential DOF is locally constant, which makes this linkage shaky (so that the reference configuration is not a singularity). The higher-order local analysis is facilitated by the computation of the kinematic tangent cone as well as a local approximation of the c-space.

An $O(n$)-Algorithm for the Higher-Order Kinematics and Inverse Dynamics of Serial Manipulators using Spatial Representation of Twists

Optimal control in general, and flatness-based control in particular, of robotic arms necessitate to compute the first and second time derivatives of the joint torques/forces required to achieve a desired motion. In view of the required computational efficiency, recursive $O(n)$-algorithms were proposed to this end. Aiming at compact yet efficient formulations, a Lie group formulation was recently proposed, making use of body-fixed and hybrid representation of twists and wrenches. In this paper a formulation is introduced using the spatial representation. The second-order inverse dynamics algorithm is accompanied by a fourth-order forward and inverse kinematics algorithm. An advantage of all Lie group formulations is that they can be parameterized in terms of vectorial quantities that are readily available. The method is demonstrated for the 7 DOF Franka Emika Panda robot.

Optimizing open-domain question answering with graph-based retrieval augmented generation

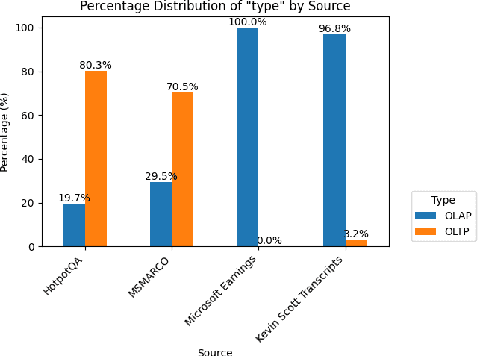
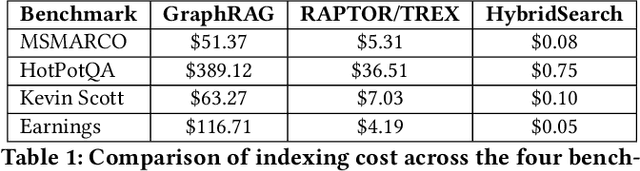
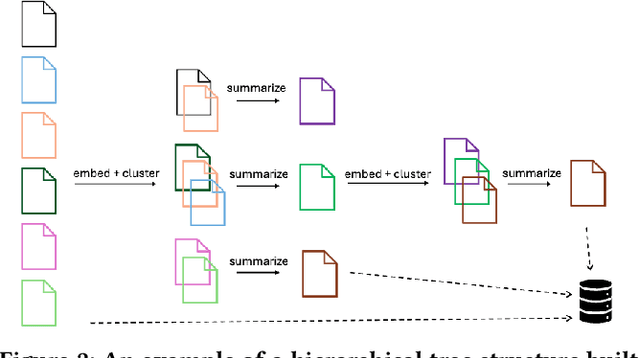
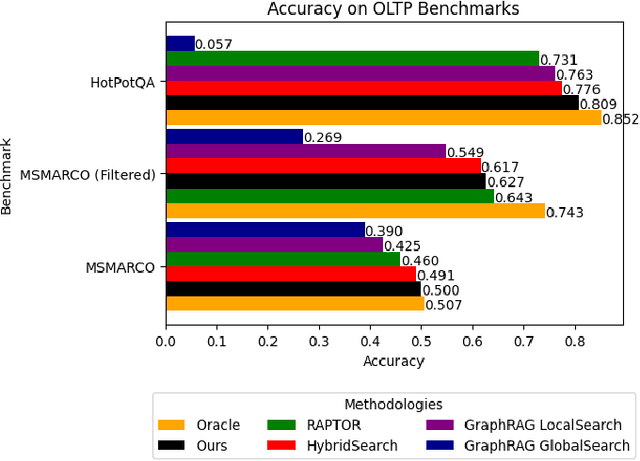
In this work, we benchmark various graph-based retrieval-augmented generation (RAG) systems across a broad spectrum of query types, including OLTP-style (fact-based) and OLAP-style (thematic) queries, to address the complex demands of open-domain question answering (QA). Traditional RAG methods often fall short in handling nuanced, multi-document synthesis tasks. By structuring knowledge as graphs, we can facilitate the retrieval of context that captures greater semantic depth and enhances language model operations. We explore graph-based RAG methodologies and introduce TREX, a novel, cost-effective alternative that combines graph-based and vector-based retrieval techniques. Our benchmarking across four diverse datasets highlights the strengths of different RAG methodologies, demonstrates TREX's ability to handle multiple open-domain QA types, and reveals the limitations of current evaluation methods. In a real-world technical support case study, we demonstrate how TREX solutions can surpass conventional vector-based RAG in efficiently synthesizing data from heterogeneous sources. Our findings underscore the potential of augmenting large language models with advanced retrieval and orchestration capabilities, advancing scalable, graph-based AI solutions.

Open Challenges in Time Series Anomaly Detection: An Industry Perspective

Current research in time-series anomaly detection is using definitions that miss critical aspects of how anomaly detection is commonly used in practice. We list several areas that are of practical relevance and that we believe are either under-investigated or missing entirely from the current discourse. Based on an investigation of systems deployed in a cloud environment, we motivate the areas of streaming algorithms, human-in-the-loop scenarios, point processes, conditional anomalies and populations analysis of time series. This paper serves as a motivation and call for action, including opportunities for theoretical and applied research, as well as for building new dataset and benchmarks.

Analytically Informed Inverse Kinematics Solution at Singularities

Near kinematic singularities of a serial manipulator, the inverse kinematics (IK) problem becomes ill-conditioned, which poses computational problems for the numerical solution. Computational methods to tackle this issue are based on various forms of a pseudoinverse (PI) solution to the velocity IK problem. The damped least squares (DLS) method provides a robust solution with controllable convergence rate. However, at singularities, it may not even be possible to solve the IK problem using any PI solution when certain end-effector motions are prescribed. To overcome this problem, an analytically informed inverse kinematics (AI-IK) method is proposed. The key step of the method is an explicit description of the tangent aspect of singular motions (the analytic part) to deduce a perturbation that yields a regular configuration. The latter serves as start configuration for the iterative solution (the numeric part). Numerical results are reported for a 7-DOF Kuka iiwa.

Dynamics of Parallel Manipulators with Hybrid Complex Limbs -- Modular Modeling and Parallel Computing

Parallel manipulators, also called parallel kinematics machines (PKM), enable robotic solutions for highly dynamic handling and machining applications. The safe and accurate design and control necessitates high-fidelity dynamics models. Such modeling approaches have already been presented for PKM with simple limbs (i.e. each limb is a serial kinematic chain). A systematic modeling approach for PKM with complex limbs (i.e. limbs that possess kinematic loops) was not yet proposed despite the fact that many successful PKM comprise complex limbs. This paper presents a systematic modular approach to the kinematics and dynamics modeling of PKM with complex limbs that are built as serial arrangement of closed loops. The latter are referred to as hybrid limbs, and can be found in almost all PKM with complex limbs, such as the Delta robot. The proposed method generalizes the formulation for PKM with simple limbs by means of local resolution of loop constraints, which is known as constraint embedding in multibody dynamics. The constituent elements of the method are the kinematic and dynamic equations of motions (EOM), and the inverse kinematics solution of the limbs, i.e. the relation of platform motion and the motion of the limbs. While the approach is conceptually independent of the used kinematics and dynamics formulation, a Lie group formulation is employed for deriving the EOM. The frame invariance of the Lie group formulation is used for devising a modular modeling method where the EOM of a representative limb are used to derived the EOM of the limbs of a particular PKM. The PKM topology is exploited in a parallel computation scheme that shall allow for computationally efficient distributed evaluation of the overall EOM of the PKM. Finally, the method is applied to the IRSBot-2 and a 3\underline{R}R[2RR]R Delta robot, which is presented in detail.