Is there an optimal choice of configuration space for Lie group integration schemes applied to constrained MBS?

Recently various numerical integration schemes have been proposed for numerically simulating the dynamics of constrained multibody systems (MBS) operating. These integration schemes operate directly on the MBS configuration space considered as a Lie group. For discrete spatial mechanical systems there are two Lie group that can be used as configuration space: $SE\left( 3\right) $ and $SO\left( 3\right) \times \mathbb{R}^{3}$. Since the performance of the numerical integration scheme clearly depends on the underlying configuration space it is important to analyze the effect of using either variant. For constrained MBS a crucial aspect is the constraint satisfaction. In this paper the constraint violation observed for the two variants are investigated. It is concluded that the $SE\left( 3\right) $ formulation outperforms the $SO\left( 3\right) \times \mathbb{R}^{3}$ formulation if the absolute motions of the rigid bodies, as part of a constrained MBS, belong to a motion subgroup. In all other cases both formulations are equivalent. In the latter cases the $SO\left( 3\right) \times \mathbb{R}^{3}$ formulation should be used since the $SE\left( 3\right) $ formulation is numerically more complex, however.

The significance of the configuration space Lie group for the constraint satisfaction in numerical time integration of multibody systems

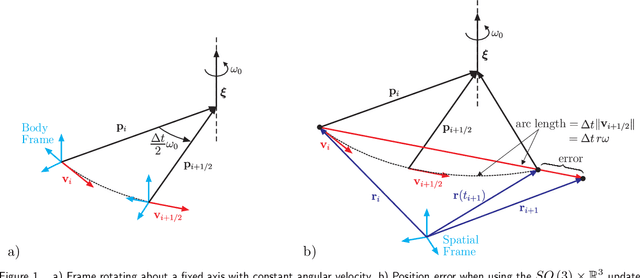
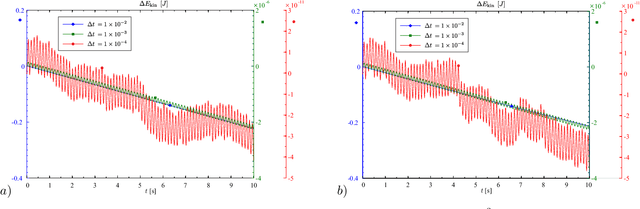
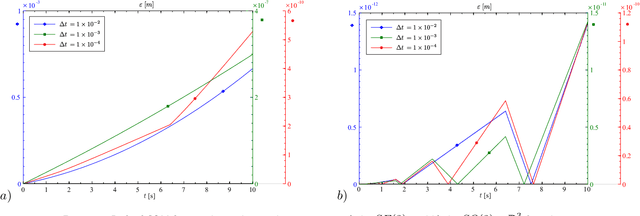
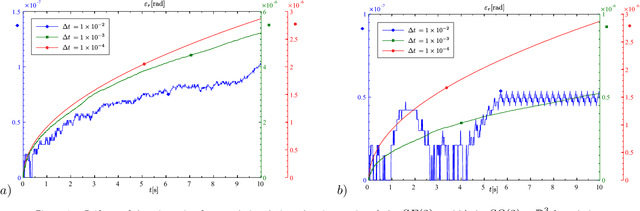
The dynamics simulation of multibody systems (MBS) using spatial velocities (non-holonomic velocities) requires time integration of the dynamics equations together with the kinematic reconstruction equations (relating time derivatives of configuration variables to rigid body velocities). The latter are specific to the geometry of the rigid body motion underlying a particular formulation, and thus to the used configuration space (c-space). The proper c-space of a rigid body is the Lie group SE(3), and the geometry is that of the screw motions. The rigid bodies within a MBS are further subjected to geometric constraints, often due to lower kinematic pairs that define SE(3) subgroups. Traditionally, however, in MBS dynamics the translations and rotations are parameterized independently, which implies the use of the direct product group $SO\left( 3\right) \times {\Bbb R}^{3}$ as rigid body c-space, although this does not account for rigid body motions. Hence, its appropriateness was recently put into perspective. In this paper the significance of the c-space for the constraint satisfaction in numerical time stepping schemes is analyzed for holonomicaly constrained MBS modeled with the 'absolute coordinate' approach, i.e. using the Newton-Euler equations for the individual bodies subjected to geometric constraints. It is shown that the geometric constraints a body is subjected to are exactly satisfied if they constrain the motion to a subgroup of its c-space. Since only the $SE\left( 3\right) $ subgroups have a practical significance it is regarded as the appropriate c-space for the constrained rigid body. Consequently the constraints imposed by lower pair joints are exactly satisfied if the joint connects a body to the ground. For a general MBS, where the motions are not constrained to a subgroup, the SE(3) and $SO\left( 3\right) \times {\Bbb R}^{3}$ yield the same order of accuracy.