Is there an optimal choice of configuration space for Lie group integration schemes applied to constrained MBS?

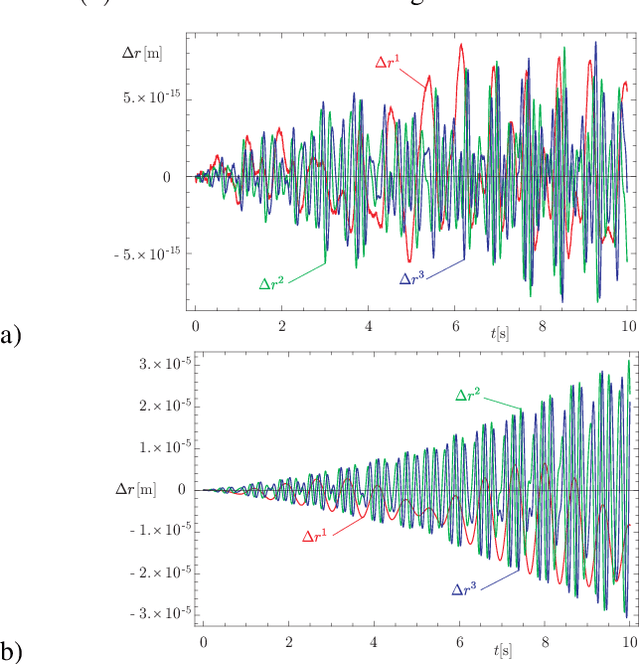
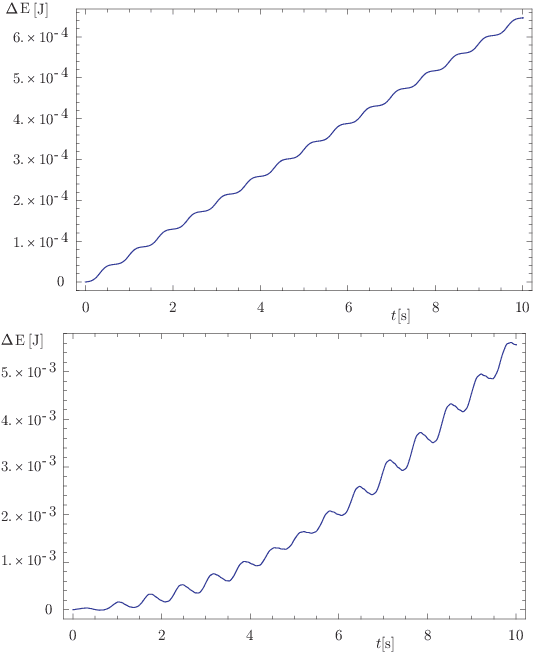
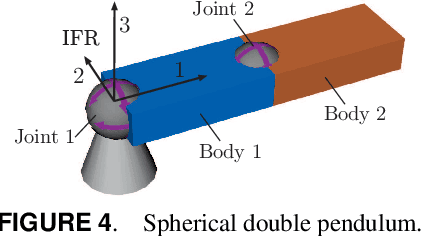
Recently various numerical integration schemes have been proposed for numerically simulating the dynamics of constrained multibody systems (MBS) operating. These integration schemes operate directly on the MBS configuration space considered as a Lie group. For discrete spatial mechanical systems there are two Lie group that can be used as configuration space: $SE\left( 3\right) $ and $SO\left( 3\right) \times \mathbb{R}^{3}$. Since the performance of the numerical integration scheme clearly depends on the underlying configuration space it is important to analyze the effect of using either variant. For constrained MBS a crucial aspect is the constraint satisfaction. In this paper the constraint violation observed for the two variants are investigated. It is concluded that the $SE\left( 3\right) $ formulation outperforms the $SO\left( 3\right) \times \mathbb{R}^{3}$ formulation if the absolute motions of the rigid bodies, as part of a constrained MBS, belong to a motion subgroup. In all other cases both formulations are equivalent. In the latter cases the $SO\left( 3\right) \times \mathbb{R}^{3}$ formulation should be used since the $SE\left( 3\right) $ formulation is numerically more complex, however.