Sub-optimality bounds for certainty equivalent policies in partially observed systems

In this paper, we present a generalization of the certainty equivalence principle of stochastic control. One interpretation of the classical certainty equivalence principle for linear systems with output feedback and quadratic costs is as follows: the optimal action at each time is obtained by evaluating the optimal state-feedback policy of the stochastic linear system at the minimum mean square error (MMSE) estimate of the state. Motivated by this interpretation, we consider certainty equivalent policies for general (non-linear) partially observed stochastic systems that allow for any state estimate rather than restricting to MMSE estimates. In such settings, the certainty equivalent policy is not optimal. For models where the cost and the dynamics are smooth in an appropriate sense, we derive upper bounds on the sub-optimality of certainty equivalent policies. We present several examples to illustrate the results.

Task load dependent decision referrals for joint binary classification in human-automation teams

We consider the problem of optimal decision referrals in human-automation teams performing binary classification tasks. The automation, which includes a pre-trained classifier, observes data for a batch of independent tasks, analyzes them, and may refer a subset of tasks to a human operator for fresh and final analysis. Our key modeling assumption is that human performance degrades with task load. We model the problem of choosing which tasks to refer as a stochastic optimization problem and show that, for a given task load, it is optimal to myopically refer tasks that yield the largest reduction in expected cost, conditional on the observed data. This provides a ranking scheme and a policy to determine the optimal set of tasks for referral. We evaluate this policy against a baseline through an experimental study with human participants. Using a radar screen simulator, participants made binary target classification decisions under time constraint. They were guided by a decision rule provided to them, but were still prone to errors under time pressure. An initial experiment estimated human performance model parameters, while a second experiment compared two referral policies. Results show statistically significant gains for the proposed optimal referral policy over a blind policy that determines referrals using the automation and human-performance models but not based on the observed data.

A Theoretical Justification for Asymmetric Actor-Critic Algorithms

In reinforcement learning for partially observable environments, many successful algorithms were developed within the asymmetric learning paradigm. This paradigm leverages additional state information available at training time for faster learning. Although the proposed learning objectives are usually theoretically sound, these methods still lack a theoretical justification for their potential benefits. We propose such a justification for asymmetric actor-critic algorithms with linear function approximators by adapting a finite-time convergence analysis to this setting. The resulting finite-time bound reveals that the asymmetric critic eliminates an error term arising from aliasing in the agent state.

Concentration of Cumulative Reward in Markov Decision Processes

In this paper, we investigate the concentration properties of cumulative rewards in Markov Decision Processes (MDPs), focusing on both asymptotic and non-asymptotic settings. We introduce a unified approach to characterize reward concentration in MDPs, covering both infinite-horizon settings (i.e., average and discounted reward frameworks) and finite-horizon setting. Our asymptotic results include the law of large numbers, the central limit theorem, and the law of iterated logarithms, while our non-asymptotic bounds include Azuma-Hoeffding-type inequalities and a non-asymptotic version of the law of iterated logarithms. Additionally, we explore two key implications of our results. First, we analyze the sample path behavior of the difference in rewards between any two stationary policies. Second, we show that two alternative definitions of regret for learning policies proposed in the literature are rate-equivalent. Our proof techniques rely on a novel martingale decomposition of cumulative rewards, properties of the solution to the policy evaluation fixed-point equation, and both asymptotic and non-asymptotic concentration results for martingale difference sequences.

Periodic agent-state based Q-learning for POMDPs

The standard approach for Partially Observable Markov Decision Processes (POMDPs) is to convert them to a fully observed belief-state MDP. However, the belief state depends on the system model and is therefore not viable in reinforcement learning (RL) settings. A widely used alternative is to use an agent state, which is a model-free, recursively updateable function of the observation history. Examples include frame stacking and recurrent neural networks. Since the agent state is model-free, it is used to adapt standard RL algorithms to POMDPs. However, standard RL algorithms like Q-learning learn a stationary policy. Our main thesis that we illustrate via examples is that because the agent state does not satisfy the Markov property, non-stationary agent-state based policies can outperform stationary ones. To leverage this feature, we propose PASQL (periodic agent-state based Q-learning), which is a variant of agent-state-based Q-learning that learns periodic policies. By combining ideas from periodic Markov chains and stochastic approximation, we rigorously establish that PASQL converges to a cyclic limit and characterize the approximation error of the converged periodic policy. Finally, we present a numerical experiment to highlight the salient features of PASQL and demonstrate the benefit of learning periodic policies over stationary policies.

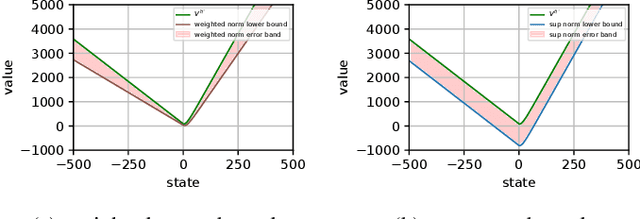
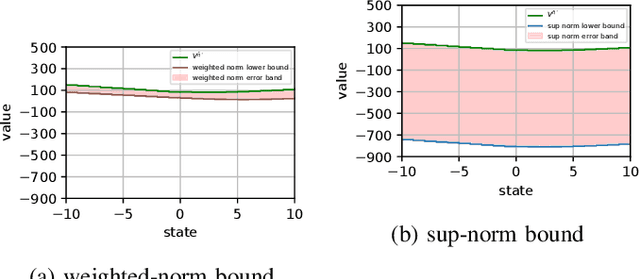
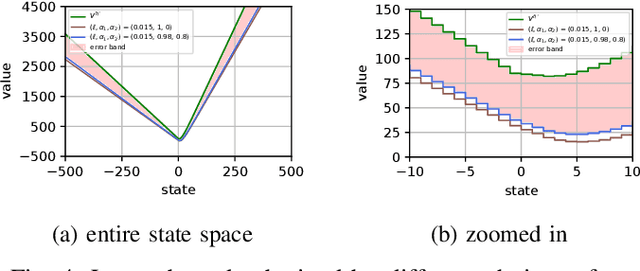
Model approximation in MDPs with unbounded per-step cost

We consider the problem of designing a control policy for an infinite-horizon discounted cost Markov decision process $\mathcal{M}$ when we only have access to an approximate model $\hat{\mathcal{M}}$. How well does an optimal policy $\hat{\pi}^{\star}$ of the approximate model perform when used in the original model $\mathcal{M}$? We answer this question by bounding a weighted norm of the difference between the value function of $\hat{\pi}^\star $ when used in $\mathcal{M}$ and the optimal value function of $\mathcal{M}$. We then extend our results and obtain potentially tighter upper bounds by considering affine transformations of the per-step cost. We further provide upper bounds that explicitly depend on the weighted distance between cost functions and weighted distance between transition kernels of the original and approximate models. We present examples to illustrate our results.

Bridging State and History Representations: Understanding Self-Predictive RL

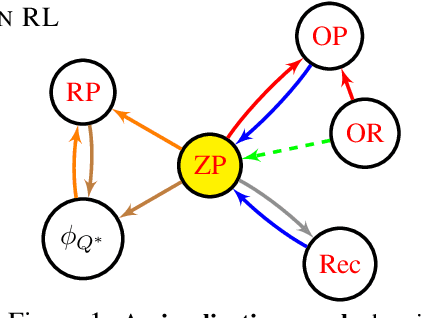
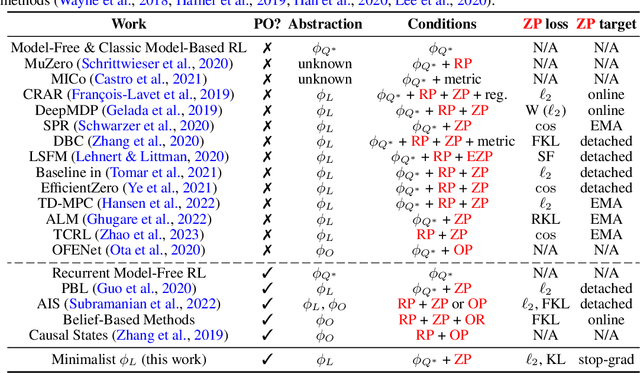
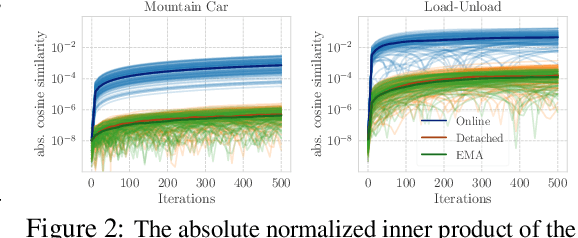
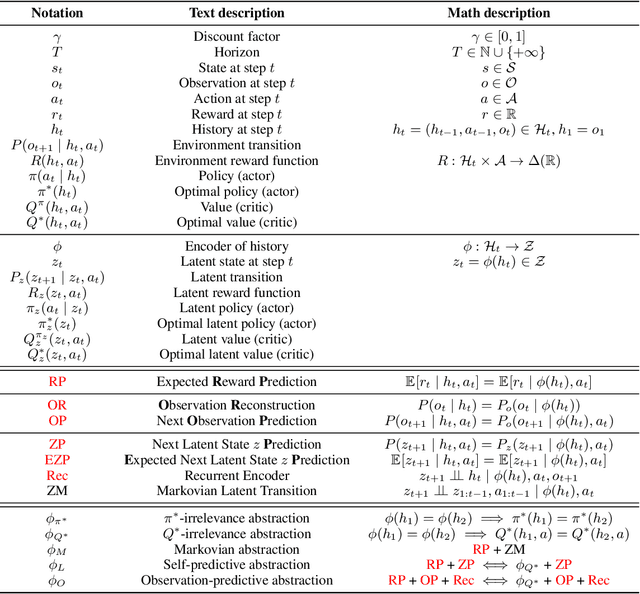
Representations are at the core of all deep reinforcement learning (RL) methods for both Markov decision processes (MDPs) and partially observable Markov decision processes (POMDPs). Many representation learning methods and theoretical frameworks have been developed to understand what constitutes an effective representation. However, the relationships between these methods and the shared properties among them remain unclear. In this paper, we show that many of these seemingly distinct methods and frameworks for state and history abstractions are, in fact, based on a common idea of self-predictive abstraction. Furthermore, we provide theoretical insights into the widely adopted objectives and optimization, such as the stop-gradient technique, in learning self-predictive representations. These findings together yield a minimalist algorithm to learn self-predictive representations for states and histories. We validate our theories by applying our algorithm to standard MDPs, MDPs with distractors, and POMDPs with sparse rewards. These findings culminate in a set of practical guidelines for RL practitioners.

Approximate information state based convergence analysis of recurrent Q-learning

In spite of the large literature on reinforcement learning (RL) algorithms for partially observable Markov decision processes (POMDPs), a complete theoretical understanding is still lacking. In a partially observable setting, the history of data available to the agent increases over time so most practical algorithms either truncate the history to a finite window or compress it using a recurrent neural network leading to an agent state that is non-Markovian. In this paper, it is shown that in spite of the lack of the Markov property, recurrent Q-learning (RQL) converges in the tabular setting. Moreover, it is shown that the quality of the converged limit depends on the quality of the representation which is quantified in terms of what is known as an approximate information state (AIS). Based on this characterization of the approximation error, a variant of RQL with AIS losses is presented. This variant performs better than a strong baseline for RQL that does not use AIS losses. It is demonstrated that there is a strong correlation between the performance of RQL over time and the loss associated with the AIS representation.

Dealing With Non-stationarity in Decentralized Cooperative Multi-Agent Deep Reinforcement Learning via Multi-Timescale Learning

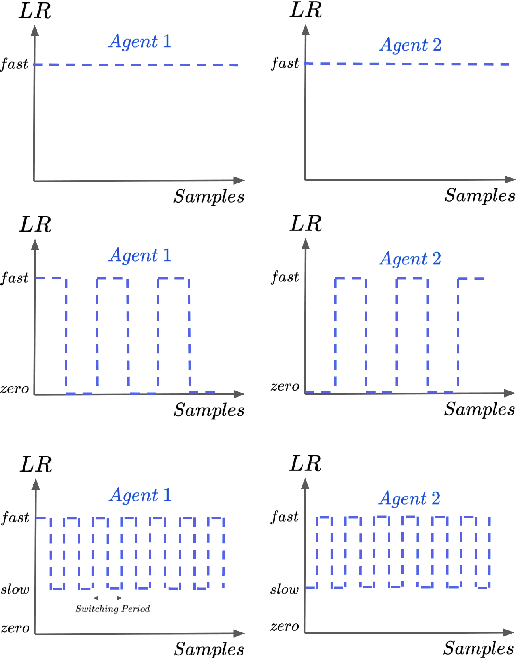
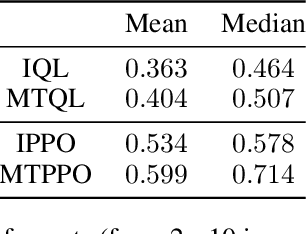
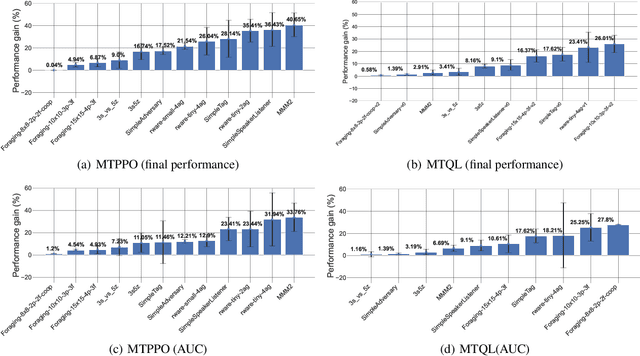
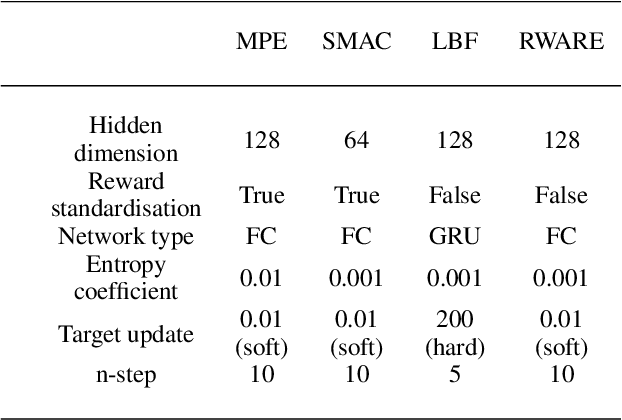
Decentralized cooperative multi-agent deep reinforcement learning (MARL) can be a versatile learning framework, particularly in scenarios where centralized training is either not possible or not practical. One of the key challenges in decentralized deep MARL is the non-stationarity of the learning environment when multiple agents are learning concurrently. A commonly used and efficient scheme for decentralized MARL is independent learning in which agents concurrently update their policies independent of each other. We first show that independent learning does not always converge, while sequential learning where agents update their policies one after another in a sequence is guaranteed to converge to an agent-by-agent optimal solution. In sequential learning, when one agent updates its policy, all other agent's policies are kept fixed, alleviating the challenge of non-stationarity due to concurrent updates in other agents' policies. However, it can be slow because only one agent is learning at any time. Therefore it might also not always be practical. In this work, we propose a decentralized cooperative MARL algorithm based on multi-timescale learning. In multi-timescale learning, all agents learn concurrently, but at different learning rates. In our proposed method, when one agent updates its policy, other agents are allowed to update their policies as well, but at a slower rate. This speeds up sequential learning, while also minimizing non-stationarity caused by other agents updating concurrently. Multi-timescale learning outperforms state-of-the-art decentralized learning methods on a set of challenging multi-agent cooperative tasks in the epymarl (papoudakis2020) benchmark. This can be seen as a first step towards more general decentralized cooperative deep MARL methods based on multi-timescale learning.

On learning history based policies for controlling Markov decision processes

Reinforcementlearning(RL)folkloresuggeststhathistory-basedfunctionapproximationmethods,suchas recurrent neural nets or history-based state abstraction, perform better than their memory-less counterparts, due to the fact that function approximation in Markov decision processes (MDP) can be viewed as inducing a Partially observable MDP. However, there has been little formal analysis of such history-based algorithms, as most existing frameworks focus exclusively on memory-less features. In this paper, we introduce a theoretical framework for studying the behaviour of RL algorithms that learn to control an MDP using history-based feature abstraction mappings. Furthermore, we use this framework to design a practical RL algorithm and we numerically evaluate its effectiveness on a set of continuous control tasks.