On learning Whittle index policy for restless bandits with scalable regret

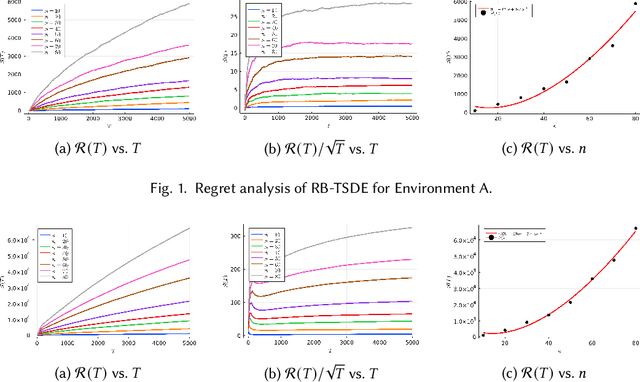
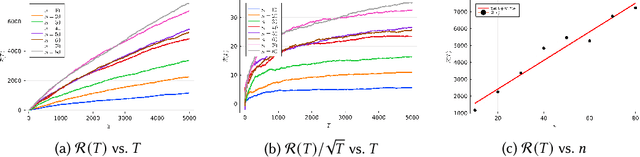
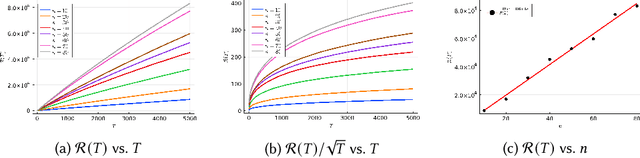
Reinforcement learning is an attractive approach to learn good resource allocation and scheduling policies based on data when the system model is unknown. However, the cumulative regret of most RL algorithms scales as $\tilde O(\mathsf{S} \sqrt{\mathsf{A} T})$, where $\mathsf{S}$ is the size of the state space, $\mathsf{A}$ is the size of the action space, $T$ is the horizon, and the $\tilde{O}(\cdot)$ notation hides logarithmic terms. Due to the linear dependence on the size of the state space, these regret bounds are prohibitively large for resource allocation and scheduling problems. In this paper, we present a model-based RL algorithm for such problem which has scalable regret. In particular, we consider a restless bandit model, and propose a Thompson-sampling based learning algorithm which is tuned to the underlying structure of the model. We present two characterizations of the regret of the proposed algorithm with respect to the Whittle index policy. First, we show that for a restless bandit with $n$ arms and at most $m$ activations at each time, the regret scales either as $\tilde{O}(mn\sqrt{T})$ or $\tilde{O}(n^2 \sqrt{T})$ depending on the reward model. Second, under an additional technical assumption, we show that the regret scales as $\tilde{O}(n^{1.5} \sqrt{T})$. We present numerical examples to illustrate the salient features of the algorithm.