Fair Resource Allocation in Weakly Coupled Markov Decision Processes

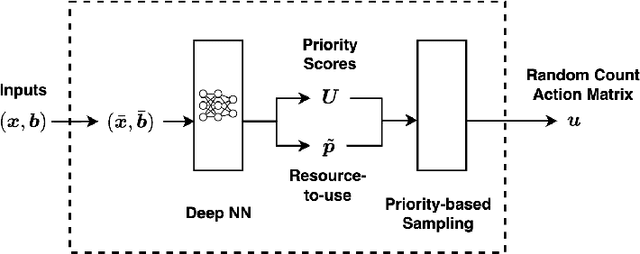
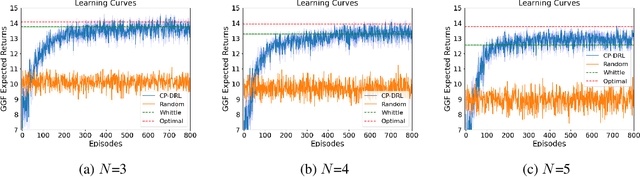
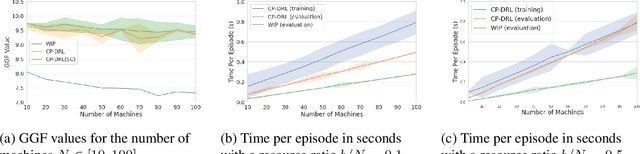
We consider fair resource allocation in sequential decision-making environments modeled as weakly coupled Markov decision processes, where resource constraints couple the action spaces of $N$ sub-Markov decision processes (sub-MDPs) that would otherwise operate independently. We adopt a fairness definition using the generalized Gini function instead of the traditional utilitarian (total-sum) objective. After introducing a general but computationally prohibitive solution scheme based on linear programming, we focus on the homogeneous case where all sub-MDPs are identical. For this case, we show for the first time that the problem reduces to optimizing the utilitarian objective over the class of "permutation invariant" policies. This result is particularly useful as we can exploit Whittle index policies in the restless bandits setting while, for the more general setting, we introduce a count-proportion-based deep reinforcement learning approach. Finally, we validate our theoretical findings with comprehensive experiments, confirming the effectiveness of our proposed method in achieving fairness.

Planning and Learning in Risk-Aware Restless Multi-Arm Bandit Problem

In restless multi-arm bandits, a central agent is tasked with optimally distributing limited resources across several bandits (arms), with each arm being a Markov decision process. In this work, we generalize the traditional restless multi-arm bandit problem with a risk-neutral objective by incorporating risk-awareness. We establish indexability conditions for the case of a risk-aware objective and provide a solution based on Whittle index. In addition, we address the learning problem when the true transition probabilities are unknown by proposing a Thompson sampling approach and show that it achieves bounded regret that scales sublinearly with the number of episodes and quadratically with the number of arms. The efficacy of our method in reducing risk exposure in restless multi-arm bandits is illustrated through a set of numerical experiments.

Approximate information state based convergence analysis of recurrent Q-learning

In spite of the large literature on reinforcement learning (RL) algorithms for partially observable Markov decision processes (POMDPs), a complete theoretical understanding is still lacking. In a partially observable setting, the history of data available to the agent increases over time so most practical algorithms either truncate the history to a finite window or compress it using a recurrent neural network leading to an agent state that is non-Markovian. In this paper, it is shown that in spite of the lack of the Markov property, recurrent Q-learning (RQL) converges in the tabular setting. Moreover, it is shown that the quality of the converged limit depends on the quality of the representation which is quantified in terms of what is known as an approximate information state (AIS). Based on this characterization of the approximation error, a variant of RQL with AIS losses is presented. This variant performs better than a strong baseline for RQL that does not use AIS losses. It is demonstrated that there is a strong correlation between the performance of RQL over time and the loss associated with the AIS representation.

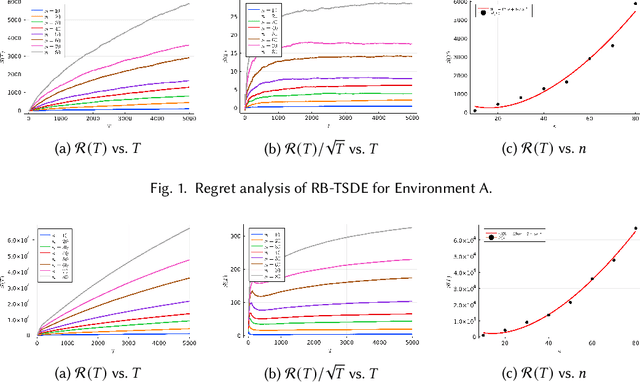
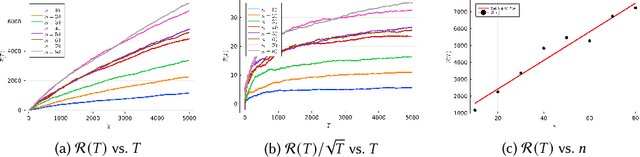
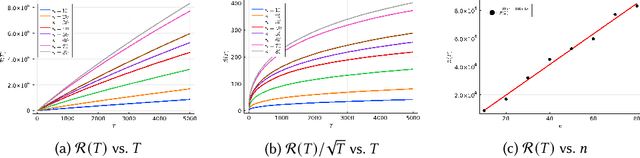
On learning Whittle index policy for restless bandits with scalable regret

Reinforcement learning is an attractive approach to learn good resource allocation and scheduling policies based on data when the system model is unknown. However, the cumulative regret of most RL algorithms scales as $\tilde O(\mathsf{S} \sqrt{\mathsf{A} T})$, where $\mathsf{S}$ is the size of the state space, $\mathsf{A}$ is the size of the action space, $T$ is the horizon, and the $\tilde{O}(\cdot)$ notation hides logarithmic terms. Due to the linear dependence on the size of the state space, these regret bounds are prohibitively large for resource allocation and scheduling problems. In this paper, we present a model-based RL algorithm for such problem which has scalable regret. In particular, we consider a restless bandit model, and propose a Thompson-sampling based learning algorithm which is tuned to the underlying structure of the model. We present two characterizations of the regret of the proposed algorithm with respect to the Whittle index policy. First, we show that for a restless bandit with $n$ arms and at most $m$ activations at each time, the regret scales either as $\tilde{O}(mn\sqrt{T})$ or $\tilde{O}(n^2 \sqrt{T})$ depending on the reward model. Second, under an additional technical assumption, we show that the regret scales as $\tilde{O}(n^{1.5} \sqrt{T})$. We present numerical examples to illustrate the salient features of the algorithm.

Scalable Operator Allocation for Multi-Robot Assistance: A Restless Bandit Approach

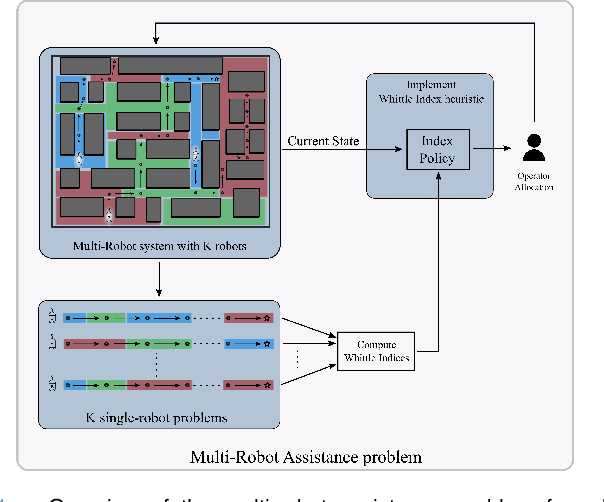
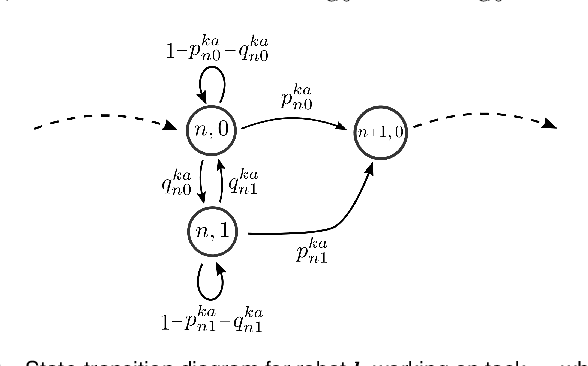
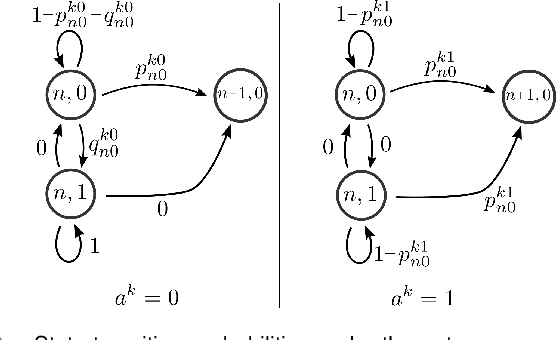
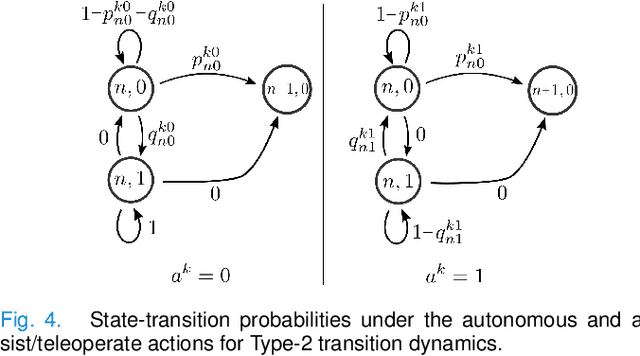
In this paper, we consider the problem of allocating human operators in a system with multiple semi-autonomous robots. Each robot is required to perform an independent sequence of tasks, subjected to a chance of failing and getting stuck in a fault state at every task. If and when required, a human operator can assist or teleoperate a robot. Conventional MDP techniques used to solve such problems face scalability issues due to exponential growth of state and action spaces with the number of robots and operators. In this paper we derive conditions under which the operator allocation problem is indexable, enabling the use of the Whittle index heuristic. The conditions can be easily checked to verify indexability, and we show that they hold for a wide range of problems of interest. Our key insight is to leverage the structure of the value function of individual robots, resulting in conditions that can be verified separately for each state of each robot. We apply these conditions to two types of transitions commonly seen in remote robot supervision systems. Through numerical simulations, we demonstrate the efficacy of Whittle index policy as a near-optimal and scalable approach that outperforms existing scalable methods.

Gambler's Ruin Bandit Problem

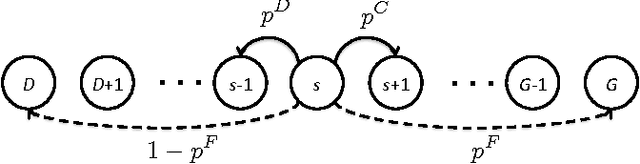
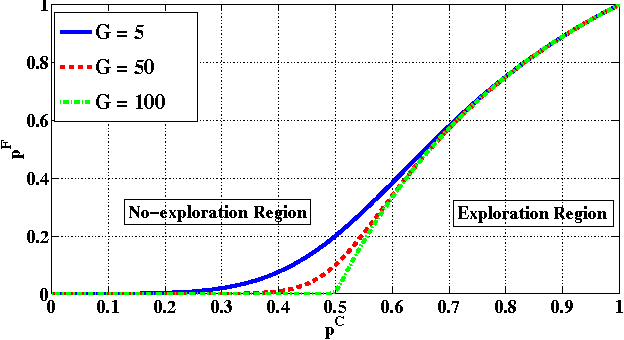
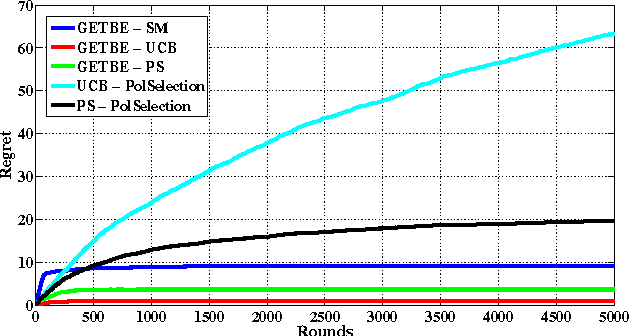
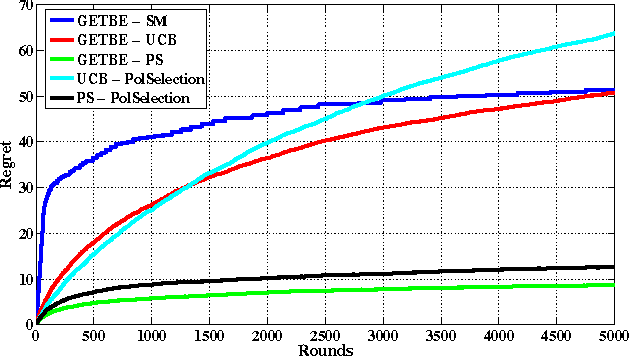
In this paper, we propose a new multi-armed bandit problem called the Gambler's Ruin Bandit Problem (GRBP). In the GRBP, the learner proceeds in a sequence of rounds, where each round is a Markov Decision Process (MDP) with two actions (arms): a continuation action that moves the learner randomly over the state space around the current state; and a terminal action that moves the learner directly into one of the two terminal states (goal and dead-end state). The current round ends when a terminal state is reached, and the learner incurs a positive reward only when the goal state is reached. The objective of the learner is to maximize its long-term reward (expected number of times the goal state is reached), without having any prior knowledge on the state transition probabilities. We first prove a result on the form of the optimal policy for the GRBP. Then, we define the regret of the learner with respect to an omnipotent oracle, which acts optimally in each round, and prove that it increases logarithmically over rounds. We also identify a condition under which the learner's regret is bounded. A potential application of the GRBP is optimal medical treatment assignment, in which the continuation action corresponds to a conservative treatment and the terminal action corresponds to a risky treatment such as surgery.