On learning history based policies for controlling Markov decision processes

Reinforcementlearning(RL)folkloresuggeststhathistory-basedfunctionapproximationmethods,suchas recurrent neural nets or history-based state abstraction, perform better than their memory-less counterparts, due to the fact that function approximation in Markov decision processes (MDP) can be viewed as inducing a Partially observable MDP. However, there has been little formal analysis of such history-based algorithms, as most existing frameworks focus exclusively on memory-less features. In this paper, we introduce a theoretical framework for studying the behaviour of RL algorithms that learn to control an MDP using history-based feature abstraction mappings. Furthermore, we use this framework to design a practical RL algorithm and we numerically evaluate its effectiveness on a set of continuous control tasks.

Finite time analysis of temporal difference learning with linear function approximation: Tail averaging and regularisation

We study the finite-time behaviour of the popular temporal difference (TD) learning algorithm when combined with tail-averaging. We derive finite time bounds on the parameter error of the tail-averaged TD iterate under a step-size choice that does not require information about the eigenvalues of the matrix underlying the projected TD fixed point. Our analysis shows that tail-averaged TD converges at the optimal $O\left(1/t\right)$ rate, both in expectation and with high probability. In addition, our bounds exhibit a sharper rate of decay for the initial error (bias), which is an improvement over averaging all iterates. We also propose and analyse a variant of TD that incorporates regularisation. From analysis, we conclude that the regularised version of TD is useful for problems with ill-conditioned features.

Variance Penalized On-Policy and Off-Policy Actor-Critic

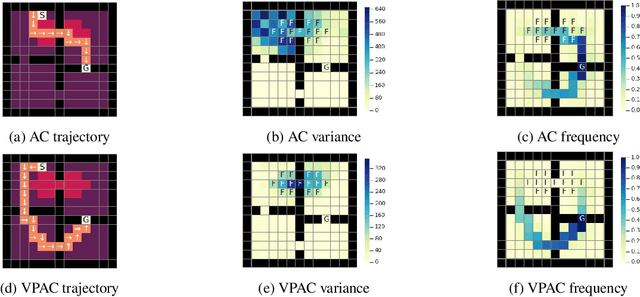
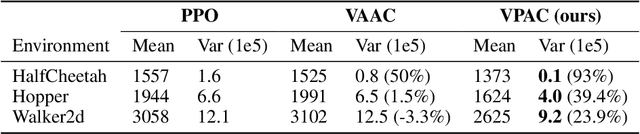
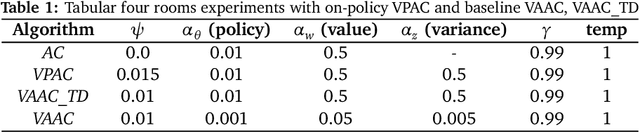
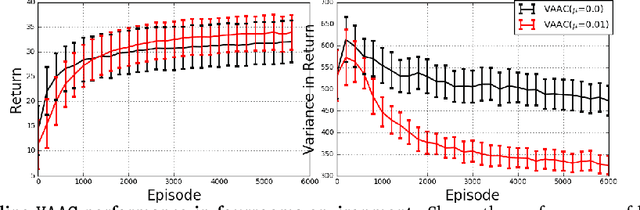
Reinforcement learning algorithms are typically geared towards optimizing the expected return of an agent. However, in many practical applications, low variance in the return is desired to ensure the reliability of an algorithm. In this paper, we propose on-policy and off-policy actor-critic algorithms that optimize a performance criterion involving both mean and variance in the return. Previous work uses the second moment of return to estimate the variance indirectly. Instead, we use a much simpler recently proposed direct variance estimator which updates the estimates incrementally using temporal difference methods. Using the variance-penalized criterion, we guarantee the convergence of our algorithm to locally optimal policies for finite state action Markov decision processes. We demonstrate the utility of our algorithm in tabular and continuous MuJoCo domains. Our approach not only performs on par with actor-critic and prior variance-penalization baselines in terms of expected return, but also generates trajectories which have lower variance in the return.