Concentration of Cumulative Reward in Markov Decision Processes

In this paper, we investigate the concentration properties of cumulative rewards in Markov Decision Processes (MDPs), focusing on both asymptotic and non-asymptotic settings. We introduce a unified approach to characterize reward concentration in MDPs, covering both infinite-horizon settings (i.e., average and discounted reward frameworks) and finite-horizon setting. Our asymptotic results include the law of large numbers, the central limit theorem, and the law of iterated logarithms, while our non-asymptotic bounds include Azuma-Hoeffding-type inequalities and a non-asymptotic version of the law of iterated logarithms. Additionally, we explore two key implications of our results. First, we analyze the sample path behavior of the difference in rewards between any two stationary policies. Second, we show that two alternative definitions of regret for learning policies proposed in the literature are rate-equivalent. Our proof techniques rely on a novel martingale decomposition of cumulative rewards, properties of the solution to the policy evaluation fixed-point equation, and both asymptotic and non-asymptotic concentration results for martingale difference sequences.

Transmission Neural Networks: From Virus Spread Models to Neural Networks

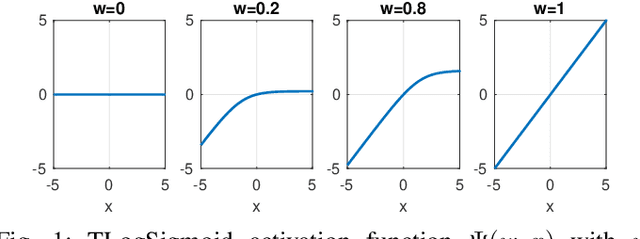
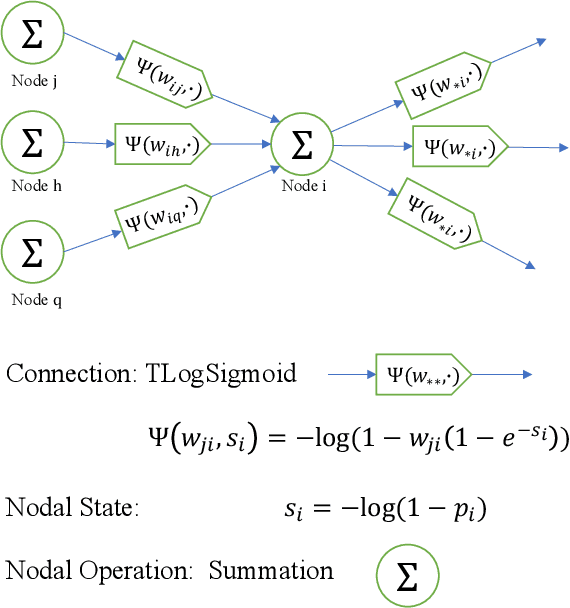
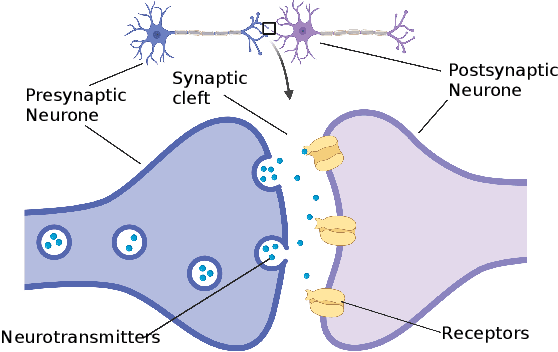
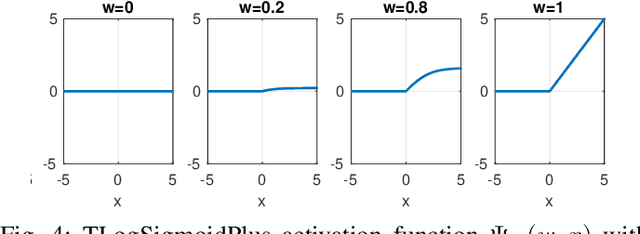
This work connects models for virus spread on networks with their equivalent neural network representations. Based on this connection, we propose a new neural network architecture, called Transmission Neural Networks (TransNNs) where activation functions are primarily associated with links and are allowed to have different activation levels. Furthermore, this connection leads to the discovery and the derivation of three new activation functions with tunable or trainable parameters. Moreover, we prove that TransNNs with a single hidden layer and a fixed non-zero bias term are universal function approximators. Finally, we present new fundamental derivations of continuous time epidemic network models based on TransNNs.

Consistency and Rate of Convergence of Switched Least Squares System Identification for Autonomous Switched Linear Systems

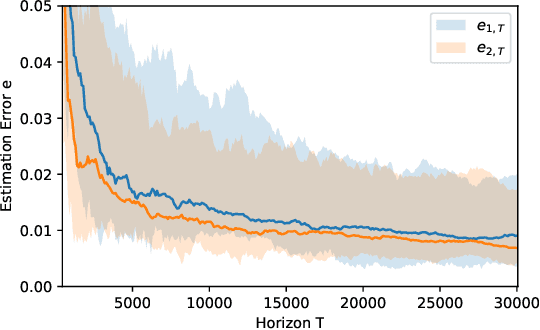
In this paper, we investigate the problem of system identification for autonomous switched linear systems with complete state observations. We propose switched least squares method for the identification for switched linear systems, show that this method is strongly consistent, and derive data-dependent and data-independent rates of convergence. In particular, our data-dependent rate of convergence shows that, almost surely, the system identification error is $\mathcal{O}\big(\sqrt{\log(T)/T} \big)$ where $T$ is the time horizon. These results show that our method for switched linear systems has the same rate of convergence as least squares method for non-switched linear systems. We compare our results with those in the literature. We present numerical examples to illustrate the performance of the proposed system identification method.