Markov Balance Satisfaction Improves Performance in Strictly Batch Offline Imitation Learning

Imitation learning (IL) is notably effective for robotic tasks where directly programming behaviors or defining optimal control costs is challenging. In this work, we address a scenario where the imitator relies solely on observed behavior and cannot make environmental interactions during learning. It does not have additional supplementary datasets beyond the expert's dataset nor any information about the transition dynamics. Unlike state-of-the-art (SOTA) IL methods, this approach tackles the limitations of conventional IL by operating in a more constrained and realistic setting. Our method uses the Markov balance equation and introduces a novel conditional density estimation-based imitation learning framework. It employs conditional normalizing flows for transition dynamics estimation and aims at satisfying a balance equation for the environment. Through a series of numerical experiments on Classic Control and MuJoCo environments, we demonstrate consistently superior empirical performance compared to many SOTA IL algorithms.

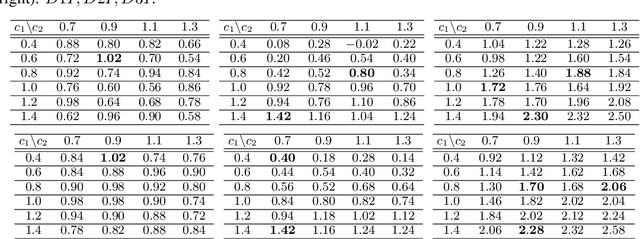
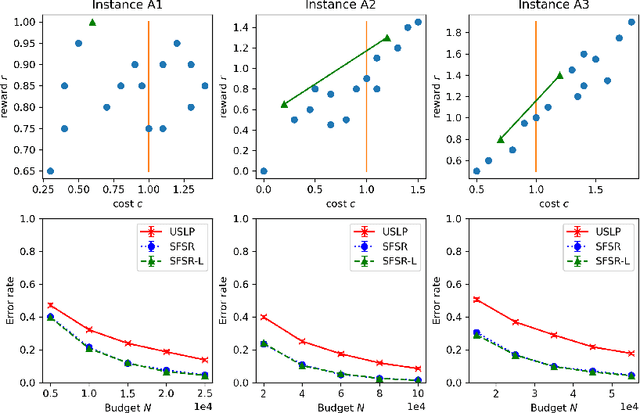
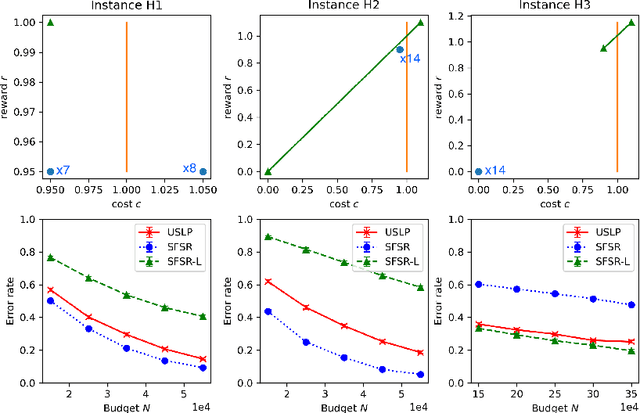
Pure Exploration for Constrained Best Mixed Arm Identification with a Fixed Budget

In this paper, we introduce the constrained best mixed arm identification (CBMAI) problem with a fixed budget. This is a pure exploration problem in a stochastic finite armed bandit model. Each arm is associated with a reward and multiple types of costs from unknown distributions. Unlike the unconstrained best arm identification problem, the optimal solution for the CBMAI problem may be a randomized mixture of multiple arms. The goal thus is to find the best mixed arm that maximizes the expected reward subject to constraints on the expected costs with a given learning budget $N$. We propose a novel, parameter-free algorithm, called the Score Function-based Successive Reject (SFSR) algorithm, that combines the classical successive reject framework with a novel score-function-based rejection criteria based on linear programming theory to identify the optimal support. We provide a theoretical upper bound on the mis-identification (of the the support of the best mixed arm) probability and show that it decays exponentially in the budget $N$ and some constants that characterize the hardness of the problem instance. We also develop an information theoretic lower bound on the error probability that shows that these constants appropriately characterize the problem difficulty. We validate this empirically on a number of average and hard instances.

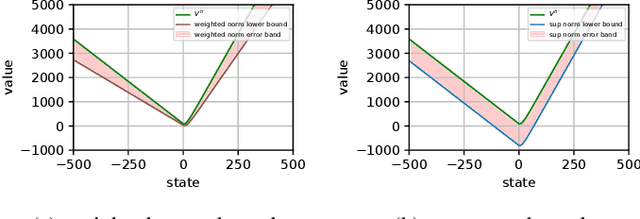
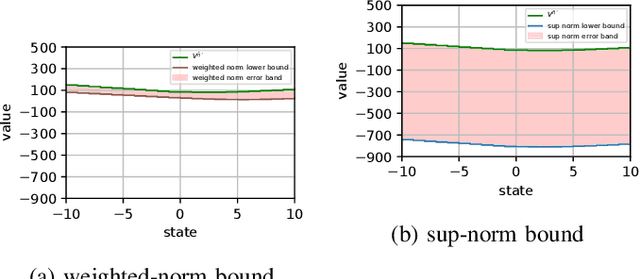
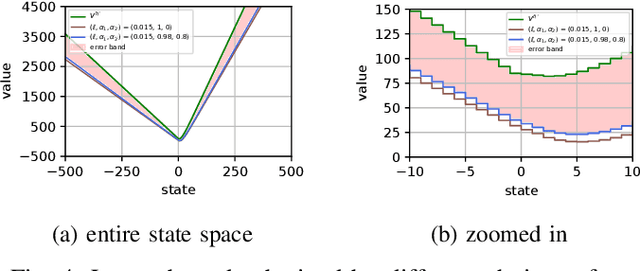
Model approximation in MDPs with unbounded per-step cost

We consider the problem of designing a control policy for an infinite-horizon discounted cost Markov decision process $\mathcal{M}$ when we only have access to an approximate model $\hat{\mathcal{M}}$. How well does an optimal policy $\hat{\pi}^{\star}$ of the approximate model perform when used in the original model $\mathcal{M}$? We answer this question by bounding a weighted norm of the difference between the value function of $\hat{\pi}^\star $ when used in $\mathcal{M}$ and the optimal value function of $\mathcal{M}$. We then extend our results and obtain potentially tighter upper bounds by considering affine transformations of the per-step cost. We further provide upper bounds that explicitly depend on the weighted distance between cost functions and weighted distance between transition kernels of the original and approximate models. We present examples to illustrate our results.

Regret Analysis of the Posterior Sampling-based Learning Algorithm for Episodic POMDPs

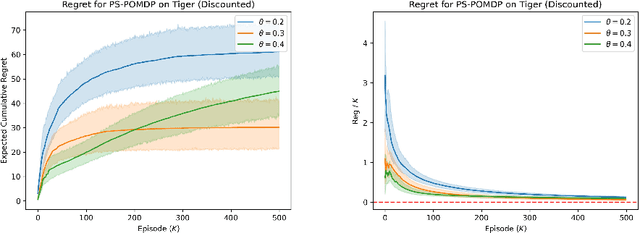
Compared to Markov Decision Processes (MDPs), learning in Partially Observable Markov Decision Processes (POMDPs) can be significantly harder due to the difficulty of interpreting observations. In this paper, we consider episodic learning problems in POMDPs with unknown transition and observation models. We consider the Posterior Sampling-based Reinforcement Learning (PSRL) algorithm for POMDPs and show that its Bayesian regret scales as the square root of the number of episodes. In general, the regret scales exponentially with the horizon length $H$, and we show that this is inevitable by providing a lower bound. However, under the condition that the POMDP is undercomplete and weakly revealing, we establish a polynomial Bayesian regret bound that improves the regret bound by a factor of $\Omega(H^2\sqrt{SA})$ over the recent result by arXiv:2204.08967.

Conditional Kernel Imitation Learning for Continuous State Environments

Imitation Learning (IL) is an important paradigm within the broader reinforcement learning (RL) methodology. Unlike most of RL, it does not assume availability of reward-feedback. Reward inference and shaping are known to be difficult and error-prone methods particularly when the demonstration data comes from human experts. Classical methods such as behavioral cloning and inverse reinforcement learning are highly sensitive to estimation errors, a problem that is particularly acute in continuous state space problems. Meanwhile, state-of-the-art IL algorithms convert behavioral policy learning problems into distribution-matching problems which often require additional online interaction data to be effective. In this paper, we consider the problem of imitation learning in continuous state space environments based solely on observed behavior, without access to transition dynamics information, reward structure, or, most importantly, any additional interactions with the environment. Our approach is based on the Markov balance equation and introduces a novel conditional kernel density estimation-based imitation learning framework. It involves estimating the environment's transition dynamics using conditional kernel density estimators and seeks to satisfy the probabilistic balance equations for the environment. We establish that our estimators satisfy basic asymptotic consistency requirements. Through a series of numerical experiments on continuous state benchmark environments, we show consistently superior empirical performance over many state-of-the-art IL algorithms.

Optimal Control of Logically Constrained Partially Observable and Multi-Agent Markov Decision Processes

Autonomous systems often have logical constraints arising, for example, from safety, operational, or regulatory requirements. Such constraints can be expressed using temporal logic specifications. The system state is often partially observable. Moreover, it could encompass a team of multiple agents with a common objective but disparate information structures and constraints. In this paper, we first introduce an optimal control theory for partially observable Markov decision processes (POMDPs) with finite linear temporal logic constraints. We provide a structured methodology for synthesizing policies that maximize a cumulative reward while ensuring that the probability of satisfying a temporal logic constraint is sufficiently high. Our approach comes with guarantees on approximate reward optimality and constraint satisfaction. We then build on this approach to design an optimal control framework for logically constrained multi-agent settings with information asymmetry. We illustrate the effectiveness of our approach by implementing it on several case studies.

A Novel Point-based Algorithm for Multi-agent Control Using the Common Information Approach

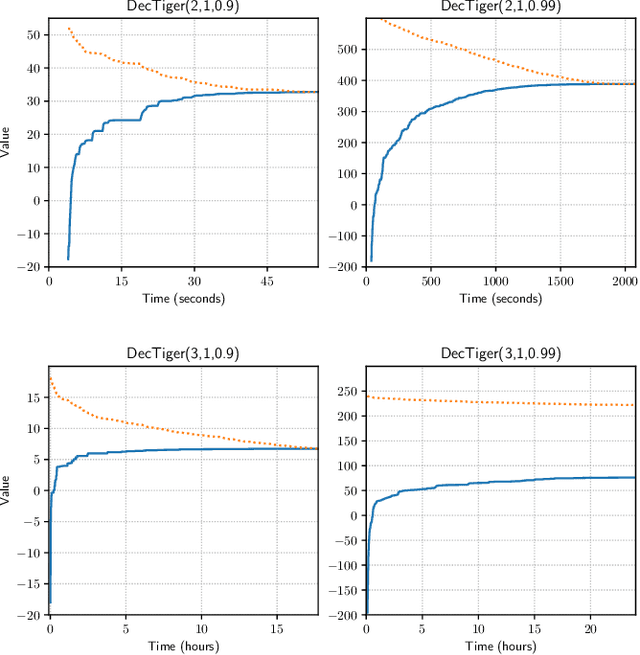
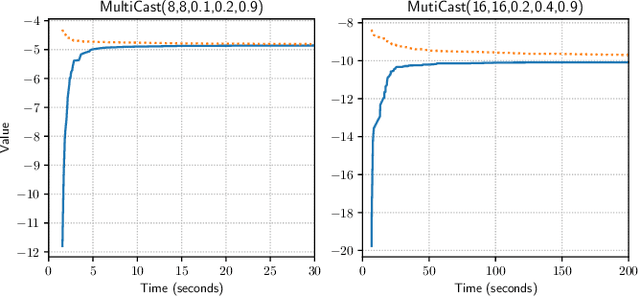
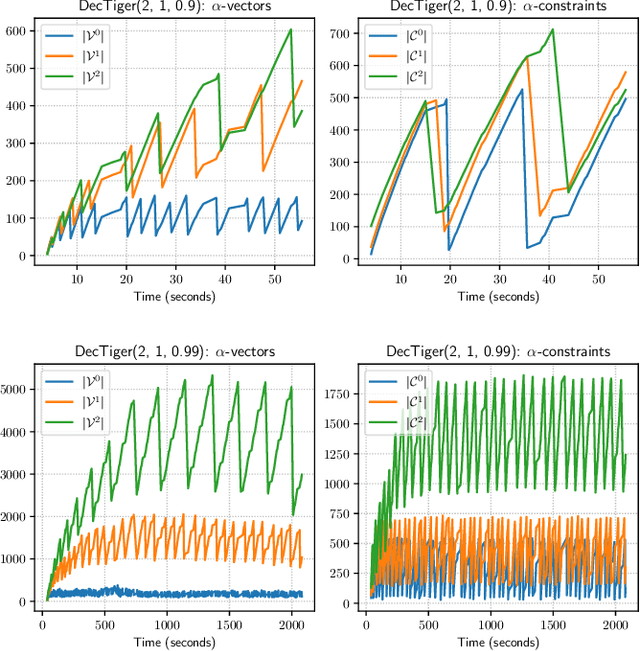
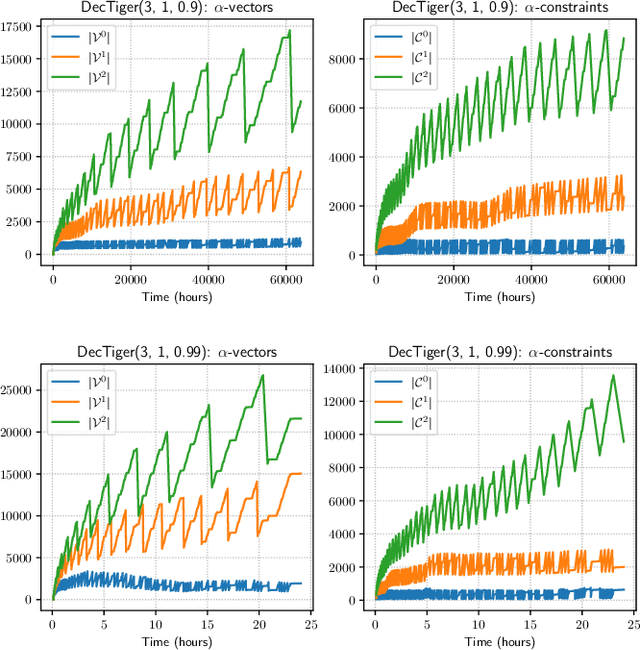
The Common Information (CI) approach provides a systematic way to transform a multi-agent stochastic control problem to a single-agent partially observed Markov decision problem (POMDP) called the coordinator's POMDP. However, such a POMDP can be hard to solve due to its extraordinarily large action space. We propose a new algorithm for multi-agent stochastic control problems, called coordinator's heuristic search value iteration (CHSVI), that combines the CI approach and point-based POMDP algorithms for large action spaces. We demonstrate the algorithm through optimally solving several benchmark problems.

Learning Zero-sum Stochastic Games with Posterior Sampling

In this paper, we propose Posterior Sampling Reinforcement Learning for Zero-sum Stochastic Games (PSRL-ZSG), the first online learning algorithm that achieves Bayesian regret bound of $O(HS\sqrt{AT})$ in the infinite-horizon zero-sum stochastic games with average-reward criterion. Here $H$ is an upper bound on the span of the bias function, $S$ is the number of states, $A$ is the number of joint actions and $T$ is the horizon. We consider the online setting where the opponent can not be controlled and can take any arbitrary time-adaptive history-dependent strategy. This improves the best existing regret bound of $O(\sqrt[3]{DS^2AT^2})$ by Wei et. al., 2017 under the same assumption and matches the theoretical lower bound in $A$ and $T$.

A relaxed technical assumption for posterior sampling-based reinforcement learning for control of unknown linear systems

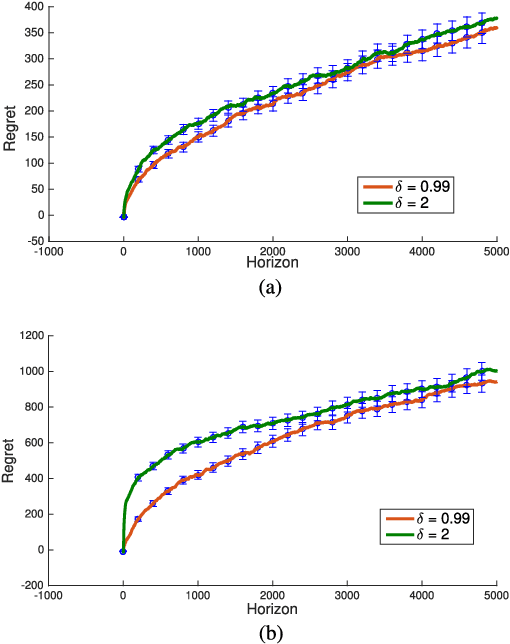
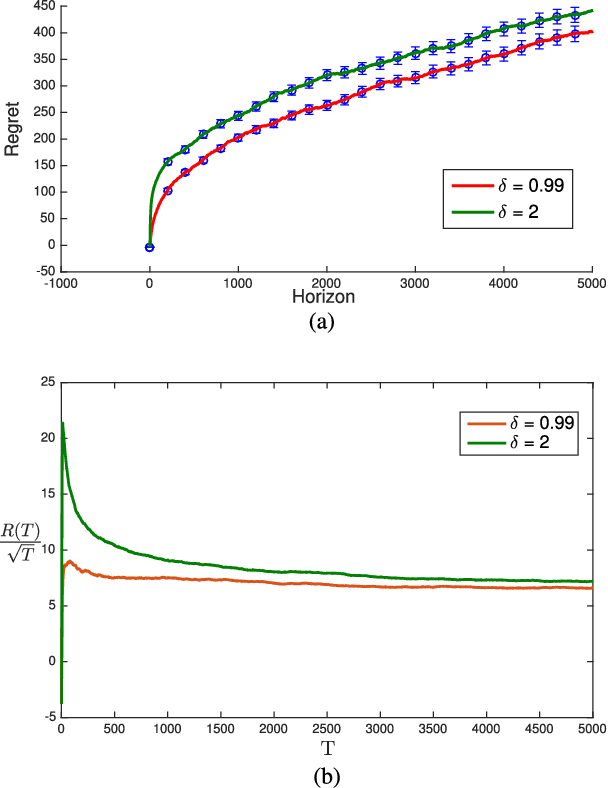
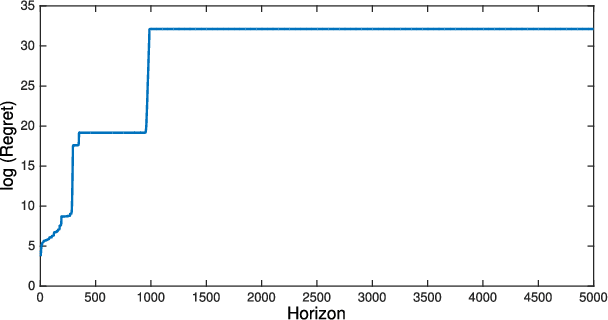
We revisit the Thompson sampling algorithm to control an unknown linear quadratic (LQ) system recently proposed by Ouyang et al (arXiv:1709.04047). The regret bound of the algorithm was derived under a technical assumption on the induced norm of the closed loop system. In this technical note, we show that by making a minor modification in the algorithm (in particular, ensuring that an episode does not end too soon), this technical assumption on the induced norm can be replaced by a milder assumption in terms of the spectral radius of the closed loop system. The modified algorithm has the same Bayesian regret of $\tilde{\mathcal{O}}(\sqrt{T})$, where $T$ is the time-horizon and the $\tilde{\mathcal{O}}(\cdot)$ notation hides logarithmic terms in~$T$.

Scalable regret for learning to control network-coupled subsystems with unknown dynamics

We consider the problem of controlling an unknown linear quadratic Gaussian (LQG) system consisting of multiple subsystems connected over a network. Our goal is to minimize and quantify the regret (i.e. loss in performance) of our strategy with respect to an oracle who knows the system model. Viewing the interconnected subsystems globally and directly using existing LQG learning algorithms for the global system results in a regret that increases super-linearly with the number of subsystems. Instead, we propose a new Thompson sampling based learning algorithm which exploits the structure of the underlying network. We show that the expected regret of the proposed algorithm is bounded by $\tilde{\mathcal{O}} \big( n \sqrt{T} \big)$ where $n$ is the number of subsystems, $T$ is the time horizon and the $\tilde{\mathcal{O}}(\cdot)$ notation hides logarithmic terms in $n$ and $T$. Thus, the regret scales linearly with the number of subsystems. We present numerical experiments to illustrate the salient features of the proposed algorithm.