A relaxed technical assumption for posterior sampling-based reinforcement learning for control of unknown linear systems
Paper and Code
Aug 19, 2021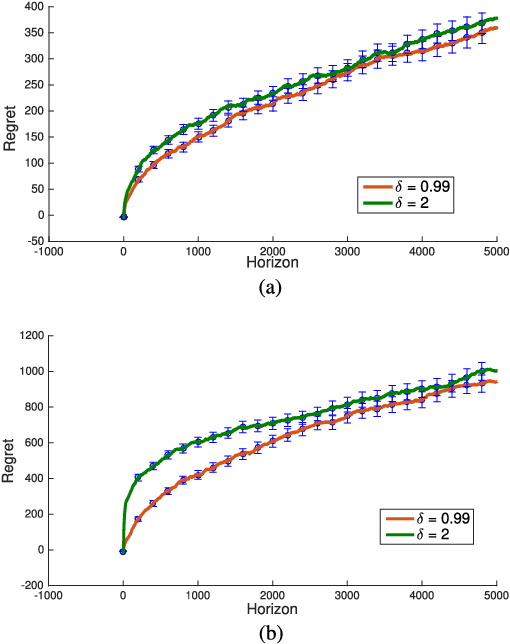
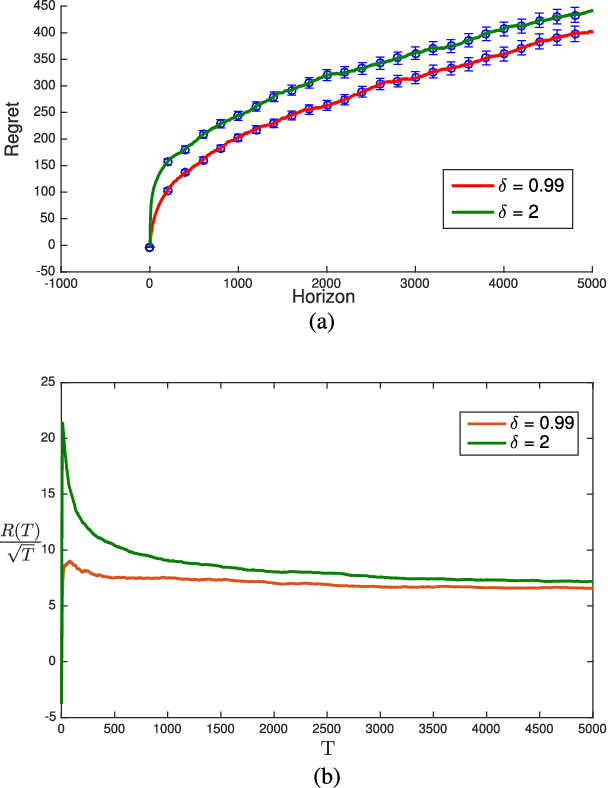
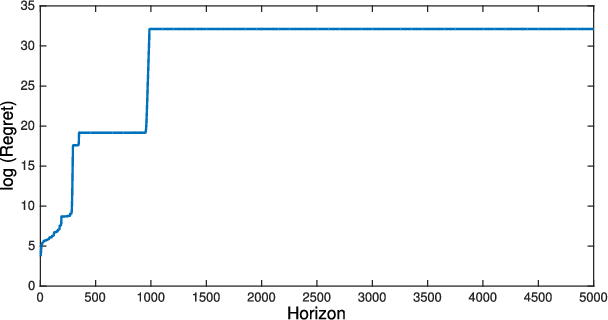
We revisit the Thompson sampling algorithm to control an unknown linear quadratic (LQ) system recently proposed by Ouyang et al (arXiv:1709.04047). The regret bound of the algorithm was derived under a technical assumption on the induced norm of the closed loop system. In this technical note, we show that by making a minor modification in the algorithm (in particular, ensuring that an episode does not end too soon), this technical assumption on the induced norm can be replaced by a milder assumption in terms of the spectral radius of the closed loop system. The modified algorithm has the same Bayesian regret of $\tilde{\mathcal{O}}(\sqrt{T})$, where $T$ is the time-horizon and the $\tilde{\mathcal{O}}(\cdot)$ notation hides logarithmic terms in~$T$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge