A relaxed technical assumption for posterior sampling-based reinforcement learning for control of unknown linear systems

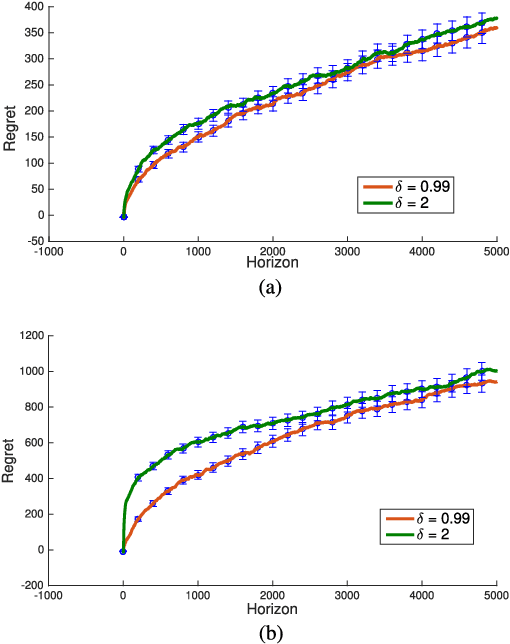
We revisit the Thompson sampling algorithm to control an unknown linear quadratic (LQ) system recently proposed by Ouyang et al (arXiv:1709.04047). The regret bound of the algorithm was derived under a technical assumption on the induced norm of the closed loop system. In this technical note, we show that by making a minor modification in the algorithm (in particular, ensuring that an episode does not end too soon), this technical assumption on the induced norm can be replaced by a milder assumption in terms of the spectral radius of the closed loop system. The modified algorithm has the same Bayesian regret of $\tilde{\mathcal{O}}(\sqrt{T})$, where $T$ is the time-horizon and the $\tilde{\mathcal{O}}(\cdot)$ notation hides logarithmic terms in~$T$.

Scalable regret for learning to control network-coupled subsystems with unknown dynamics

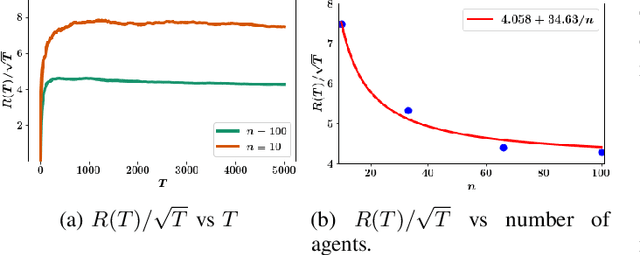
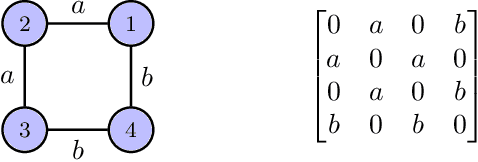
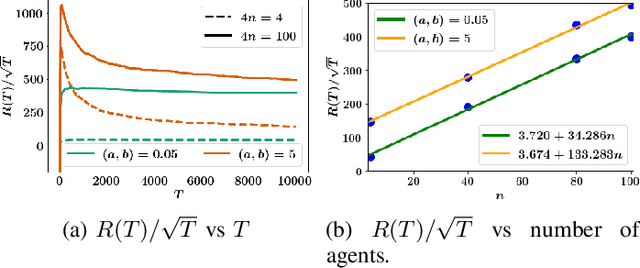
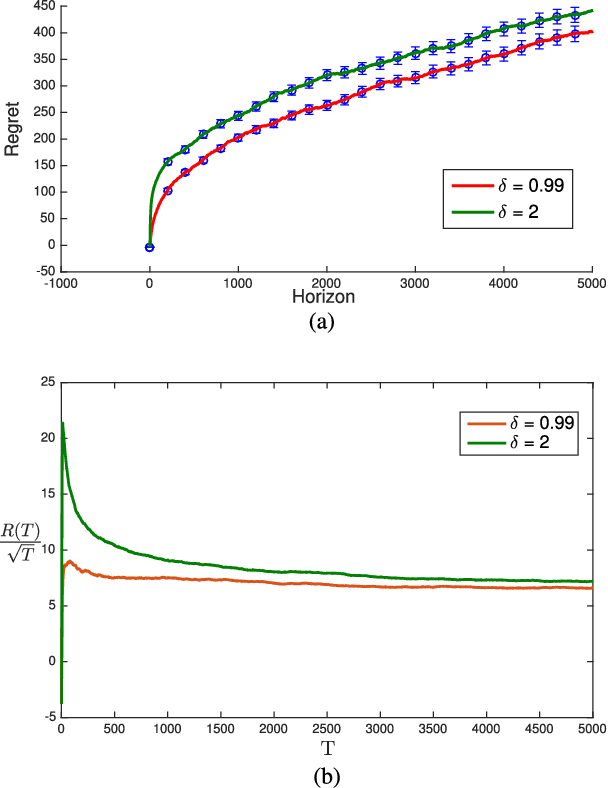
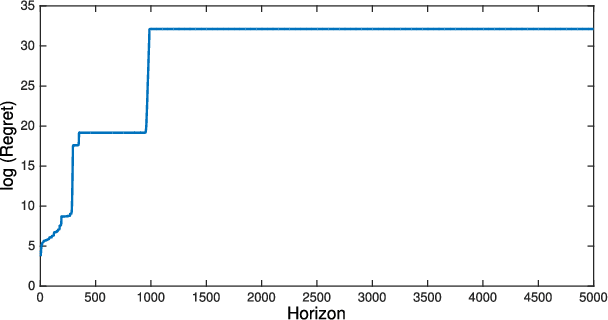
We consider the problem of controlling an unknown linear quadratic Gaussian (LQG) system consisting of multiple subsystems connected over a network. Our goal is to minimize and quantify the regret (i.e. loss in performance) of our strategy with respect to an oracle who knows the system model. Viewing the interconnected subsystems globally and directly using existing LQG learning algorithms for the global system results in a regret that increases super-linearly with the number of subsystems. Instead, we propose a new Thompson sampling based learning algorithm which exploits the structure of the underlying network. We show that the expected regret of the proposed algorithm is bounded by $\tilde{\mathcal{O}} \big( n \sqrt{T} \big)$ where $n$ is the number of subsystems, $T$ is the time horizon and the $\tilde{\mathcal{O}}(\cdot)$ notation hides logarithmic terms in $n$ and $T$. Thus, the regret scales linearly with the number of subsystems. We present numerical experiments to illustrate the salient features of the proposed algorithm.

Thompson sampling for linear quadratic mean-field teams

We consider optimal control of an unknown multi-agent linear quadratic (LQ) system where the dynamics and the cost are coupled across the agents through the mean-field (i.e., empirical mean) of the states and controls. Directly using single-agent LQ learning algorithms in such models results in regret which increases polynomially with the number of agents. We propose a new Thompson sampling based learning algorithm which exploits the structure of the system model and show that the expected Bayesian regret of our proposed algorithm for a system with agents of $|M|$ different types at time horizon $T$ is $\tilde{\mathcal{O}} \big( |M|^{1.5} \sqrt{T} \big)$ irrespective of the total number of agents, where the $\tilde{\mathcal{O}}$ notation hides logarithmic factors in $T$. We present detailed numerical experiments to illustrate the salient features of the proposed algorithm.