Regret Analysis of the Posterior Sampling-based Learning Algorithm for Episodic POMDPs

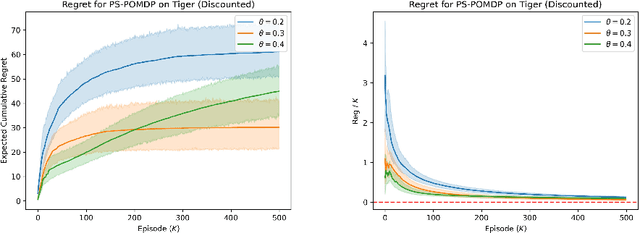
Compared to Markov Decision Processes (MDPs), learning in Partially Observable Markov Decision Processes (POMDPs) can be significantly harder due to the difficulty of interpreting observations. In this paper, we consider episodic learning problems in POMDPs with unknown transition and observation models. We consider the Posterior Sampling-based Reinforcement Learning (PSRL) algorithm for POMDPs and show that its Bayesian regret scales as the square root of the number of episodes. In general, the regret scales exponentially with the horizon length $H$, and we show that this is inevitable by providing a lower bound. However, under the condition that the POMDP is undercomplete and weakly revealing, we establish a polynomial Bayesian regret bound that improves the regret bound by a factor of $\Omega(H^2\sqrt{SA})$ over the recent result by arXiv:2204.08967.