Model approximation in MDPs with unbounded per-step cost
Paper and Code
Feb 13, 2024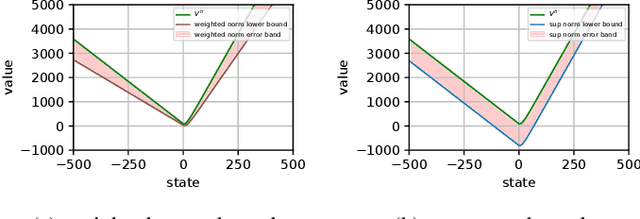
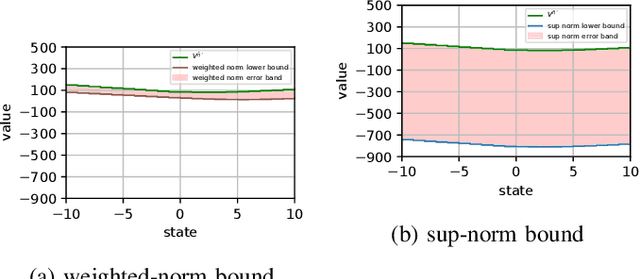

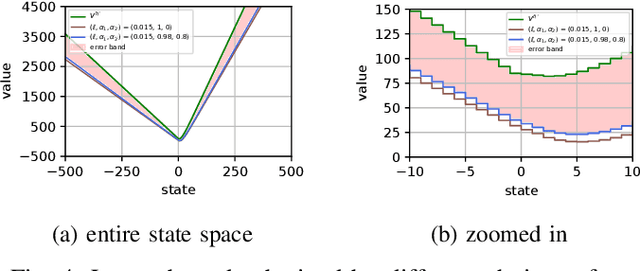
We consider the problem of designing a control policy for an infinite-horizon discounted cost Markov decision process $\mathcal{M}$ when we only have access to an approximate model $\hat{\mathcal{M}}$. How well does an optimal policy $\hat{\pi}^{\star}$ of the approximate model perform when used in the original model $\mathcal{M}$? We answer this question by bounding a weighted norm of the difference between the value function of $\hat{\pi}^\star $ when used in $\mathcal{M}$ and the optimal value function of $\mathcal{M}$. We then extend our results and obtain potentially tighter upper bounds by considering affine transformations of the per-step cost. We further provide upper bounds that explicitly depend on the weighted distance between cost functions and weighted distance between transition kernels of the original and approximate models. We present examples to illustrate our results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge