Mehdi Jafarnia-Jahromi
Learning Zero-sum Stochastic Games with Posterior Sampling
Sep 08, 2021Abstract:In this paper, we propose Posterior Sampling Reinforcement Learning for Zero-sum Stochastic Games (PSRL-ZSG), the first online learning algorithm that achieves Bayesian regret bound of $O(HS\sqrt{AT})$ in the infinite-horizon zero-sum stochastic games with average-reward criterion. Here $H$ is an upper bound on the span of the bias function, $S$ is the number of states, $A$ is the number of joint actions and $T$ is the horizon. We consider the online setting where the opponent can not be controlled and can take any arbitrary time-adaptive history-dependent strategy. This improves the best existing regret bound of $O(\sqrt[3]{DS^2AT^2})$ by Wei et. al., 2017 under the same assumption and matches the theoretical lower bound in $A$ and $T$.
Online Learning for Cooperative Multi-Player Multi-Armed Bandits
Sep 07, 2021
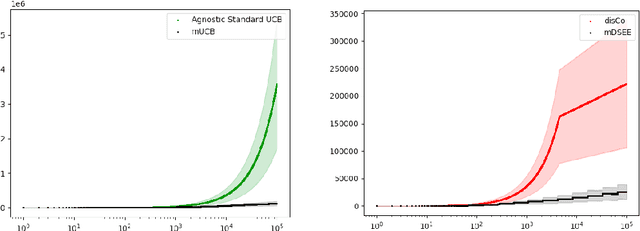
Abstract:We introduce a framework for decentralized online learning for multi-armed bandits (MAB) with multiple cooperative players. The reward obtained by the players in each round depends on the actions taken by all the players. It's a team setting, and the objective is common. Information asymmetry is what makes the problem interesting and challenging. We consider three types of information asymmetry: action information asymmetry when the actions of the players can't be observed but the rewards received are common; reward information asymmetry when the actions of the other players are observable but rewards received are IID from the same distribution; and when we have both action and reward information asymmetry. For the first setting, we propose a UCB-inspired algorithm that achieves $O(\log T)$ regret whether the rewards are IID or Markovian. For the second section, we offer an environment such that the algorithm given for the first setting gives linear regret. For the third setting, we show that a variation of the `explore then commit' algorithm achieves almost log regret.
Implicit Finite-Horizon Approximation and Efficient Optimal Algorithms for Stochastic Shortest Path
Jun 15, 2021



Abstract:We introduce a generic template for developing regret minimization algorithms in the Stochastic Shortest Path (SSP) model, which achieves minimax optimal regret as long as certain properties are ensured. The key of our analysis is a new technique called implicit finite-horizon approximation, which approximates the SSP model by a finite-horizon counterpart only in the analysis without explicit implementation. Using this template, we develop two new algorithms: the first one is model-free (the first in the literature to our knowledge) and minimax optimal under strictly positive costs; the second one is model-based and minimax optimal even with zero-cost state-action pairs, matching the best existing result from [Tarbouriech et al., 2021b]. Importantly, both algorithms admit highly sparse updates, making them computationally more efficient than all existing algorithms. Moreover, both can be made completely parameter-free.
Online Learning for Stochastic Shortest Path Model via Posterior Sampling
Jun 09, 2021
Abstract:We consider the problem of online reinforcement learning for the Stochastic Shortest Path (SSP) problem modeled as an unknown MDP with an absorbing state. We propose PSRL-SSP, a simple posterior sampling-based reinforcement learning algorithm for the SSP problem. The algorithm operates in epochs. At the beginning of each epoch, a sample is drawn from the posterior distribution on the unknown model dynamics, and the optimal policy with respect to the drawn sample is followed during that epoch. An epoch completes if either the number of visits to the goal state in the current epoch exceeds that of the previous epoch, or the number of visits to any of the state-action pairs is doubled. We establish a Bayesian regret bound of $O(B_\star S\sqrt{AK})$, where $B_\star$ is an upper bound on the expected cost of the optimal policy, $S$ is the size of the state space, $A$ is the size of the action space, and $K$ is the number of episodes. The algorithm only requires the knowledge of the prior distribution, and has no hyper-parameters to tune. It is the first such posterior sampling algorithm and outperforms numerically previously proposed optimism-based algorithms.
Online Learning for Unknown Partially Observable MDPs
Feb 25, 2021Abstract:Solving Partially Observable Markov Decision Processes (POMDPs) is hard. Learning optimal controllers for POMDPs when the model is unknown is harder. Online learning of optimal controllers for unknown POMDPs, which requires efficient learning using regret-minimizing algorithms that effectively tradeoff exploration and exploitation, is even harder, and no solution exists currently. In this paper, we consider infinite-horizon average-cost POMDPs with unknown transition model, though known observation model. We propose a natural posterior sampling-based reinforcement learning algorithm (POMDP-PSRL) and show that it achieves $O(T^{2/3})$ regret where $T$ is the time horizon. To the best of our knowledge, this is the first online RL algorithm for POMDPs and has sub-linear regret.
Learning Infinite-horizon Average-reward MDPs with Linear Function Approximation
Jul 23, 2020
Abstract:We develop several new algorithms for learning Markov Decision Processes in an infinite-horizon average-reward setting with linear function approximation. Using the optimism principle and assuming that the MDP has a linear structure, we first propose a computationally inefficient algorithm with optimal $\widetilde{O}(\sqrt{T})$ regret and another computationally efficient variant with $\widetilde{O}(T^{3/4})$ regret, where $T$ is the number of interactions. Next, taking inspiration from adversarial linear bandits, we develop yet another efficient algorithm with $\widetilde{O}(\sqrt{T})$ regret under a different set of assumptions, improving the best existing result by Hao et al. (2020) with $\widetilde{O}(T^{2/3})$ regret. Moreover, we draw a connection between this algorithm and the Natural Policy Gradient algorithm proposed by Kakade (2002), and show that our analysis improves the sample complexity bound recently given by Agarwal et al. (2020).
A Model-free Learning Algorithm for Infinite-horizon Average-reward MDPs with Near-optimal Regret
Jun 08, 2020


Abstract:Recently, model-free reinforcement learning has attracted research attention due to its simplicity, memory and computation efficiency, and the flexibility to combine with function approximation. In this paper, we propose Exploration Enhanced Q-learning (EE-QL), a model-free algorithm for infinite-horizon average-reward Markov Decision Processes (MDPs) that achieves regret bound of $O(\sqrt{T})$ for the general class of weakly communicating MDPs, where $T$ is the number of interactions. EE-QL assumes that an online concentrating approximation of the optimal average reward is available. This is the first model-free learning algorithm that achieves $O(\sqrt T)$ regret without the ergodic assumption, and matches the lower bound in terms of $T$ except for logarithmic factors. Experiments show that the proposed algorithm performs as well as the best known model-based algorithms.
Model-free Reinforcement Learning in Infinite-horizon Average-reward Markov Decision Processes
Oct 15, 2019

Abstract:Model-free reinforcement learning is known to be memory and computation efficient and more amendable to large scale problems. In this paper, two model-free algorithms are introduced for learning infinite-horizon average-reward Markov Decision Processes (MDPs). The first algorithm reduces the problem to the discounted-reward version and achieves $\mathcal{O}(T^{2/3})$ regret after $T$ steps, under the minimal assumption of weakly communicating MDPs. The second algorithm makes use of recent advances in adaptive algorithms for adversarial multi-armed bandits and improves the regret to $\mathcal{O}(\sqrt{T})$, albeit with a stronger ergodic assumption. To the best of our knowledge, these are the first model-free algorithms with sub-linear regret (that is polynomial in all parameters) in the infinite-horizon average-reward setting.
PPD: Permutation Phase Defense Against Adversarial Examples in Deep Learning
Dec 25, 2018


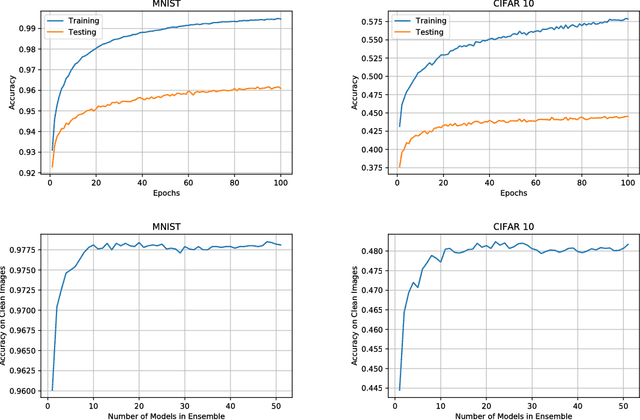
Abstract:Deep neural networks have demonstrated cutting edge performance on various tasks including classification. However, it is well known that adversarially designed imperceptible perturbation of the input can mislead advanced classifiers. In this paper, Permutation Phase Defense (PPD), is proposed as a novel method to resist adversarial attacks. PPD combines random permutation of the image with phase component of its Fourier transform. The basic idea behind this approach is to turn adversarial defense problems analogously into symmetric cryptography, which relies solely on safekeeping of the keys for security. In PPD, safe keeping of the selected permutation ensures effectiveness against adversarial attacks. Testing PPD on MNIST and CIFAR-10 datasets yielded state-of-the-art robustness against the most powerful adversarial attacks currently available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge