Online Learning for Cooperative Multi-Player Multi-Armed Bandits
Paper and Code
Sep 07, 2021
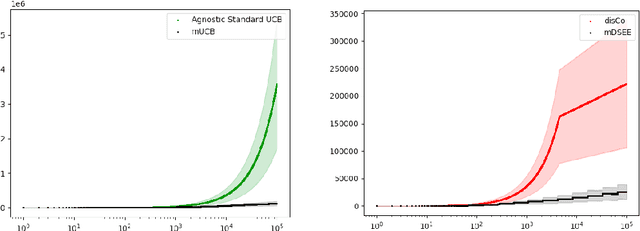
We introduce a framework for decentralized online learning for multi-armed bandits (MAB) with multiple cooperative players. The reward obtained by the players in each round depends on the actions taken by all the players. It's a team setting, and the objective is common. Information asymmetry is what makes the problem interesting and challenging. We consider three types of information asymmetry: action information asymmetry when the actions of the players can't be observed but the rewards received are common; reward information asymmetry when the actions of the other players are observable but rewards received are IID from the same distribution; and when we have both action and reward information asymmetry. For the first setting, we propose a UCB-inspired algorithm that achieves $O(\log T)$ regret whether the rewards are IID or Markovian. For the second section, we offer an environment such that the algorithm given for the first setting gives linear regret. For the third setting, we show that a variation of the `explore then commit' algorithm achieves almost log regret.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge