How Is Uncertainty Propagated in Knowledge Distillation?

Knowledge distillation transfers behavior from a teacher to a student model, but the process is inherently stochastic: teacher outputs, student training, and student inference can all be random. Collapsing these uncertainties to a single point estimate can distort what is learned. We systematically study how uncertainty propagates through knowledge distillation across three representative model classes--linear regression, feed-forward neural networks, and large language models (LLMs)--and propose simple corrections. We distinguish inter-student uncertainty (variance across independently distilled students) from intra-student uncertainty (variance of a single student's predictive distribution), showing that standard single-response knowledge distillation suppresses intra-student variance while leaving substantial inter-student variability. To address these mismatches, we introduce two variance-aware strategies: averaging multiple teacher responses, which reduces noise at rate $O(1/k)$, and variance-weighting, which combines teacher and student estimates via inverse-variance weighting to yield a minimum-variance estimator. We provide formal guarantees in linear regression, validate the methods in neural networks, and demonstrate empirical gains in LLM distillation, including reduced systematic noise and hallucination. These results reframe knowledge distillation as an uncertainty transformation and show that variance-aware distillation produces more stable students that better reflect teacher uncertainty.

Spectral Geometry for Deep Learning: Compression and Hallucination Detection via Random Matrix Theory

Large language models and deep neural networks achieve strong performance but suffer from reliability issues and high computational cost. This thesis proposes a unified framework based on spectral geometry and random matrix theory to address both problems by analyzing the eigenvalue structure of hidden activations. The first contribution, EigenTrack, is a real-time method for detecting hallucinations and out-of-distribution behavior in language and vision-language models using spectral features and their temporal dynamics. The second contribution, RMT-KD, is a principled compression method that identifies informative spectral components and applies iterative knowledge distillation to produce compact and efficient models while preserving accuracy. Together, these results show that spectral statistics provide interpretable and robust signals for monitoring uncertainty and guiding compression in large-scale neural networks.

SPARK: Igniting Communication-Efficient Decentralized Learning via Stage-wise Projected NTK and Accelerated Regularization

Decentralized federated learning (DFL) faces critical challenges from statistical heterogeneity and communication overhead. While NTK-based methods achieve faster convergence, transmitting full Jacobian matrices is impractical for bandwidth-constrained edge networks. We propose SPARK, synergistically integrating random projection-based Jacobian compression, stage-wise annealed distillation, and Nesterov momentum acceleration. Random projections compress Jacobians while preserving spectral properties essential for convergence. Stage-wise annealed distillation transitions from pure NTK evolution to neighbor-regularized learning, counteracting compression noise. Nesterov momentum accelerates convergence through stable accumulation enabled by distillation smoothing. SPARK achieves 98.7% communication reduction compared to NTK-DFL while maintaining convergence speed and superior accuracy. With momentum, SPARK reaches target performance 3 times faster, establishing state-of-the-art results for communication-efficient decentralized learning and enabling practical deployment in bandwidth-limited edge environments.

FSC-Net: Fast-Slow Consolidation Networks for Continual Learning

Continual learning remains challenging due to catastrophic forgetting, where neural networks lose previously acquired knowledge when learning new tasks. Inspired by memory consolidation in neuroscience, we propose FSC-Net (Fast-Slow Consolidation Networks), a dual-network architecture that separates rapid task learning from gradual knowledge consolidation. Our method employs a fast network (NN1) for immediate adaptation to new tasks and a slow network (NN2) that consolidates knowledge through distillation and replay. Within the family of MLP-based NN1 variants we evaluated, consolidation effectiveness is driven more by methodology than architectural embellishments -- a simple MLP outperforms more complex similarity-gated variants by 1.2pp. Through systematic hyperparameter analysis, we observed empirically that pure replay without distillation during consolidation achieves superior performance, consistent with the hypothesis that distillation from the fast network introduces recency bias. On Split-MNIST (30 seeds), FSC-Net achieves 91.71% +/- 0.62% retention accuracy, a +4.27pp gain over the fast network alone (87.43% +/- 1.27%, paired t=23.585, p < 1e-10). On Split-CIFAR-10 (5 seeds), our method achieves 33.31% +/- 0.38% retention with an +8.20pp gain over the fast network alone (25.11% +/- 1.61%, paired t=9.75, p < 1e-3), demonstrating +8.20pp gain, though absolute performance (33.31%) remains modest and below random expectation, highlighting need for stronger backbones. Our results provide empirical evidence that the dual-timescale consolidation mechanism, rather than architectural complexity, is central to mitigating catastrophic forgetting in this setting.

Towards Reliable LLM-based Robot Planning via Combined Uncertainty Estimation

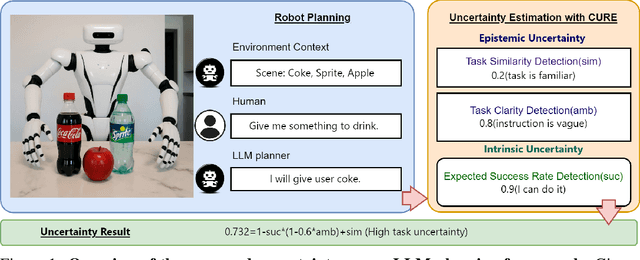
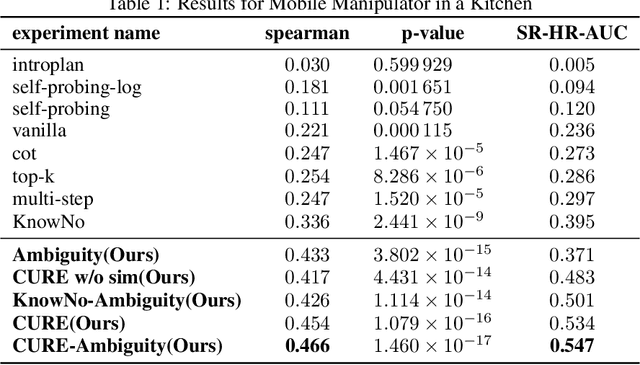
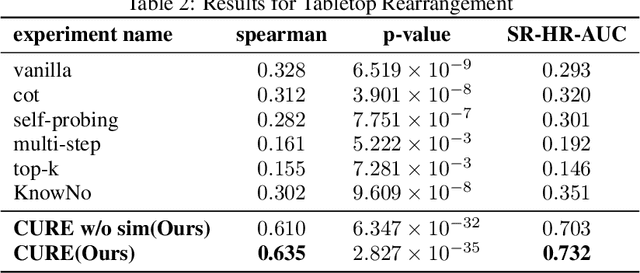
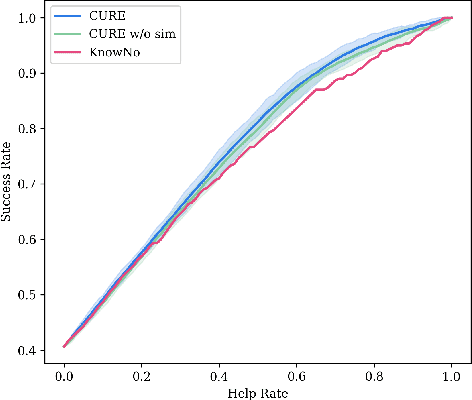
Large language models (LLMs) demonstrate advanced reasoning abilities, enabling robots to understand natural language instructions and generate high-level plans with appropriate grounding. However, LLM hallucinations present a significant challenge, often leading to overconfident yet potentially misaligned or unsafe plans. While researchers have explored uncertainty estimation to improve the reliability of LLM-based planning, existing studies have not sufficiently differentiated between epistemic and intrinsic uncertainty, limiting the effectiveness of uncertainty esti- mation. In this paper, we present Combined Uncertainty estimation for Reliable Embodied planning (CURE), which decomposes the uncertainty into epistemic and intrinsic uncertainty, each estimated separately. Furthermore, epistemic uncertainty is subdivided into task clarity and task familiarity for more accurate evaluation. The overall uncertainty assessments are obtained using random network distillation and multi-layer perceptron regression heads driven by LLM features. We validated our approach in two distinct experimental settings: kitchen manipulation and tabletop rearrangement experiments. The results show that, compared to existing methods, our approach yields uncertainty estimates that are more closely aligned with the actual execution outcomes.

Failure Prediction at Runtime for Generative Robot Policies

Imitation learning (IL) with generative models, such as diffusion and flow matching, has enabled robots to perform complex, long-horizon tasks. However, distribution shifts from unseen environments or compounding action errors can still cause unpredictable and unsafe behavior, leading to task failure. Early failure prediction during runtime is therefore essential for deploying robots in human-centered and safety-critical environments. We propose FIPER, a general framework for Failure Prediction at Runtime for generative IL policies that does not require failure data. FIPER identifies two key indicators of impending failure: (i) out-of-distribution (OOD) observations detected via random network distillation in the policy's embedding space, and (ii) high uncertainty in generated actions measured by a novel action-chunk entropy score. Both failure prediction scores are calibrated using a small set of successful rollouts via conformal prediction. A failure alarm is triggered when both indicators, aggregated over short time windows, exceed their thresholds. We evaluate FIPER across five simulation and real-world environments involving diverse failure modes. Our results demonstrate that FIPER better distinguishes actual failures from benign OOD situations and predicts failures more accurately and earlier than existing methods. We thus consider this work an important step towards more interpretable and safer generative robot policies. Code, data and videos are available at https://tum-lsy.github.io/fiper_website.

Where to Begin: Efficient Pretraining via Subnetwork Selection and Distillation

Small Language models (SLMs) offer an efficient and accessible alternative to Large Language Models (LLMs), delivering strong performance while using far fewer resources. We introduce a simple and effective framework for pretraining SLMs that brings together three complementary ideas. First, we identify structurally sparse sub-network initializations that consistently outperform randomly initialized models of similar size under the same compute budget. Second, we use evolutionary search to automatically discover high-quality sub-network initializations, providing better starting points for pretraining. Third, we apply knowledge distillation from larger teacher models to speed up training and improve generalization. Together, these components make SLM pretraining substantially more efficient: our best model, discovered using evolutionary search and initialized with LLM weights, matches the validation perplexity of a comparable Pythia SLM while requiring 9.2x fewer pretraining tokens. We release all code and models at https://github.com/whittle-org/whittle/, offering a practical and reproducible path toward cost-efficient small language model development at scale.

Beyond Random: Automatic Inner-loop Optimization in Dataset Distillation

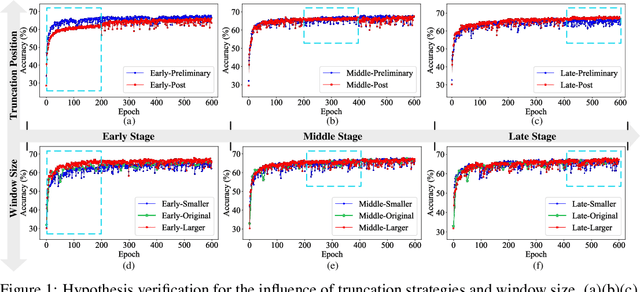
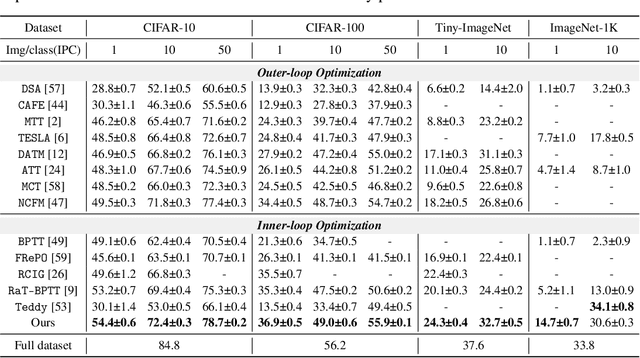
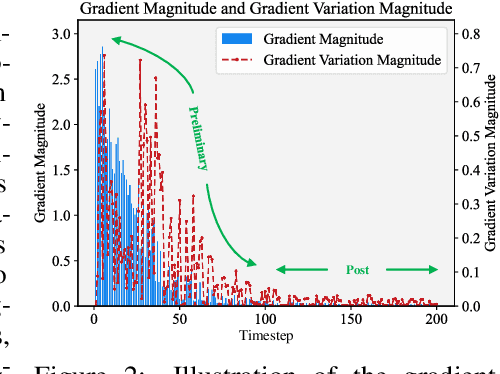
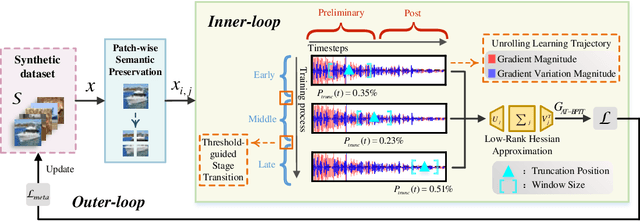
The growing demand for efficient deep learning has positioned dataset distillation as a pivotal technique for compressing training dataset while preserving model performance. However, existing inner-loop optimization methods for dataset distillation typically rely on random truncation strategies, which lack flexibility and often yield suboptimal results. In this work, we observe that neural networks exhibit distinct learning dynamics across different training stages-early, middle, and late-making random truncation ineffective. To address this limitation, we propose Automatic Truncated Backpropagation Through Time (AT-BPTT), a novel framework that dynamically adapts both truncation positions and window sizes according to intrinsic gradient behavior. AT-BPTT introduces three key components: (1) a probabilistic mechanism for stage-aware timestep selection, (2) an adaptive window sizing strategy based on gradient variation, and (3) a low-rank Hessian approximation to reduce computational overhead. Extensive experiments on CIFAR-10, CIFAR-100, Tiny-ImageNet, and ImageNet-1K show that AT-BPTT achieves state-of-the-art performance, improving accuracy by an average of 6.16% over baseline methods. Moreover, our approach accelerates inner-loop optimization by 3.9x while saving 63% memory cost.

RMT-KD: Random Matrix Theoretic Causal Knowledge Distillation

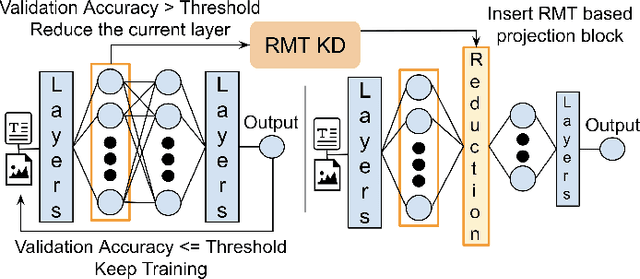
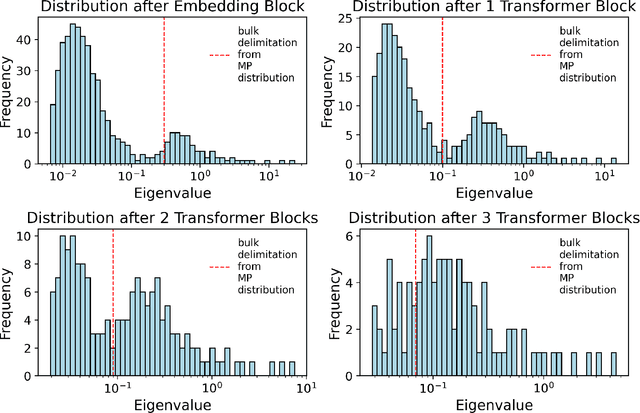
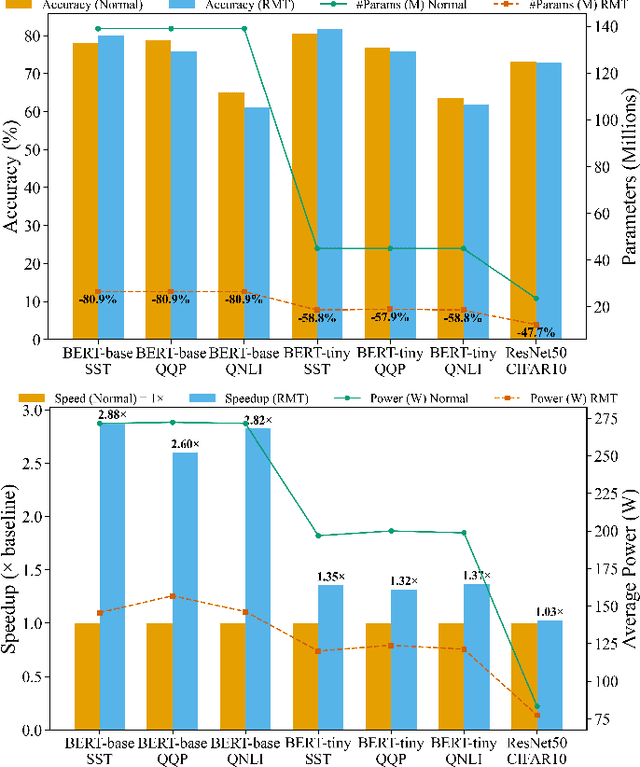
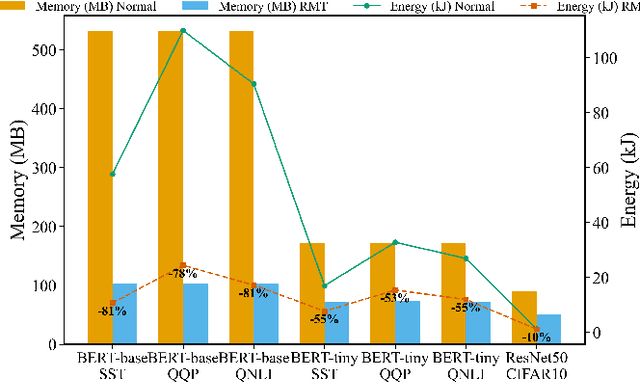
Large deep learning models such as BERT and ResNet achieve state-of-the-art performance but are costly to deploy at the edge due to their size and compute demands. We present RMT-KD, a compression method that leverages Random Matrix Theory (RMT) for knowledge distillation to iteratively reduce network size. Instead of pruning or heuristic rank selection, RMT-KD preserves only informative directions identified via the spectral properties of hidden representations. RMT-based causal reduction is applied layer by layer with self-distillation to maintain stability and accuracy. On GLUE, AG News, and CIFAR-10, RMT-KD achieves up to 80% parameter reduction with only 2% accuracy loss, delivering 2.8x faster inference and nearly halved power consumption. These results establish RMT-KD as a mathematically grounded approach to network distillation.

Explaining Deep Network Classification of Matrices: A Case Study on Monotonicity

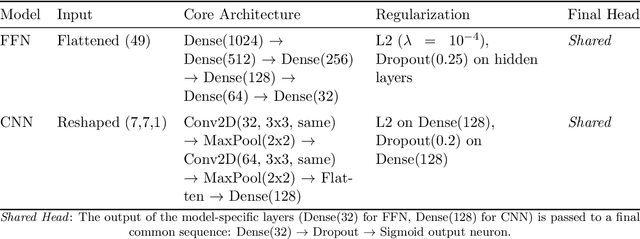
This work demonstrates a methodology for using deep learning to discover simple, practical criteria for classifying matrices based on abstract algebraic properties. By combining a high-performance neural network with explainable AI (XAI) techniques, we can distill a model's learned strategy into human-interpretable rules. We apply this approach to the challenging case of monotone matrices, defined by the condition that their inverses are entrywise nonnegative. Despite their simple definition, an easy characterization in terms of the matrix elements or the derived parameters is not known. Here, we present, to the best of our knowledge, the first systematic machine-learning approach for deriving a practical criterion that distinguishes monotone from non-monotone matrices. After establishing a labelled dataset by randomly generated monotone and non-monotone matrices uniformly on $(-1,1)$, we employ deep neural network algorithms for classifying the matrices as monotone or non-monotone, using both their entries and a comprehensive set of matrix features. By saliency methods, such as integrated gradients, we identify among all features, two matrix parameters which alone provide sufficient information for the matrix classification, with $95\%$ accuracy, namely the absolute values of the two lowest-order coefficients, $c_0$ and $c_1$ of the matrix's characteristic polynomial. A data-driven study of 18,000 random $7\times7$ matrices shows that the monotone class obeys $\lvert c_{0}/c_{1}\rvert\le0.18$ with probability $>99.98\%$; because $\lvert c_{0}/c_{1}\rvert = 1/\mathrm{tr}(A^{-1})$ for monotone $A$, this is equivalent to the simple bound $\mathrm{tr}(A^{-1})\ge5.7$.