Zeyang Li
Seed LiveInterpret 2.0: End-to-end Simultaneous Speech-to-speech Translation with Your Voice
Jul 24, 2025Abstract:Simultaneous Interpretation (SI) represents one of the most daunting frontiers in the translation industry, with product-level automatic systems long plagued by intractable challenges: subpar transcription and translation quality, lack of real-time speech generation, multi-speaker confusion, and translated speech inflation, especially in long-form discourses. In this study, we introduce Seed-LiveInterpret 2.0, an end-to-end SI model that delivers high-fidelity, ultra-low-latency speech-to-speech generation with voice cloning capabilities. As a fully operational product-level solution, Seed-LiveInterpret 2.0 tackles these challenges head-on through our novel duplex speech-to-speech understanding-generating framework. Experimental results demonstrate that through large-scale pretraining and reinforcement learning, the model achieves a significantly better balance between translation accuracy and latency, validated by human interpreters to exceed 70% correctness in complex scenarios. Notably, Seed-LiveInterpret 2.0 outperforms commercial SI solutions by significant margins in translation quality, while slashing the average latency of cloned speech from nearly 10 seconds to a near-real-time 3 seconds, which is around a near 70% reduction that drastically enhances practical usability.
Channel-Aware Constellation Design for Digital OTA Computation
Jan 24, 2025



Abstract:Over-the-air (OTA) computation has emerged as a promising technique for efficiently aggregating data from massive numbers of wireless devices. OTA computations can be performed by analog or digital communications. Analog OTA systems are often constrained by limited function adaptability and their reliance on analog amplitude modulation. On the other hand, digital OTA systems may face limitations such as high computational complexity and limited adaptability to varying network configurations. To address these challenges, this paper proposes a novel digital OTA computation system with a channel-aware constellation design for demodulation mappers. The proposed system dynamically adjusts the constellation based on the channel conditions of participating nodes, enabling reliable computation of various functions. By incorporating channel randomness into the constellation design, the system prevent overlap of constellation points, reduces computational complexity, and mitigates excessive transmit power consumption under poor channel conditions. Numerical results demonstrate that the system achieves reliable NMSE performance across a range of scenarios, offering valuable insights into the choice of signal processing methods and weighting strategies under varying computation point configurations, node counts, and quantization levels. This work advances the state of digital OTA computation by addressing critical challenges in scalability, transmit power consumption, and function adaptability.
Seed-ASR: Understanding Diverse Speech and Contexts with LLM-based Speech Recognition
Jul 05, 2024



Abstract:Modern automatic speech recognition (ASR) model is required to accurately transcribe diverse speech signals (from different domains, languages, accents, etc) given the specific contextual information in various application scenarios. Classic end-to-end models fused with extra language models perform well, but mainly in data matching scenarios and are gradually approaching a bottleneck. In this work, we introduce Seed-ASR, a large language model (LLM) based speech recognition model. Seed-ASR is developed based on the framework of audio conditioned LLM (AcLLM), leveraging the capabilities of LLMs by inputting continuous speech representations together with contextual information into the LLM. Through stage-wise large-scale training and the elicitation of context-aware capabilities in LLM, Seed-ASR demonstrates significant improvement over end-to-end models on comprehensive evaluation sets, including multiple domains, accents/dialects and languages. Additionally, Seed-ASR can be further deployed to support specific needs in various scenarios without requiring extra language models. Compared to recently released large ASR models, Seed-ASR achieves 10%-40% reduction in word (or character, for Chinese) error rates on Chinese and English public test sets, further demonstrating its powerful performance.
Learning Predictive Safety Filter via Decomposition of Robust Invariant Set
Nov 12, 2023


Abstract:Ensuring safety of nonlinear systems under model uncertainty and external disturbances is crucial, especially for real-world control tasks. Predictive methods such as robust model predictive control (RMPC) require solving nonconvex optimization problems online, which leads to high computational burden and poor scalability. Reinforcement learning (RL) works well with complex systems, but pays the price of losing rigorous safety guarantee. This paper presents a theoretical framework that bridges the advantages of both RMPC and RL to synthesize safety filters for nonlinear systems with state- and action-dependent uncertainty. We decompose the robust invariant set (RIS) into two parts: a target set that aligns with terminal region design of RMPC, and a reach-avoid set that accounts for the rest of RIS. We propose a policy iteration approach for robust reach-avoid problems and establish its monotone convergence. This method sets the stage for an adversarial actor-critic deep RL algorithm, which simultaneously synthesizes a reach-avoid policy network, a disturbance policy network, and a reach-avoid value network. The learned reach-avoid policy network is utilized to generate nominal trajectories for online verification, which filters potentially unsafe actions that may drive the system into unsafe regions when worst-case disturbances are applied. We formulate a second-order cone programming (SOCP) approach for online verification using system level synthesis, which optimizes for the worst-case reach-avoid value of any possible trajectories. The proposed safety filter requires much lower computational complexity than RMPC and still enjoys persistent robust safety guarantee. The effectiveness of our method is illustrated through a numerical example.
Robust Safe Reinforcement Learning under Adversarial Disturbances
Oct 11, 2023



Abstract:Safety is a primary concern when applying reinforcement learning to real-world control tasks, especially in the presence of external disturbances. However, existing safe reinforcement learning algorithms rarely account for external disturbances, limiting their applicability and robustness in practice. To address this challenge, this paper proposes a robust safe reinforcement learning framework that tackles worst-case disturbances. First, this paper presents a policy iteration scheme to solve for the robust invariant set, i.e., a subset of the safe set, where persistent safety is only possible for states within. The key idea is to establish a two-player zero-sum game by leveraging the safety value function in Hamilton-Jacobi reachability analysis, in which the protagonist (i.e., control inputs) aims to maintain safety and the adversary (i.e., external disturbances) tries to break down safety. This paper proves that the proposed policy iteration algorithm converges monotonically to the maximal robust invariant set. Second, this paper integrates the proposed policy iteration scheme into a constrained reinforcement learning algorithm that simultaneously synthesizes the robust invariant set and uses it for constrained policy optimization. This algorithm tackles both optimality and safety, i.e., learning a policy that attains high rewards while maintaining safety under worst-case disturbances. Experiments on classic control tasks show that the proposed method achieves zero constraint violation with learned worst-case adversarial disturbances, while other baseline algorithms violate the safety constraints substantially. Our proposed method also attains comparable performance as the baselines even in the absence of the adversary.
Bridging the Gap between Newton-Raphson Method and Regularized Policy Iteration
Oct 11, 2023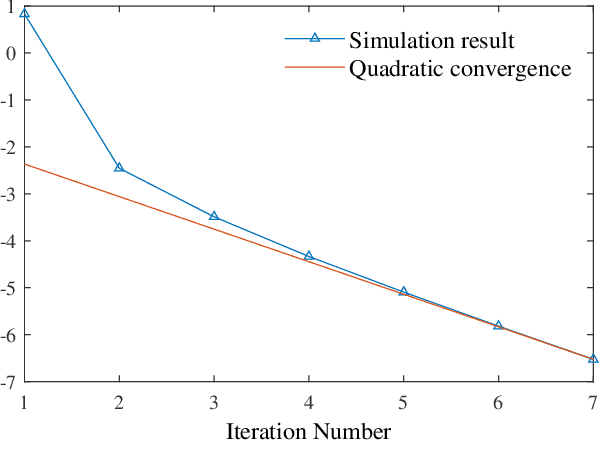
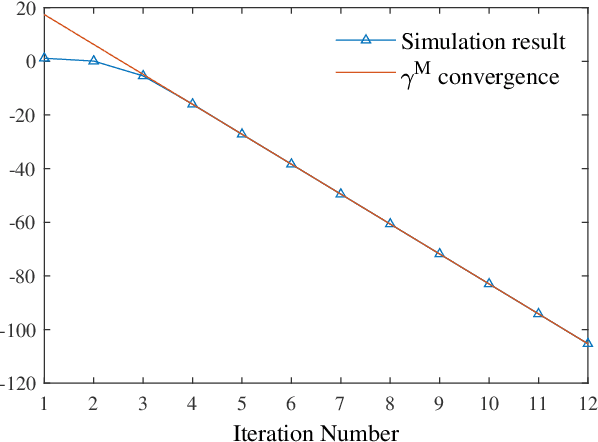
Abstract:Regularization is one of the most important techniques in reinforcement learning algorithms. The well-known soft actor-critic algorithm is a special case of regularized policy iteration where the regularizer is chosen as Shannon entropy. Despite some empirical success of regularized policy iteration, its theoretical underpinnings remain unclear. This paper proves that regularized policy iteration is strictly equivalent to the standard Newton-Raphson method in the condition of smoothing out Bellman equation with strongly convex functions. This equivalence lays the foundation of a unified analysis for both global and local convergence behaviors of regularized policy iteration. We prove that regularized policy iteration has global linear convergence with the rate being $\gamma$ (discount factor). Furthermore, this algorithm converges quadratically once it enters a local region around the optimal value. We also show that a modified version of regularized policy iteration, i.e., with finite-step policy evaluation, is equivalent to inexact Newton method where the Newton iteration formula is solved with truncated iterations. We prove that the associated algorithm achieves an asymptotic linear convergence rate of $\gamma^M$ in which $M$ denotes the number of steps carried out in policy evaluation. Our results take a solid step towards a better understanding of the convergence properties of regularized policy iteration algorithms.
Safe Reinforcement Learning with Dual Robustness
Sep 13, 2023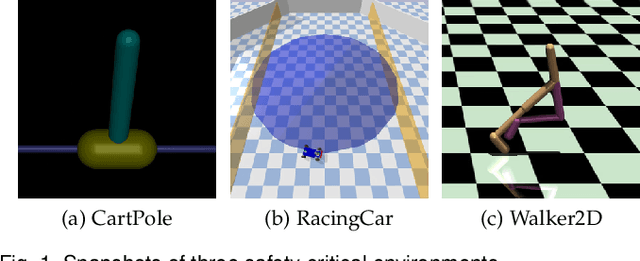
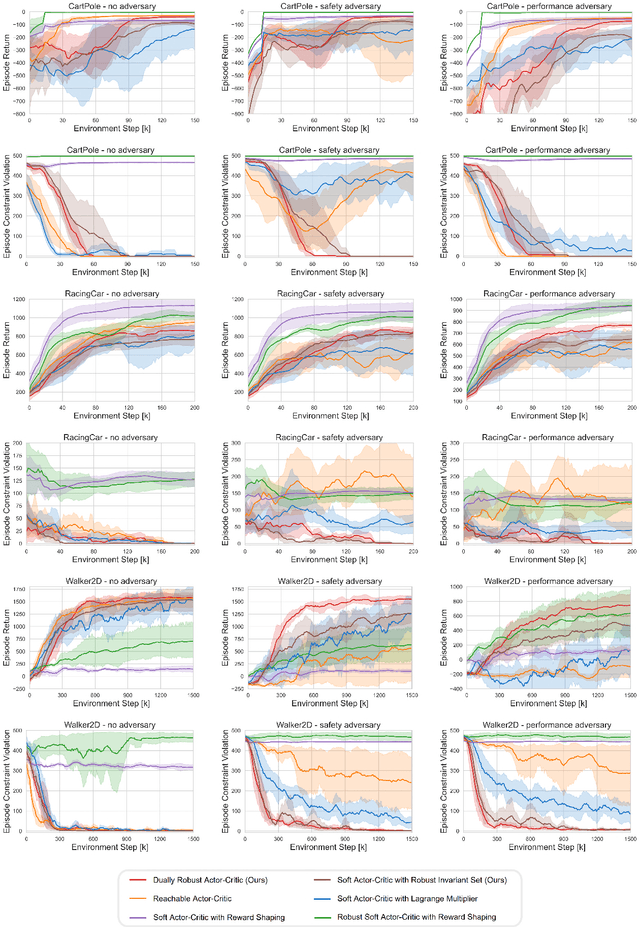
Abstract:Reinforcement learning (RL) agents are vulnerable to adversarial disturbances, which can deteriorate task performance or compromise safety specifications. Existing methods either address safety requirements under the assumption of no adversary (e.g., safe RL) or only focus on robustness against performance adversaries (e.g., robust RL). Learning one policy that is both safe and robust remains a challenging open problem. The difficulty is how to tackle two intertwined aspects in the worst cases: feasibility and optimality. Optimality is only valid inside a feasible region, while identification of maximal feasible region must rely on learning the optimal policy. To address this issue, we propose a systematic framework to unify safe RL and robust RL, including problem formulation, iteration scheme, convergence analysis and practical algorithm design. This unification is built upon constrained two-player zero-sum Markov games. A dual policy iteration scheme is proposed, which simultaneously optimizes a task policy and a safety policy. The convergence of this iteration scheme is proved. Furthermore, we design a deep RL algorithm for practical implementation, called dually robust actor-critic (DRAC). The evaluations with safety-critical benchmarks demonstrate that DRAC achieves high performance and persistent safety under all scenarios (no adversary, safety adversary, performance adversary), outperforming all baselines significantly.
Smoothing Policy Iteration for Zero-sum Markov Games
Dec 03, 2022



Abstract:Zero-sum Markov Games (MGs) has been an efficient framework for multi-agent systems and robust control, wherein a minimax problem is constructed to solve the equilibrium policies. At present, this formulation is well studied under tabular settings wherein the maximum operator is primarily and exactly solved to calculate the worst-case value function. However, it is non-trivial to extend such methods to handle complex tasks, as finding the maximum over large-scale action spaces is usually cumbersome. In this paper, we propose the smoothing policy iteration (SPI) algorithm to solve the zero-sum MGs approximately, where the maximum operator is replaced by the weighted LogSumExp (WLSE) function to obtain the nearly optimal equilibrium policies. Specially, the adversarial policy is served as the weight function to enable an efficient sampling over action spaces.We also prove the convergence of SPI and analyze its approximation error in $\infty -$norm based on the contraction mapping theorem. Besides, we propose a model-based algorithm called Smooth adversarial Actor-critic (SaAC) by extending SPI with the function approximations. The target value related to WLSE function is evaluated by the sampled trajectories and then mean square error is constructed to optimize the value function, and the gradient-ascent-descent methods are adopted to optimize the protagonist and adversarial policies jointly. In addition, we incorporate the reparameterization technique in model-based gradient back-propagation to prevent the gradient vanishing due to sampling from the stochastic policies. We verify our algorithm in both tabular and function approximation settings. Results show that SPI can approximate the worst-case value function with a high accuracy and SaAC can stabilize the training process and improve the adversarial robustness in a large margin.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge