Chuxiong Hu
Learning Predictive Safety Filter via Decomposition of Robust Invariant Set
Nov 12, 2023


Abstract:Ensuring safety of nonlinear systems under model uncertainty and external disturbances is crucial, especially for real-world control tasks. Predictive methods such as robust model predictive control (RMPC) require solving nonconvex optimization problems online, which leads to high computational burden and poor scalability. Reinforcement learning (RL) works well with complex systems, but pays the price of losing rigorous safety guarantee. This paper presents a theoretical framework that bridges the advantages of both RMPC and RL to synthesize safety filters for nonlinear systems with state- and action-dependent uncertainty. We decompose the robust invariant set (RIS) into two parts: a target set that aligns with terminal region design of RMPC, and a reach-avoid set that accounts for the rest of RIS. We propose a policy iteration approach for robust reach-avoid problems and establish its monotone convergence. This method sets the stage for an adversarial actor-critic deep RL algorithm, which simultaneously synthesizes a reach-avoid policy network, a disturbance policy network, and a reach-avoid value network. The learned reach-avoid policy network is utilized to generate nominal trajectories for online verification, which filters potentially unsafe actions that may drive the system into unsafe regions when worst-case disturbances are applied. We formulate a second-order cone programming (SOCP) approach for online verification using system level synthesis, which optimizes for the worst-case reach-avoid value of any possible trajectories. The proposed safety filter requires much lower computational complexity than RMPC and still enjoys persistent robust safety guarantee. The effectiveness of our method is illustrated through a numerical example.
Robust Safe Reinforcement Learning under Adversarial Disturbances
Oct 11, 2023



Abstract:Safety is a primary concern when applying reinforcement learning to real-world control tasks, especially in the presence of external disturbances. However, existing safe reinforcement learning algorithms rarely account for external disturbances, limiting their applicability and robustness in practice. To address this challenge, this paper proposes a robust safe reinforcement learning framework that tackles worst-case disturbances. First, this paper presents a policy iteration scheme to solve for the robust invariant set, i.e., a subset of the safe set, where persistent safety is only possible for states within. The key idea is to establish a two-player zero-sum game by leveraging the safety value function in Hamilton-Jacobi reachability analysis, in which the protagonist (i.e., control inputs) aims to maintain safety and the adversary (i.e., external disturbances) tries to break down safety. This paper proves that the proposed policy iteration algorithm converges monotonically to the maximal robust invariant set. Second, this paper integrates the proposed policy iteration scheme into a constrained reinforcement learning algorithm that simultaneously synthesizes the robust invariant set and uses it for constrained policy optimization. This algorithm tackles both optimality and safety, i.e., learning a policy that attains high rewards while maintaining safety under worst-case disturbances. Experiments on classic control tasks show that the proposed method achieves zero constraint violation with learned worst-case adversarial disturbances, while other baseline algorithms violate the safety constraints substantially. Our proposed method also attains comparable performance as the baselines even in the absence of the adversary.
Bridging the Gap between Newton-Raphson Method and Regularized Policy Iteration
Oct 11, 2023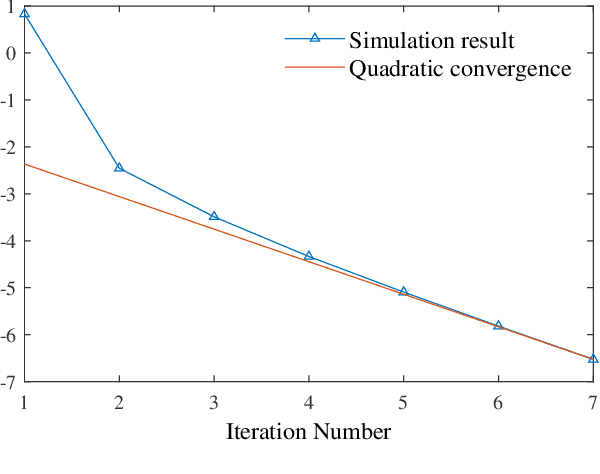
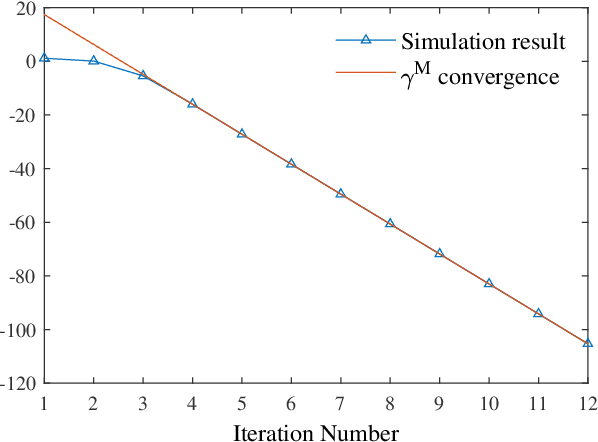
Abstract:Regularization is one of the most important techniques in reinforcement learning algorithms. The well-known soft actor-critic algorithm is a special case of regularized policy iteration where the regularizer is chosen as Shannon entropy. Despite some empirical success of regularized policy iteration, its theoretical underpinnings remain unclear. This paper proves that regularized policy iteration is strictly equivalent to the standard Newton-Raphson method in the condition of smoothing out Bellman equation with strongly convex functions. This equivalence lays the foundation of a unified analysis for both global and local convergence behaviors of regularized policy iteration. We prove that regularized policy iteration has global linear convergence with the rate being $\gamma$ (discount factor). Furthermore, this algorithm converges quadratically once it enters a local region around the optimal value. We also show that a modified version of regularized policy iteration, i.e., with finite-step policy evaluation, is equivalent to inexact Newton method where the Newton iteration formula is solved with truncated iterations. We prove that the associated algorithm achieves an asymptotic linear convergence rate of $\gamma^M$ in which $M$ denotes the number of steps carried out in policy evaluation. Our results take a solid step towards a better understanding of the convergence properties of regularized policy iteration algorithms.
Safe Reinforcement Learning with Dual Robustness
Sep 13, 2023
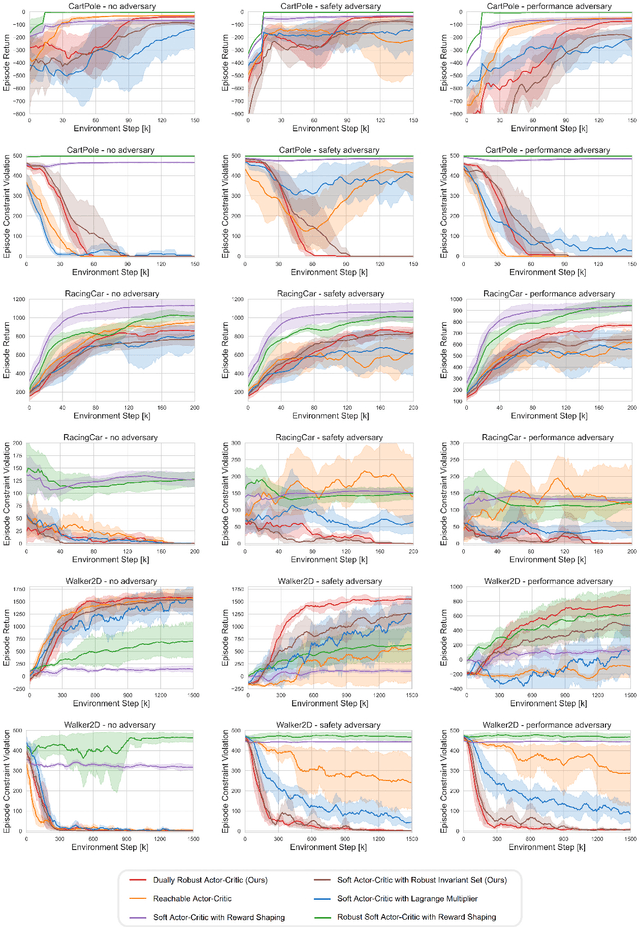
Abstract:Reinforcement learning (RL) agents are vulnerable to adversarial disturbances, which can deteriorate task performance or compromise safety specifications. Existing methods either address safety requirements under the assumption of no adversary (e.g., safe RL) or only focus on robustness against performance adversaries (e.g., robust RL). Learning one policy that is both safe and robust remains a challenging open problem. The difficulty is how to tackle two intertwined aspects in the worst cases: feasibility and optimality. Optimality is only valid inside a feasible region, while identification of maximal feasible region must rely on learning the optimal policy. To address this issue, we propose a systematic framework to unify safe RL and robust RL, including problem formulation, iteration scheme, convergence analysis and practical algorithm design. This unification is built upon constrained two-player zero-sum Markov games. A dual policy iteration scheme is proposed, which simultaneously optimizes a task policy and a safety policy. The convergence of this iteration scheme is proved. Furthermore, we design a deep RL algorithm for practical implementation, called dually robust actor-critic (DRAC). The evaluations with safety-critical benchmarks demonstrate that DRAC achieves high performance and persistent safety under all scenarios (no adversary, safety adversary, performance adversary), outperforming all baselines significantly.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge