Group-Graph Policy Optimization for Long-Horizon Agentic Reinforcement Learning

Group-based Reinforcement Learning (RL) has significantly enhanced Large Language Models (LLMs) in agentic scenarios. To achieve finer-grained policy updates, recent agentic RL frameworks have shifted from trajectory-level to step-level training. However, long-horizon agentic RL suffers from severe reward sparsity and delay, as feedback is often deferred for dozens of interaction steps. While existing step-level frameworks refine training granularity, their credit assignment remains coarse-grained and still treats agent exploration as isolated, linear trajectories. This oversimplified perspective ignores the inherent graph structure of state transitions, leading to high-variance state-value estimation and myopic, localized credit assignment. To overcome these critical bottlenecks, we propose Group-Graph Policy Optimization (G2PO), a novel group-based RL algorithm tailored for multi-turn agentic tasks. G2PO explicitly transforms linear interaction trajectories into a global state-transition graph. By aggregating identical observations across different trajectories, we introduce group-aggregation state-value estimation that reduces sampling variance and trajectory-dependent bias. Furthermore, we redefine agent actions as transitions between state nodes and propose an edge-centric advantage estimation strategy. By globally standardizing Temporal Difference (TD) errors across the entire graph, G2PO explicitly identifies and prioritizes critical transitions that drive absolute task progress. Extensive experiments on representative long-horizon benchmarks-WebShop, ALFWorld, and AppWorld-demonstrate that G2PO substantially outperforms state-of-the-art prompt-based and RL baselines, achieving remarkable success rate improvements of up to 22.2% over GRPO.

Multimodal Fake News Detection: MFND Dataset and Shallow-Deep Multitask Learning

Multimodal news contains a wealth of information and is easily affected by deepfake modeling attacks. To combat the latest image and text generation methods, we present a new Multimodal Fake News Detection dataset (MFND) containing 11 manipulated types, designed to detect and localize highly authentic fake news. Furthermore, we propose a Shallow-Deep Multitask Learning (SDML) model for fake news, which fully uses unimodal and mutual modal features to mine the intrinsic semantics of news. Under shallow inference, we propose the momentum distillation-based light punishment contrastive learning for fine-grained uniform spatial image and text semantic alignment, and an adaptive cross-modal fusion module to enhance mutual modal features. Under deep inference, we design a two-branch framework to augment the image and text unimodal features, respectively merging with mutual modalities features, for four predictions via dedicated detection and localization projections. Experiments on both mainstream and our proposed datasets demonstrate the superiority of the model. Codes and dataset are released at https://github.com/yunan-wang33/sdml.

InCo-DPO: Balancing Distribution Shift and Data Quality for Enhanced Preference Optimization

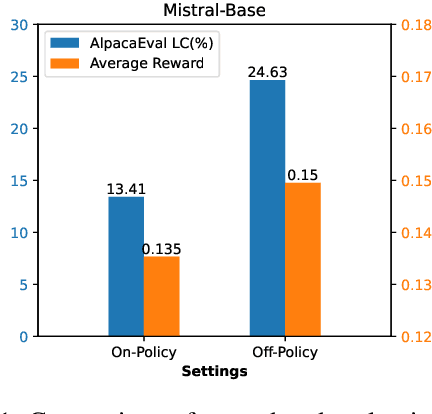
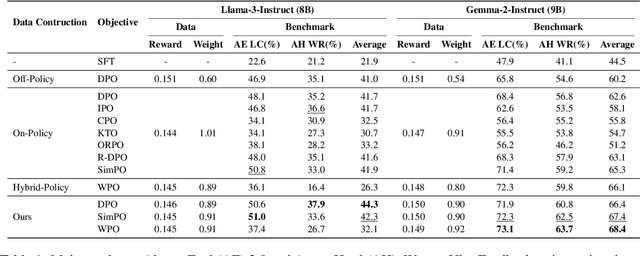
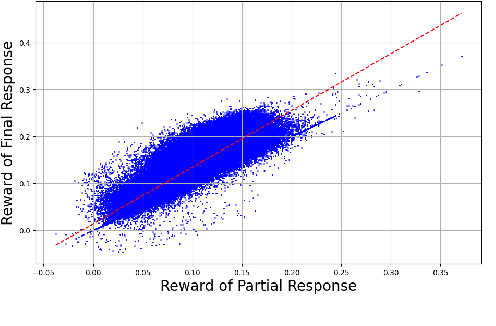
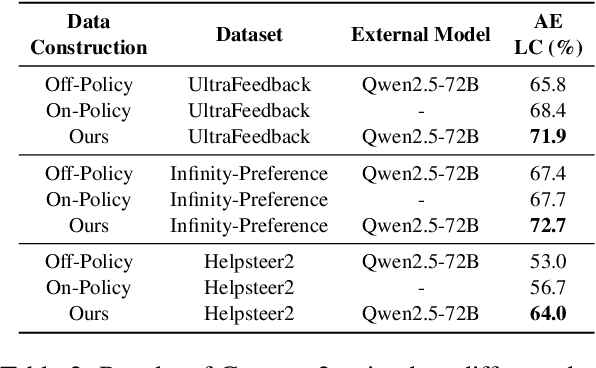
Direct Preference Optimization (DPO) optimizes language models to align with human preferences. Utilizing on-policy samples, generated directly by the policy model, typically results in better performance due to its distribution consistency with the model compared to off-policy samples. This paper identifies the quality of candidate preference samples as another critical factor. While the quality of on-policy data is inherently constrained by the capabilities of the policy model, off-policy data, which can be derived from diverse sources, offers greater potential for quality despite experiencing distribution shifts. However, current research mostly relies on on-policy data and neglects the value of off-policy data in terms of data quality, due to the challenge posed by distribution shift. In this paper, we propose InCo-DPO, an efficient method for synthesizing preference data by integrating on-policy and off-policy data, allowing dynamic adjustments to balance distribution shifts and data quality, thus finding an optimal trade-off. Consequently, InCo-DPO overcomes the limitations of distribution shifts in off-policy data and the quality constraints of on-policy data. We evaluated InCo-DPO with the Alpaca-Eval 2.0 and Arena-Hard benchmarks. Experimental results demonstrate that our approach not only outperforms both on-policy and off-policy data but also achieves a state-of-the-art win rate of 60.8 on Arena-Hard with the vanilla DPO using Gemma-2 model.

Single picture single photon single pixel 3D imaging through unknown thick scattering medium

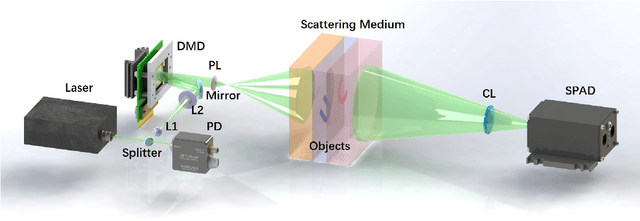
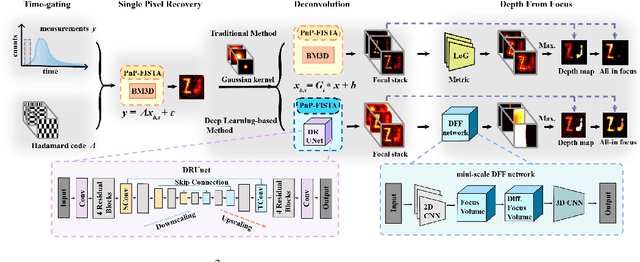
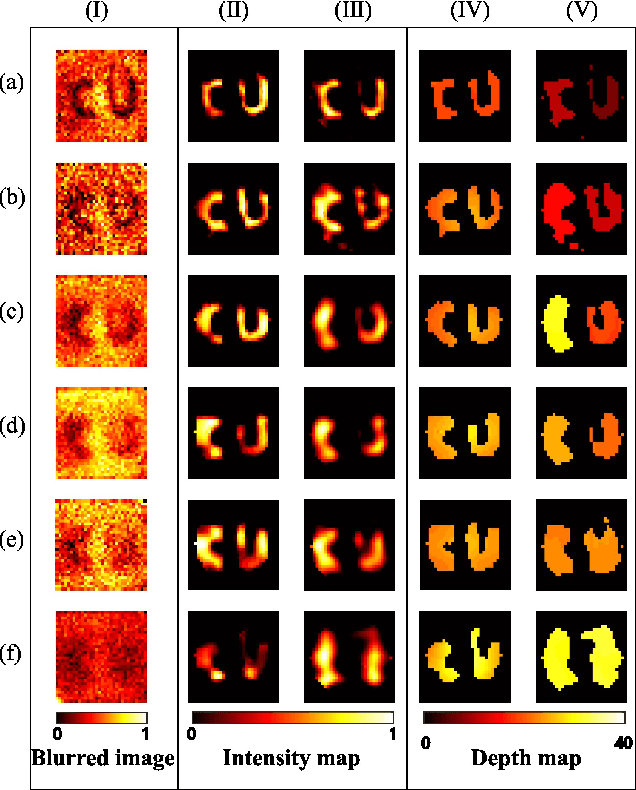
Imaging through thick scattering media presents significant challenges, particularly for three-dimensional (3D) applications. This manuscript demonstrates a novel scheme for single-image-enabled 3D imaging through such media, treating the scattering medium as a lens. This approach captures a comprehensive image containing information about objects hidden at various depths. By leveraging depth from focus and the reduced thickness of the scattering medium for single-pixel imaging, the proposed method ensures robust 3D imaging capabilities. We develop both traditional metric-based and deep learning-based methods to extract depth information for each pixel, allowing us to explore the locations of both positive and negative objects, whether shallow or deep. Remarkably, this scheme enables the simultaneous 3D reconstruction of targets concealed within the scattering medium. Specifically, we successfully reconstructed targets buried at depths of 5 mm and 30 mm within a total medium thickness of 60 mm. Additionally, we can effectively distinguish targets at three different depths. Notably, this scheme requires no prior knowledge of the scattering medium, no invasive procedures, reference measurements, or calibration.

Bridging the Gap between Newton-Raphson Method and Regularized Policy Iteration

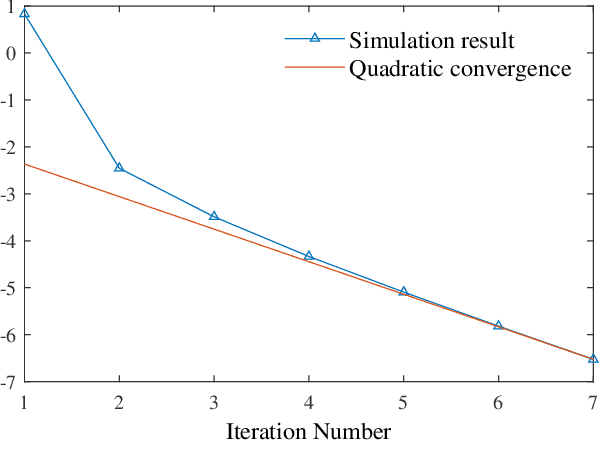
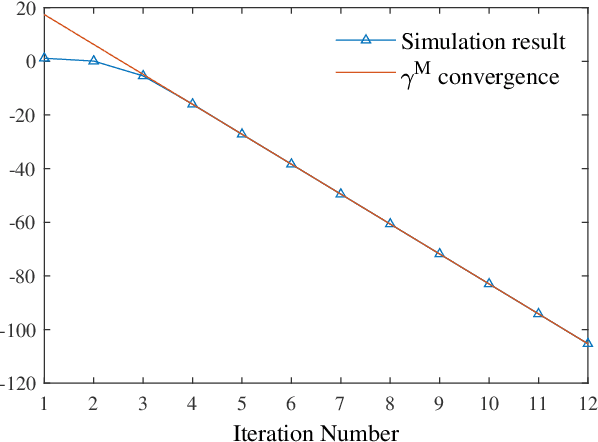
Regularization is one of the most important techniques in reinforcement learning algorithms. The well-known soft actor-critic algorithm is a special case of regularized policy iteration where the regularizer is chosen as Shannon entropy. Despite some empirical success of regularized policy iteration, its theoretical underpinnings remain unclear. This paper proves that regularized policy iteration is strictly equivalent to the standard Newton-Raphson method in the condition of smoothing out Bellman equation with strongly convex functions. This equivalence lays the foundation of a unified analysis for both global and local convergence behaviors of regularized policy iteration. We prove that regularized policy iteration has global linear convergence with the rate being $\gamma$ (discount factor). Furthermore, this algorithm converges quadratically once it enters a local region around the optimal value. We also show that a modified version of regularized policy iteration, i.e., with finite-step policy evaluation, is equivalent to inexact Newton method where the Newton iteration formula is solved with truncated iterations. We prove that the associated algorithm achieves an asymptotic linear convergence rate of $\gamma^M$ in which $M$ denotes the number of steps carried out in policy evaluation. Our results take a solid step towards a better understanding of the convergence properties of regularized policy iteration algorithms.

Robust Safe Reinforcement Learning under Adversarial Disturbances

Safety is a primary concern when applying reinforcement learning to real-world control tasks, especially in the presence of external disturbances. However, existing safe reinforcement learning algorithms rarely account for external disturbances, limiting their applicability and robustness in practice. To address this challenge, this paper proposes a robust safe reinforcement learning framework that tackles worst-case disturbances. First, this paper presents a policy iteration scheme to solve for the robust invariant set, i.e., a subset of the safe set, where persistent safety is only possible for states within. The key idea is to establish a two-player zero-sum game by leveraging the safety value function in Hamilton-Jacobi reachability analysis, in which the protagonist (i.e., control inputs) aims to maintain safety and the adversary (i.e., external disturbances) tries to break down safety. This paper proves that the proposed policy iteration algorithm converges monotonically to the maximal robust invariant set. Second, this paper integrates the proposed policy iteration scheme into a constrained reinforcement learning algorithm that simultaneously synthesizes the robust invariant set and uses it for constrained policy optimization. This algorithm tackles both optimality and safety, i.e., learning a policy that attains high rewards while maintaining safety under worst-case disturbances. Experiments on classic control tasks show that the proposed method achieves zero constraint violation with learned worst-case adversarial disturbances, while other baseline algorithms violate the safety constraints substantially. Our proposed method also attains comparable performance as the baselines even in the absence of the adversary.

Safe Reinforcement Learning with Dual Robustness

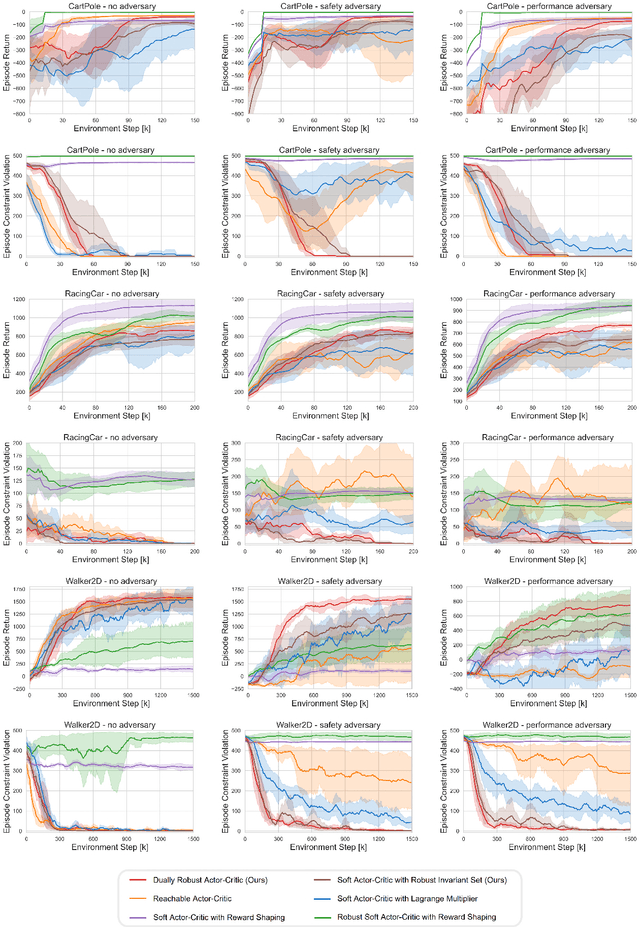
Reinforcement learning (RL) agents are vulnerable to adversarial disturbances, which can deteriorate task performance or compromise safety specifications. Existing methods either address safety requirements under the assumption of no adversary (e.g., safe RL) or only focus on robustness against performance adversaries (e.g., robust RL). Learning one policy that is both safe and robust remains a challenging open problem. The difficulty is how to tackle two intertwined aspects in the worst cases: feasibility and optimality. Optimality is only valid inside a feasible region, while identification of maximal feasible region must rely on learning the optimal policy. To address this issue, we propose a systematic framework to unify safe RL and robust RL, including problem formulation, iteration scheme, convergence analysis and practical algorithm design. This unification is built upon constrained two-player zero-sum Markov games. A dual policy iteration scheme is proposed, which simultaneously optimizes a task policy and a safety policy. The convergence of this iteration scheme is proved. Furthermore, we design a deep RL algorithm for practical implementation, called dually robust actor-critic (DRAC). The evaluations with safety-critical benchmarks demonstrate that DRAC achieves high performance and persistent safety under all scenarios (no adversary, safety adversary, performance adversary), outperforming all baselines significantly.