Yuhai Tu
On the Superlinear Relationship between SGD Noise Covariance and Loss Landscape Curvature
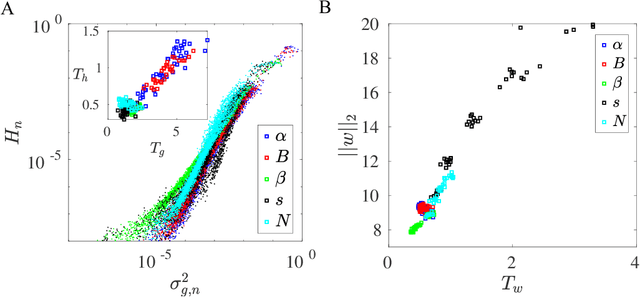
Feb 05, 2026Abstract:Stochastic Gradient Descent (SGD) introduces anisotropic noise that is correlated with the local curvature of the loss landscape, thereby biasing optimization toward flat minima. Prior work often assumes an equivalence between the Fisher Information Matrix and the Hessian for negative log-likelihood losses, leading to the claim that the SGD noise covariance $\mathbf{C}$ is proportional to the Hessian $\mathbf{H}$. We show that this assumption holds only under restrictive conditions that are typically violated in deep neural networks. Using the recently discovered Activity--Weight Duality, we find a more general relationship agnostic to the specific loss formulation, showing that $\mathbf{C} \propto \mathbb{E}_p[\mathbf{h}_p^2]$, where $\mathbf{h}_p$ denotes the per-sample Hessian with $\mathbf{H} = \mathbb{E}_p[\mathbf{h}_p]$. As a consequence, $\mathbf{C}$ and $\mathbf{H}$ commute approximately rather than coincide exactly, and their diagonal elements follow an approximate power-law relation $C_{ii} \propto H_{ii}^γ$ with a theoretically bounded exponent $1 \leq γ\leq 2$, determined by per-sample Hessian spectra. Experiments across datasets, architectures, and loss functions validate these bounds, providing a unified characterization of the noise-curvature relationship in deep learning.
Transient learning dynamics drive escape from sharp valleys in Stochastic Gradient Descent
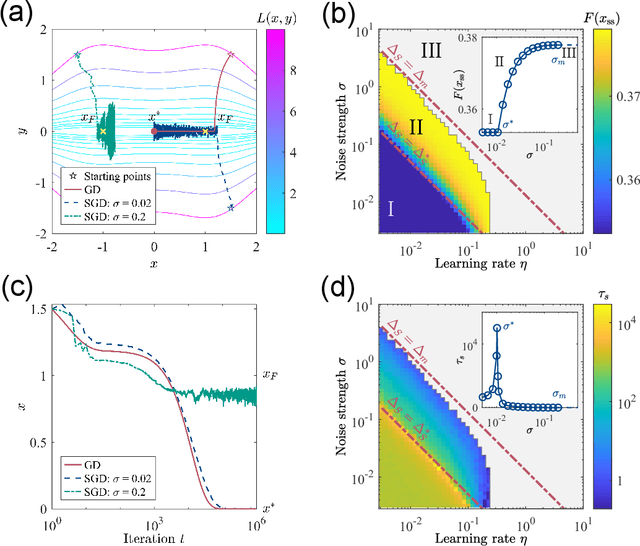
Jan 16, 2026Abstract:Stochastic gradient descent (SGD) is central to deep learning, yet the dynamical origin of its preference for flatter, more generalizable solutions remains unclear. Here, by analyzing SGD learning dynamics, we identify a nonequilibrium mechanism governing solution selection. Numerical experiments reveal a transient exploratory phase in which SGD trajectories repeatedly escape sharp valleys and transition toward flatter regions of the loss landscape. By using a tractable physical model, we show that the SGD noise reshapes the landscape into an effective potential that favors flat solutions. Crucially, we uncover a transient freezing mechanism: as training proceeds, growing energy barriers suppress inter-valley transitions and ultimately trap the dynamics within a single basin. Increasing the SGD noise strength delays this freezing, which enhances convergence to flatter minima. Together, these results provide a unified physical framework linking learning dynamics, loss-landscape geometry, and generalization, and suggest principles for the design of more effective optimization algorithms.
Maximal Domain Independent Representations Improve Transfer Learning
Jun 01, 2023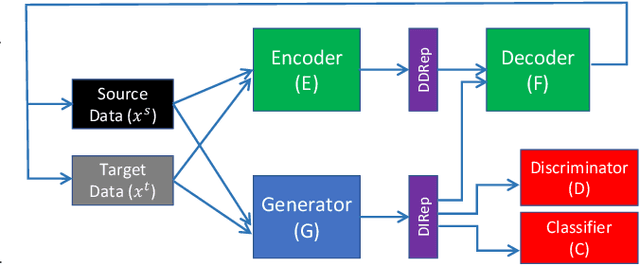
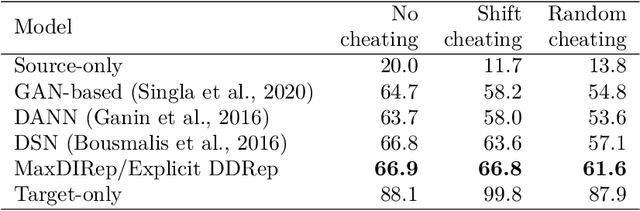
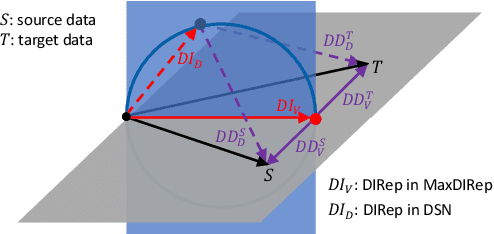

Abstract:Domain adaptation (DA) adapts a training dataset from a source domain for use in a learning task in a target domain in combination with data available at the target. One popular approach for DA is to create a domain-independent representation (DIRep) learned by a generator from all input samples and then train a classifier on top of it using all labeled samples. A domain discriminator is added to train the generator adversarially to exclude domain specific features from the DIRep. However, this approach tends to generate insufficient information for accurate classification learning. In this paper, we present a novel approach that integrates the adversarial model with a variational autoencoder. In addition to the DIRep, we introduce a domain-dependent representation (DDRep) such that information from both DIRep and DDRep is sufficient to reconstruct samples from both domains. We further penalize the size of the DDRep to drive as much information as possible to the DIRep, which maximizes the accuracy of the classifier in labeling samples in both domains. We empirically evaluate our model using synthetic datasets and demonstrate that spurious class-related features introduced in the source domain are successfully absorbed by the DDRep. This leaves a rich and clean DIRep for accurate transfer learning in the target domain. We further demonstrate its superior performance against other algorithms for a number of common image datasets. We also show we can take advantage of pretrained models.
Effective Dynamics of Generative Adversarial Networks
Dec 08, 2022Abstract:Generative adversarial networks (GANs) are a class of machine-learning models that use adversarial training to generate new samples with the same (potentially very complex) statistics as the training samples. One major form of training failure, known as mode collapse, involves the generator failing to reproduce the full diversity of modes in the target probability distribution. Here, we present an effective model of GAN training, which captures the learning dynamics by replacing the generator neural network with a collection of particles in the output space; particles are coupled by a universal kernel valid for certain wide neural networks and high-dimensional inputs. The generality of our simplified model allows us to study the conditions under which mode collapse occurs. Indeed, experiments which vary the effective kernel of the generator reveal a mode collapse transition, the shape of which can be related to the type of discriminator through the frequency principle. Further, we find that gradient regularizers of intermediate strengths can optimally yield convergence through critical damping of the generator dynamics. Our effective GAN model thus provides an interpretable physical framework for understanding and improving adversarial training.
Stochastic gradient descent introduces an effective landscape-dependent regularization favoring flat solutions
Jun 02, 2022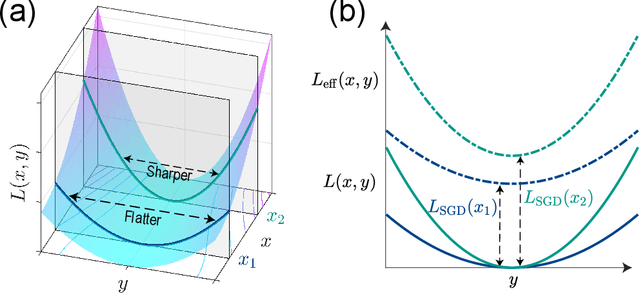
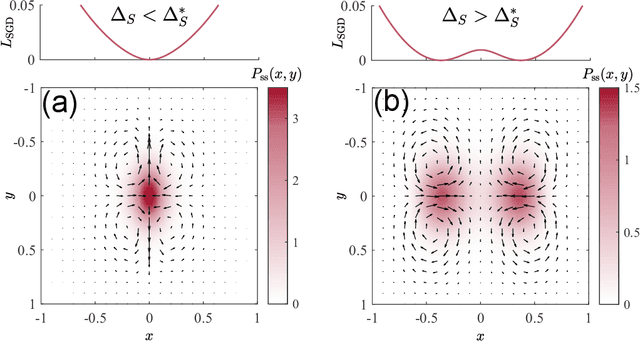
Abstract:Generalization is one of the most important problems in deep learning (DL). In the overparameterized regime in neural networks, there exist many low-loss solutions that fit the training data equally well. The key question is which solution is more generalizable. Empirical studies showed a strong correlation between flatness of the loss landscape at a solution and its generalizability, and stochastic gradient descent (SGD) is crucial in finding the flat solutions. To understand how SGD drives the learning system to flat solutions, we construct a simple model whose loss landscape has a continuous set of degenerate (or near degenerate) minima. By solving the Fokker-Planck equation of the underlying stochastic learning dynamics, we show that due to its strong anisotropy the SGD noise introduces an additional effective loss term that decreases with flatness and has an overall strength that increases with the learning rate and batch-to-batch variation. We find that the additional landscape-dependent SGD-loss breaks the degeneracy and serves as an effective regularization for finding flat solutions. Furthermore, a stronger SGD noise shortens the convergence time to the flat solutions. However, we identify an upper bound for the SGD noise beyond which the system fails to converge. Our results not only elucidate the role of SGD for generalization they may also have important implications for hyperparameter selection for learning efficiently without divergence.
The activity-weight duality in feed forward neural networks: The geometric determinants of generalization
Mar 22, 2022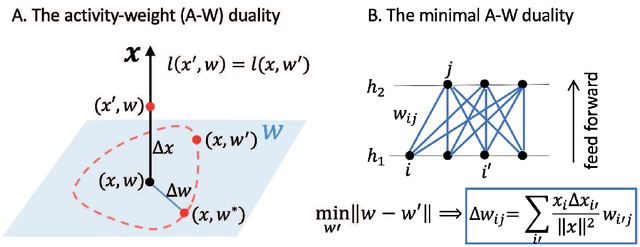
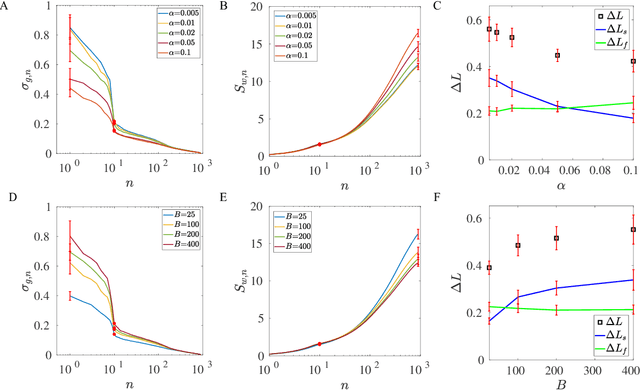

Abstract:One of the fundamental problems in machine learning is generalization. In neural network models with a large number of weights (parameters), many solutions can be found to fit the training data equally well. The key question is which solution can describe testing data not in the training set. Here, we report the discovery of an exact duality (equivalence) between changes in activities in a given layer of neurons and changes in weights that connect to the next layer of neurons in a densely connected layer in any feed forward neural network. The activity-weight (A-W) duality allows us to map variations in inputs (data) to variations of the corresponding dual weights. By using this mapping, we show that the generalization loss can be decomposed into a sum of contributions from different eigen-directions of the Hessian matrix of the loss function at the solution in weight space. The contribution from a given eigen-direction is the product of two geometric factors (determinants): the sharpness of the loss landscape and the standard deviation of the dual weights, which is found to scale with the weight norm of the solution. Our results provide an unified framework, which we used to reveal how different regularization schemes (weight decay, stochastic gradient descent with different batch sizes and learning rates, dropout), training data size, and labeling noise affect generalization performance by controlling either one or both of these two geometric determinants for generalization. These insights can be used to guide development of algorithms for finding more generalizable solutions in overparametrized neural networks.
Loss Landscape Dependent Self-Adjusting Learning Rates in Decentralized Stochastic Gradient Descent
Dec 02, 2021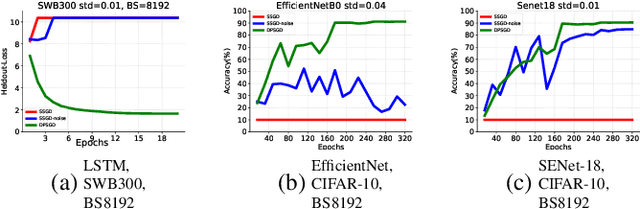
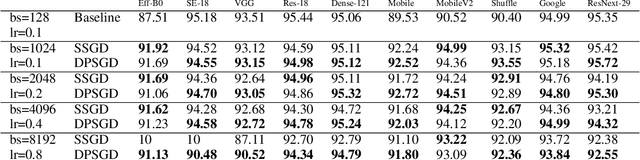
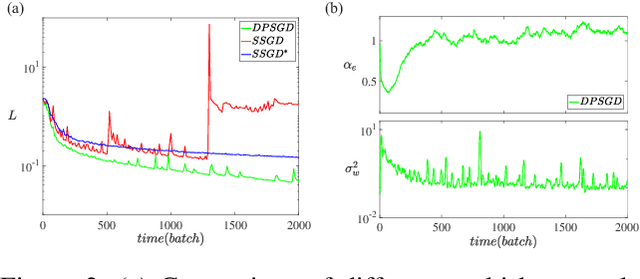
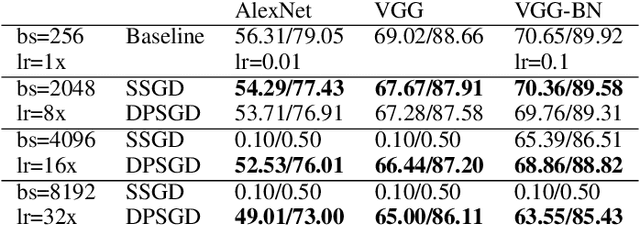
Abstract:Distributed Deep Learning (DDL) is essential for large-scale Deep Learning (DL) training. Synchronous Stochastic Gradient Descent (SSGD) 1 is the de facto DDL optimization method. Using a sufficiently large batch size is critical to achieving DDL runtime speedup. In a large batch setting, the learning rate must be increased to compensate for the reduced number of parameter updates. However, a large learning rate may harm convergence in SSGD and training could easily diverge. Recently, Decentralized Parallel SGD (DPSGD) has been proposed to improve distributed training speed. In this paper, we find that DPSGD not only has a system-wise run-time benefit but also a significant convergence benefit over SSGD in the large batch setting. Based on a detailed analysis of the DPSGD learning dynamics, we find that DPSGD introduces additional landscape-dependent noise that automatically adjusts the effective learning rate to improve convergence. In addition, we theoretically show that this noise smoothes the loss landscape, hence allowing a larger learning rate. We conduct extensive studies over 18 state-of-the-art DL models/tasks and demonstrate that DPSGD often converges in cases where SSGD diverges for large learning rates in the large batch setting. Our findings are consistent across two different application domains: Computer Vision (CIFAR10 and ImageNet-1K) and Automatic Speech Recognition (SWB300 and SWB2000), and two different types of neural network models: Convolutional Neural Networks and Long Short-Term Memory Recurrent Neural Networks.
Phases of learning dynamics in artificial neural networks: with or without mislabeled data
Jan 16, 2021
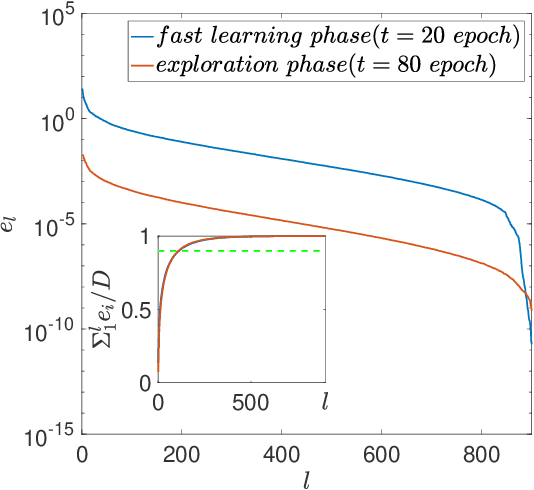

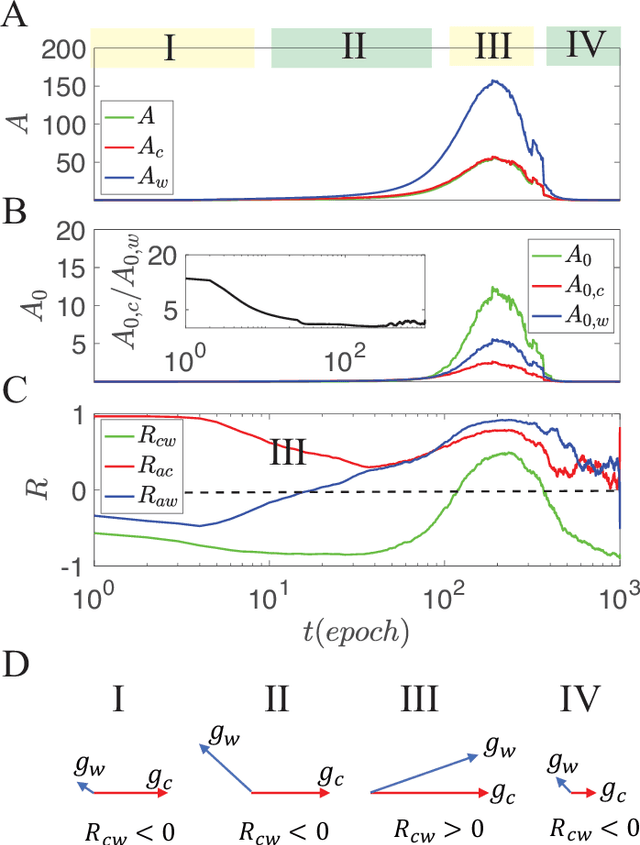
Abstract:Despite tremendous success of deep neural network in machine learning, the underlying reason for its superior learning capability remains unclear. Here, we present a framework based on statistical physics to study dynamics of stochastic gradient descent (SGD) that drives learning in neural networks. By using the minibatch gradient ensemble, we construct order parameters to characterize dynamics of weight updates in SGD. Without mislabeled data, we find that the SGD learning dynamics transitions from a fast learning phase to a slow exploration phase, which is associated with large changes in order parameters that characterize the alignment of SGD gradients and their mean amplitude. In the case with randomly mislabeled samples, SGD learning dynamics falls into four distinct phases. The system first finds solutions for the correctly labeled samples in phase I, it then wanders around these solutions in phase II until it finds a direction to learn the mislabeled samples during phase III, after which it finds solutions that satisfy all training samples during phase IV. Correspondingly, the test error decreases during phase I and remains low during phase II; however, it increases during phase III and reaches a high plateau during phase IV. The transitions between different phases can be understood by changes of order parameters that characterize the alignment of mean gradients for the correctly and incorrectly labeled samples and their (relative) strength during learning. We find that individual sample losses for the two datasets are most separated during phase II, which leads to a cleaning process to eliminate mislabeled samples for improving generalization.
How neural networks find generalizable solutions: Self-tuned annealing in deep learning
Jan 06, 2020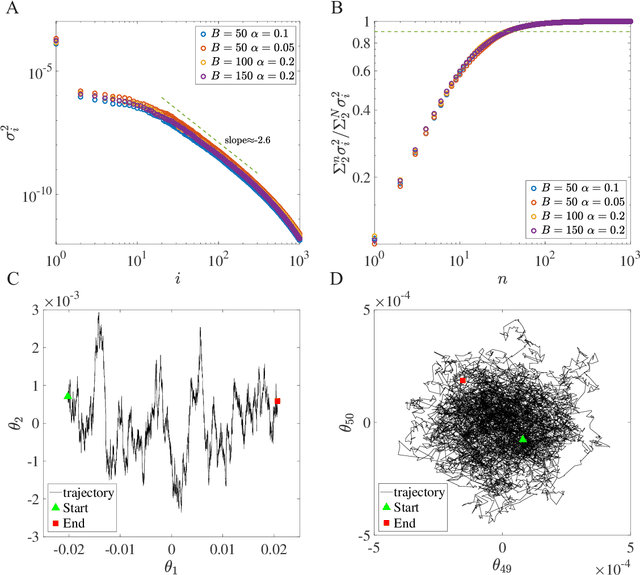
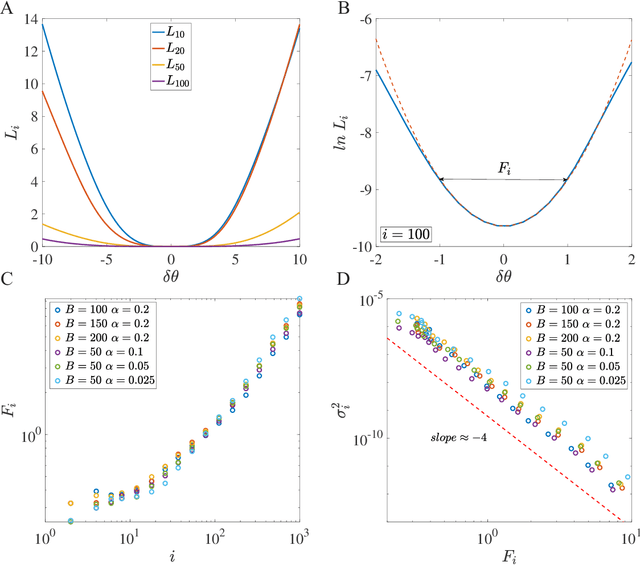
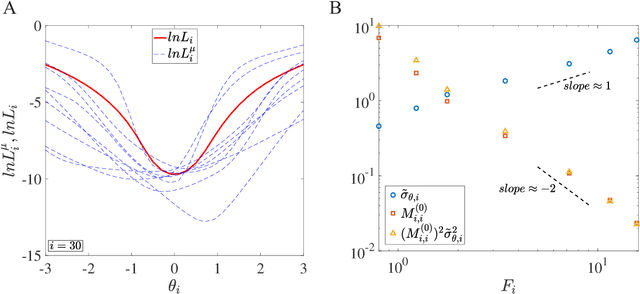
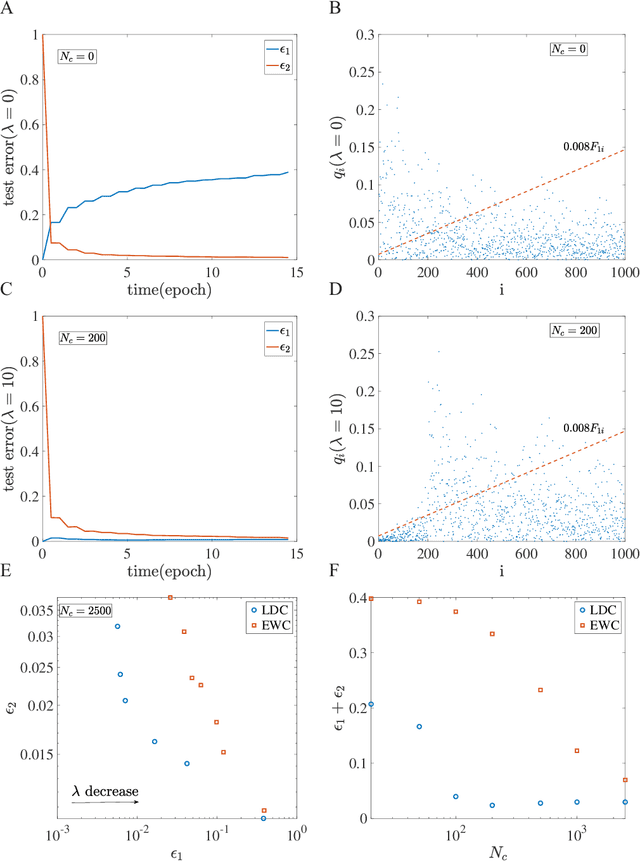
Abstract:Despite the tremendous success of Stochastic Gradient Descent (SGD) algorithm in deep learning, little is known about how SGD finds generalizable solutions in the high-dimensional weight space. By analyzing the learning dynamics and loss function landscape, we discover a robust inverse relation between the weight variance and the landscape flatness (inverse of curvature) for all SGD-based learning algorithms. To explain the inverse variance-flatness relation, we develop a random landscape theory, which shows that the SGD noise strength (effective temperature) depends inversely on the landscape flatness. Our study indicates that SGD attains a self-tuned landscape-dependent annealing strategy to find generalizable solutions at the flat minima of the landscape. Finally, we demonstrate how these new theoretical insights lead to more efficient algorithms, e.g., for avoiding catastrophic forgetting.
Continual Learning with Self-Organizing Maps
Apr 19, 2019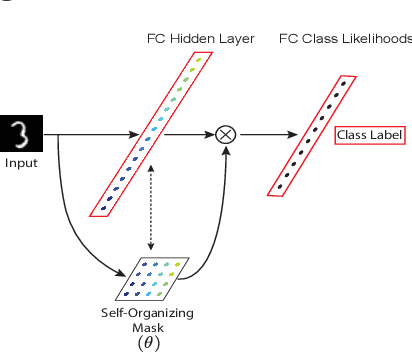
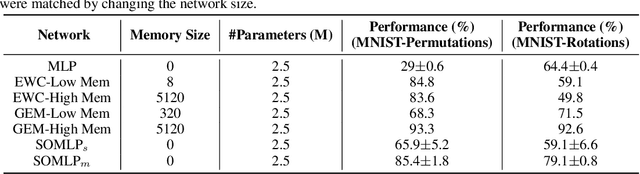
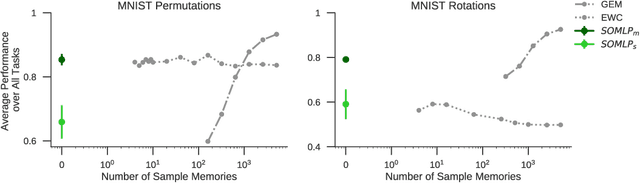

Abstract:Despite remarkable successes achieved by modern neural networks in a wide range of applications, these networks perform best in domain-specific stationary environments where they are trained only once on large-scale controlled data repositories. When exposed to non-stationary learning environments, current neural networks tend to forget what they had previously learned, a phenomena known as catastrophic forgetting. Most previous approaches to this problem rely on memory replay buffers which store samples from previously learned tasks, and use them to regularize the learning on new ones. This approach suffers from the important disadvantage of not scaling well to real-life problems in which the memory requirements become enormous. We propose a memoryless method that combines standard supervised neural networks with self-organizing maps to solve the continual learning problem. The role of the self-organizing map is to adaptively cluster the inputs into appropriate task contexts - without explicit labels - and allocate network resources accordingly. Thus, it selectively routes the inputs in accord with previous experience, ensuring that past learning is maintained and does not interfere with current learning. Out method is intuitive, memoryless, and performs on par with current state-of-the-art approaches on standard benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge