The activity-weight duality in feed forward neural networks: The geometric determinants of generalization
Paper and Code
Mar 22, 2022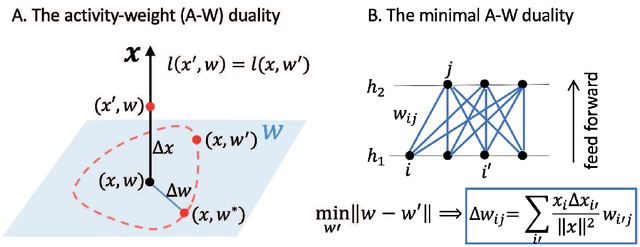

One of the fundamental problems in machine learning is generalization. In neural network models with a large number of weights (parameters), many solutions can be found to fit the training data equally well. The key question is which solution can describe testing data not in the training set. Here, we report the discovery of an exact duality (equivalence) between changes in activities in a given layer of neurons and changes in weights that connect to the next layer of neurons in a densely connected layer in any feed forward neural network. The activity-weight (A-W) duality allows us to map variations in inputs (data) to variations of the corresponding dual weights. By using this mapping, we show that the generalization loss can be decomposed into a sum of contributions from different eigen-directions of the Hessian matrix of the loss function at the solution in weight space. The contribution from a given eigen-direction is the product of two geometric factors (determinants): the sharpness of the loss landscape and the standard deviation of the dual weights, which is found to scale with the weight norm of the solution. Our results provide an unified framework, which we used to reveal how different regularization schemes (weight decay, stochastic gradient descent with different batch sizes and learning rates, dropout), training data size, and labeling noise affect generalization performance by controlling either one or both of these two geometric determinants for generalization. These insights can be used to guide development of algorithms for finding more generalizable solutions in overparametrized neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge