Stochastic gradient descent introduces an effective landscape-dependent regularization favoring flat solutions

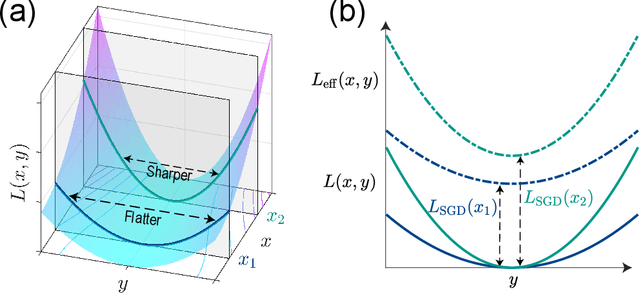
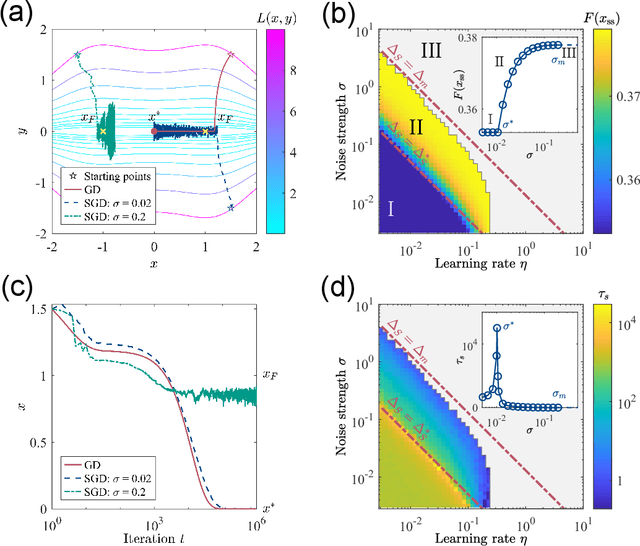
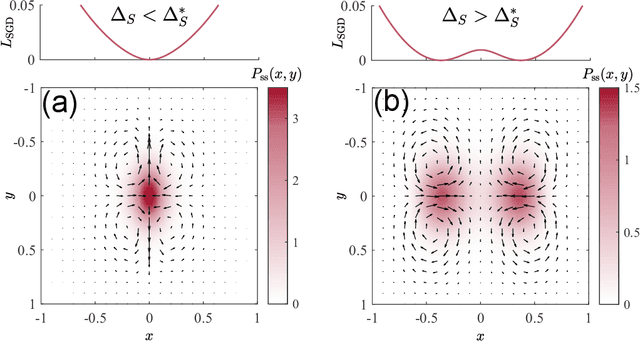
Generalization is one of the most important problems in deep learning (DL). In the overparameterized regime in neural networks, there exist many low-loss solutions that fit the training data equally well. The key question is which solution is more generalizable. Empirical studies showed a strong correlation between flatness of the loss landscape at a solution and its generalizability, and stochastic gradient descent (SGD) is crucial in finding the flat solutions. To understand how SGD drives the learning system to flat solutions, we construct a simple model whose loss landscape has a continuous set of degenerate (or near degenerate) minima. By solving the Fokker-Planck equation of the underlying stochastic learning dynamics, we show that due to its strong anisotropy the SGD noise introduces an additional effective loss term that decreases with flatness and has an overall strength that increases with the learning rate and batch-to-batch variation. We find that the additional landscape-dependent SGD-loss breaks the degeneracy and serves as an effective regularization for finding flat solutions. Furthermore, a stronger SGD noise shortens the convergence time to the flat solutions. However, we identify an upper bound for the SGD noise beyond which the system fails to converge. Our results not only elucidate the role of SGD for generalization they may also have important implications for hyperparameter selection for learning efficiently without divergence.