Non-Euclidean Mixture Model for Social Network Embedding

It is largely agreed that social network links are formed due to either homophily or social influence. Inspired by this, we aim at understanding the generation of links via providing a novel embedding-based graph formation model. Different from existing graph representation learning, where link generation probabilities are defined as a simple function of the corresponding node embeddings, we model the link generation as a mixture model of the two factors. In addition, we model the homophily factor in spherical space and the influence factor in hyperbolic space to accommodate the fact that (1) homophily results in cycles and (2) influence results in hierarchies in networks. We also design a special projection to align these two spaces. We call this model Non-Euclidean Mixture Model, i.e., NMM. We further integrate NMM with our non-Euclidean graph variational autoencoder (VAE) framework, NMM-GNN. NMM-GNN learns embeddings through a unified framework which uses non-Euclidean GNN encoders, non-Euclidean Gaussian priors, a non-Euclidean decoder, and a novel space unification loss component to unify distinct non-Euclidean geometric spaces. Experiments on public datasets show NMM-GNN significantly outperforms state-of-the-art baselines on social network generation and classification tasks, demonstrating its ability to better explain how the social network is formed.

A Survey on Graph Neural Network Acceleration: Algorithms, Systems, and Customized Hardware

Graph neural networks (GNNs) are emerging for machine learning research on graph-structured data. GNNs achieve state-of-the-art performance on many tasks, but they face scalability challenges when it comes to real-world applications that have numerous data and strict latency requirements. Many studies have been conducted on how to accelerate GNNs in an effort to address these challenges. These acceleration techniques touch on various aspects of the GNN pipeline, from smart training and inference algorithms to efficient systems and customized hardware. As the amount of research on GNN acceleration has grown rapidly, there lacks a systematic treatment to provide a unified view and address the complexity of relevant works. In this survey, we provide a taxonomy of GNN acceleration, review the existing approaches, and suggest future research directions. Our taxonomic treatment of GNN acceleration connects the existing works and sets the stage for further development in this area.

Dissimilar Nodes Improve Graph Active Learning

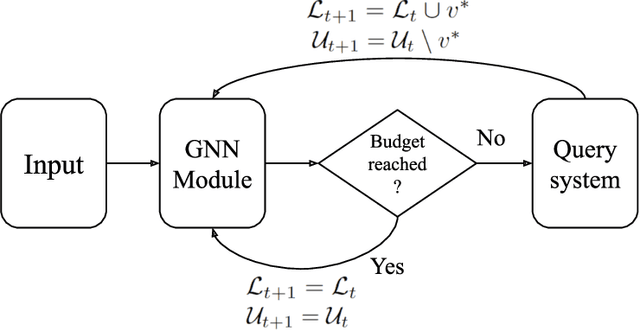
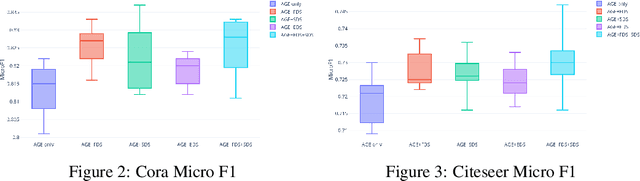
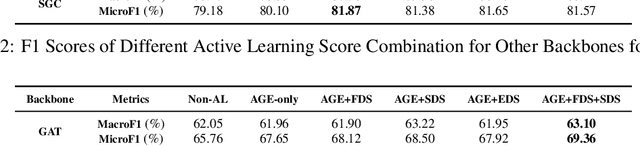
Training labels for graph embedding algorithms could be costly to obtain in many practical scenarios. Active learning (AL) algorithms are very helpful to obtain the most useful labels for training while keeping the total number of label queries under a certain budget. The existing Active Graph Embedding framework proposes to use centrality score, density score, and entropy score to evaluate the value of unlabeled nodes, and it has been shown to be capable of bringing some improvement to the node classification tasks of Graph Convolutional Networks. However, when evaluating the importance of unlabeled nodes, it fails to consider the influence of existing labeled nodes on the value of unlabeled nodes. In other words, given the same unlabeled node, the computed informative score is always the same and is agnostic to the labeled node set. With the aim to address this limitation, in this work, we introduce 3 dissimilarity-based information scores for active learning: feature dissimilarity score (FDS), structure dissimilarity score (SDS), and embedding dissimilarity score (EDS). We find out that those three scores are able to take the influence of the labeled set on the value of unlabeled candidates into consideration, boosting our AL performance. According to experiments, our newly proposed scores boost the classification accuracy by 2.1% on average and are capable of generalizing to different Graph Neural Network architectures.

Layer-Dependent Importance Sampling for Training Deep and Large Graph Convolutional Networks

Graph convolutional networks (GCNs) have recently received wide attentions, due to their successful applications in different graph tasks and different domains. Training GCNs for a large graph, however, is still a challenge. Original full-batch GCN training requires calculating the representation of all the nodes in the graph per GCN layer, which brings in high computation and memory costs. To alleviate this issue, several sampling-based methods have been proposed to train GCNs on a subset of nodes. Among them, the node-wise neighbor-sampling method recursively samples a fixed number of neighbor nodes, and thus its computation cost suffers from exponential growing neighbor size; while the layer-wise importance-sampling method discards the neighbor-dependent constraints, and thus the nodes sampled across layer suffer from sparse connection problem. To deal with the above two problems, we propose a new effective sampling algorithm called LAyer-Dependent ImportancE Sampling (LADIES). Based on the sampled nodes in the upper layer, LADIES selects their neighborhood nodes, constructs a bipartite subgraph and computes the importance probability accordingly. Then, it samples a fixed number of nodes by the calculated probability, and recursively conducts such procedure per layer to construct the whole computation graph. We prove theoretically and experimentally, that our proposed sampling algorithm outperforms the previous sampling methods in terms of both time and memory costs. Furthermore, LADIES is shown to have better generalization accuracy than original full-batch GCN, due to its stochastic nature.