Non-Euclidean Mixture Model for Social Network Embedding

It is largely agreed that social network links are formed due to either homophily or social influence. Inspired by this, we aim at understanding the generation of links via providing a novel embedding-based graph formation model. Different from existing graph representation learning, where link generation probabilities are defined as a simple function of the corresponding node embeddings, we model the link generation as a mixture model of the two factors. In addition, we model the homophily factor in spherical space and the influence factor in hyperbolic space to accommodate the fact that (1) homophily results in cycles and (2) influence results in hierarchies in networks. We also design a special projection to align these two spaces. We call this model Non-Euclidean Mixture Model, i.e., NMM. We further integrate NMM with our non-Euclidean graph variational autoencoder (VAE) framework, NMM-GNN. NMM-GNN learns embeddings through a unified framework which uses non-Euclidean GNN encoders, non-Euclidean Gaussian priors, a non-Euclidean decoder, and a novel space unification loss component to unify distinct non-Euclidean geometric spaces. Experiments on public datasets show NMM-GNN significantly outperforms state-of-the-art baselines on social network generation and classification tasks, demonstrating its ability to better explain how the social network is formed.

Hierarchical Attention Models for Multi-Relational Graphs

We present Bi-Level Attention-Based Relational Graph Convolutional Networks (BR-GCN), unique neural network architectures that utilize masked self-attentional layers with relational graph convolutions, to effectively operate on highly multi-relational data. BR-GCN models use bi-level attention to learn node embeddings through (1) node-level attention, and (2) relation-level attention. The node-level self-attentional layers use intra-relational graph interactions to learn relation-specific node embeddings using a weighted aggregation of neighborhood features in a sparse subgraph region. The relation-level self-attentional layers use inter-relational graph interactions to learn the final node embeddings using a weighted aggregation of relation-specific node embeddings. The BR-GCN bi-level attention mechanism extends Transformer-based multiplicative attention from the natural language processing (NLP) domain, and Graph Attention Networks (GAT)-based attention, to large-scale heterogeneous graphs (HGs). On node classification, BR-GCN outperforms baselines from 0.29% to 14.95% as a stand-alone model, and on link prediction, BR-GCN outperforms baselines from 0.02% to 7.40% as an auto-encoder model. We also conduct ablation studies to evaluate the quality of BR-GCN's relation-level attention and discuss how its learning of graph structure may be transferred to enrich other graph neural networks (GNNs). Through various experiments, we show that BR-GCN's attention mechanism is both scalable and more effective in learning compared to state-of-the-art GNNs.

Bi-Level Attention Graph Neural Networks

Recent graph neural networks (GNNs) with the attention mechanism have historically been limited to small-scale homogeneous graphs (HoGs). However, GNNs handling heterogeneous graphs (HeGs), which contain several entity and relation types, all have shortcomings in handling attention. Most GNNs that learn graph attention for HeGs learn either node-level or relation-level attention, but not both, limiting their ability to predict both important entities and relations in the HeG. Even the best existing method that learns both levels of attention has the limitation of assuming graph relations are independent and that its learned attention disregards this dependency association. To effectively model both multi-relational and multi-entity large-scale HeGs, we present Bi-Level Attention Graph Neural Networks (BA-GNN), scalable neural networks (NNs) that use a novel bi-level graph attention mechanism. BA-GNN models both node-node and relation-relation interactions in a personalized way, by hierarchically attending to both types of information from local neighborhood contexts instead of the global graph context. Rigorous experiments on seven real-world HeGs show BA-GNN consistently outperforms all baselines, and demonstrate quality and transferability of its learned relation-level attention to improve performance of other GNNs.

Dual-Geometric Space Embedding Model for Two-View Knowledge Graphs

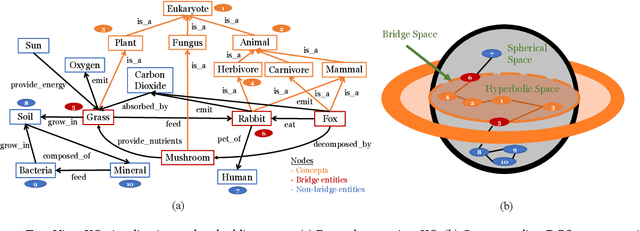
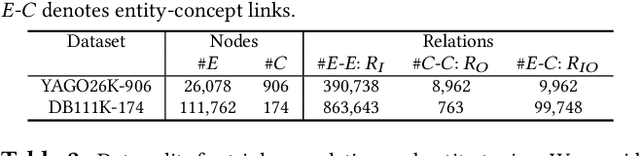
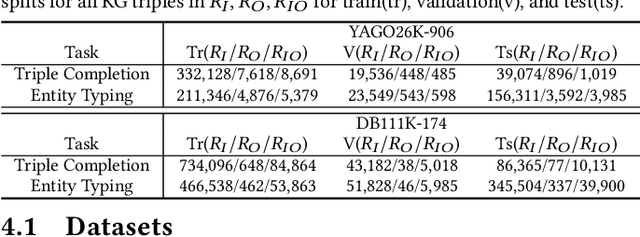
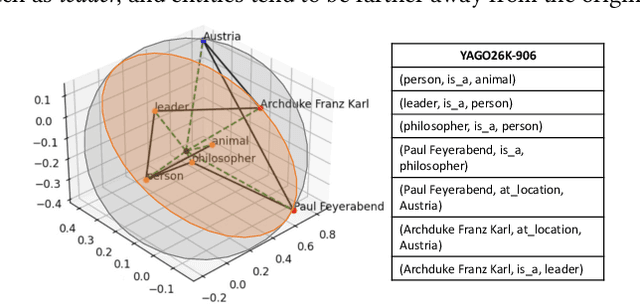
Two-view knowledge graphs (KGs) jointly represent two components: an ontology view for abstract and commonsense concepts, and an instance view for specific entities that are instantiated from ontological concepts. As such, these KGs contain heterogeneous structures that are hierarchical, from the ontology-view, and cyclical, from the instance-view. Despite these various structures in KGs, most recent works on embedding KGs assume that the entire KG belongs to only one of the two views but not both simultaneously. For works that seek to put both views of the KG together, the instance and ontology views are assumed to belong to the same geometric space, such as all nodes embedded in the same Euclidean space or non-Euclidean product space, an assumption no longer reasonable for two-view KGs where different portions of the graph exhibit different structures. To address this issue, we define and construct a dual-geometric space embedding model (DGS) that models two-view KGs using a complex non-Euclidean geometric space, by embedding different portions of the KG in different geometric spaces. DGS utilizes the spherical space, hyperbolic space, and their intersecting space in a unified framework for learning embeddings. Furthermore, for the spherical space, we propose novel closed spherical space operators that directly operate in the spherical space without the need for mapping to an approximate tangent space. Experiments on public datasets show that DGS significantly outperforms previous state-of-the-art baseline models on KG completion tasks, demonstrating its ability to better model heterogeneous structures in KGs.

Question-Answer Sentence Graph for Joint Modeling Answer Selection

This research studies graph-based approaches for Answer Sentence Selection (AS2), an essential component for building retrieval-based Question Answering systems. Given a question, our model creates a small-scale relevant training graph to perform more accurate AS2. The nodes of the graphs are question-answer pairs, where the answers are also sentences. We train and apply state-of-the-art models for computing scores between question-question, question-answer, and answer-answer pairs. We apply thresholding to the relevance scores for creating edges between nodes. Finally, we apply Graph Neural Networks to the obtained graph to perform joint learning and inference for solving the AS2 task. The experiments on two well-known academic benchmarks and a real-world dataset show that our approach consistently outperforms state-of-the-art models.

Software Language Comprehension using a Program-Derived Semantic Graph

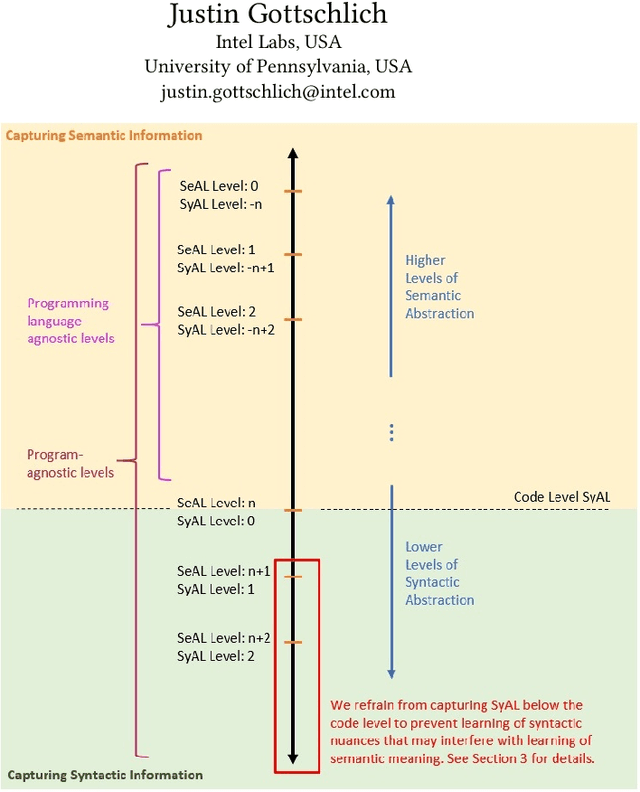
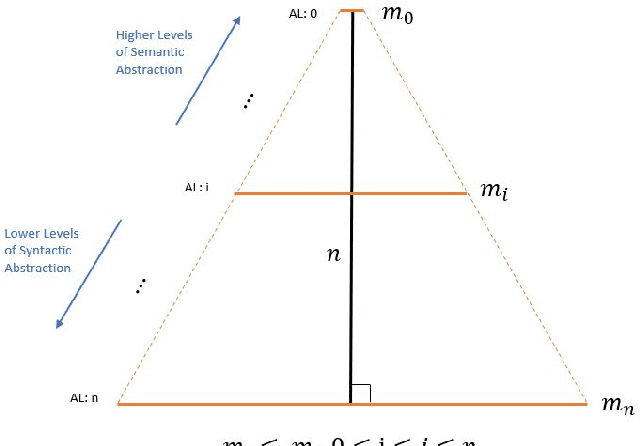
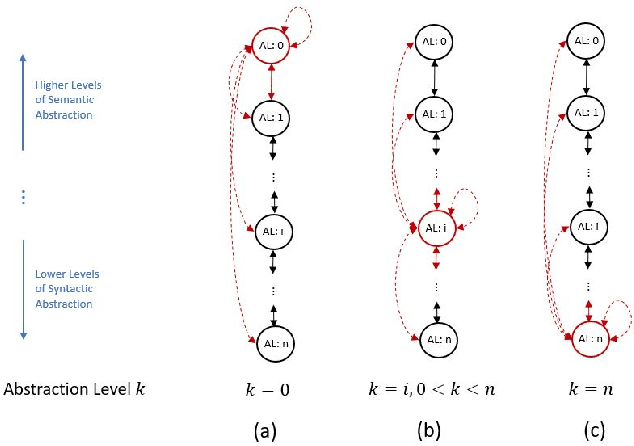
Traditional code transformation structures, such as an abstract syntax tree, may have limitations in their ability to extract semantic meaning from code. Others have begun to work on this issue, such as the state-of-the-art Aroma system and its simplified parse tree (SPT). Continuing this research direction, we present a new graphical structure to capture semantics from code using what we refer to as a program-derived semantic graph (PSG). The principle behind the PSG is to provide a single structure that can capture program semantics at many levels of granularity. Thus, the PSG is hierarchical in nature. Moreover, because the PSG may have cycles due to dependencies in semantic layers, it is a graph, not a tree. In this paper, we describe the PSG and its fundamental structural differences to the Aroma's SPT. Although our work in the PSG is in its infancy, our early results indicate it is a promising new research direction to explore to automatically extract program semantics.