Dual-Geometric Space Embedding Model for Two-View Knowledge Graphs
Paper and Code
Sep 19, 2022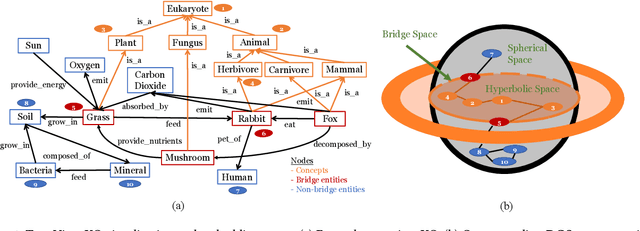
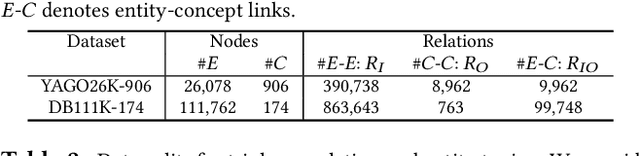
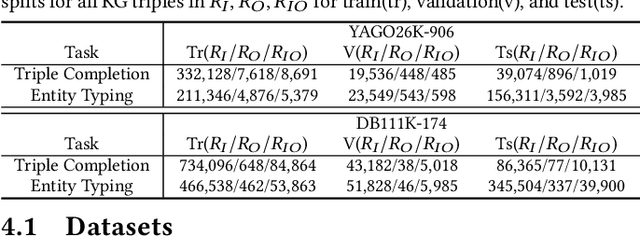
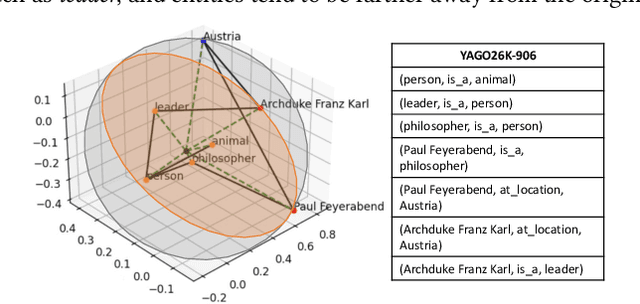
Two-view knowledge graphs (KGs) jointly represent two components: an ontology view for abstract and commonsense concepts, and an instance view for specific entities that are instantiated from ontological concepts. As such, these KGs contain heterogeneous structures that are hierarchical, from the ontology-view, and cyclical, from the instance-view. Despite these various structures in KGs, most recent works on embedding KGs assume that the entire KG belongs to only one of the two views but not both simultaneously. For works that seek to put both views of the KG together, the instance and ontology views are assumed to belong to the same geometric space, such as all nodes embedded in the same Euclidean space or non-Euclidean product space, an assumption no longer reasonable for two-view KGs where different portions of the graph exhibit different structures. To address this issue, we define and construct a dual-geometric space embedding model (DGS) that models two-view KGs using a complex non-Euclidean geometric space, by embedding different portions of the KG in different geometric spaces. DGS utilizes the spherical space, hyperbolic space, and their intersecting space in a unified framework for learning embeddings. Furthermore, for the spherical space, we propose novel closed spherical space operators that directly operate in the spherical space without the need for mapping to an approximate tangent space. Experiments on public datasets show that DGS significantly outperforms previous state-of-the-art baseline models on KG completion tasks, demonstrating its ability to better model heterogeneous structures in KGs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge