SFR-GNN: Simple and Fast Robust GNNs against Structural Attacks

Graph Neural Networks (GNNs) have demonstrated commendable performance for graph-structured data. Yet, GNNs are often vulnerable to adversarial structural attacks as embedding generation relies on graph topology. Existing efforts are dedicated to purifying the maliciously modified structure or applying adaptive aggregation, thereby enhancing the robustness against adversarial structural attacks. It is inevitable for a defender to consume heavy computational costs due to lacking prior knowledge about modified structures. To this end, we propose an efficient defense method, called Simple and Fast Robust Graph Neural Network (SFR-GNN), supported by mutual information theory. The SFR-GNN first pre-trains a GNN model using node attributes and then fine-tunes it over the modified graph in the manner of contrastive learning, which is free of purifying modified structures and adaptive aggregation, thus achieving great efficiency gains. Consequently, SFR-GNN exhibits a 24%--162% speedup compared to advanced robust models, demonstrating superior robustness for node classification tasks.

Adversarially Robust Signed Graph Contrastive Learning from Balance Augmentation

Signed graphs consist of edges and signs, which can be separated into structural information and balance-related information, respectively. Existing signed graph neural networks (SGNNs) typically rely on balance-related information to generate embeddings. Nevertheless, the emergence of recent adversarial attacks has had a detrimental impact on the balance-related information. Similar to how structure learning can restore unsigned graphs, balance learning can be applied to signed graphs by improving the balance degree of the poisoned graph. However, this approach encounters the challenge "Irreversibility of Balance-related Information" - while the balance degree improves, the restored edges may not be the ones originally affected by attacks, resulting in poor defense effectiveness. To address this challenge, we propose a robust SGNN framework called Balance Augmented-Signed Graph Contrastive Learning (BA-SGCL), which combines Graph Contrastive Learning principles with balance augmentation techniques. Experimental results demonstrate that BA-SGCL not only enhances robustness against existing adversarial attacks but also achieves superior performance on link sign prediction task across various datasets.

Universally Robust Graph Neural Networks by Preserving Neighbor Similarity

Despite the tremendous success of graph neural networks in learning relational data, it has been widely investigated that graph neural networks are vulnerable to structural attacks on homophilic graphs. Motivated by this, a surge of robust models is crafted to enhance the adversarial robustness of graph neural networks on homophilic graphs. However, the vulnerability based on heterophilic graphs remains a mystery to us. To bridge this gap, in this paper, we start to explore the vulnerability of graph neural networks on heterophilic graphs and theoretically prove that the update of the negative classification loss is negatively correlated with the pairwise similarities based on the powered aggregated neighbor features. This theoretical proof explains the empirical observations that the graph attacker tends to connect dissimilar node pairs based on the similarities of neighbor features instead of ego features both on homophilic and heterophilic graphs. In this way, we novelly introduce a novel robust model termed NSPGNN which incorporates a dual-kNN graphs pipeline to supervise the neighbor similarity-guided propagation. This propagation utilizes the low-pass filter to smooth the features of node pairs along the positive kNN graphs and the high-pass filter to discriminate the features of node pairs along the negative kNN graphs. Extensive experiments on both homophilic and heterophilic graphs validate the universal robustness of NSPGNN compared to the state-of-the-art methods.

Graph Anomaly Detection at Group Level: A Topology Pattern Enhanced Unsupervised Approach

Graph anomaly detection (GAD) has achieved success and has been widely applied in various domains, such as fraud detection, cybersecurity, finance security, and biochemistry. However, existing graph anomaly detection algorithms focus on distinguishing individual entities (nodes or graphs) and overlook the possibility of anomalous groups within the graph. To address this limitation, this paper introduces a novel unsupervised framework for a new task called Group-level Graph Anomaly Detection (Gr-GAD). The proposed framework first employs a variant of Graph AutoEncoder (GAE) to locate anchor nodes that belong to potential anomaly groups by capturing long-range inconsistencies. Subsequently, group sampling is employed to sample candidate groups, which are then fed into the proposed Topology Pattern-based Graph Contrastive Learning (TPGCL) method. TPGCL utilizes the topology patterns of groups as clues to generate embeddings for each candidate group and thus distinct anomaly groups. The experimental results on both real-world and synthetic datasets demonstrate that the proposed framework shows superior performance in identifying and localizing anomaly groups, highlighting it as a promising solution for Gr-GAD. Datasets and codes of the proposed framework are at the github repository https://anonymous.4open.science/r/Topology-Pattern-Enhanced-Unsupervised-Group-level-Graph-Anomaly-Detection.

Homophily-Driven Sanitation View for Robust Graph Contrastive Learning

We investigate adversarial robustness of unsupervised Graph Contrastive Learning (GCL) against structural attacks. First, we provide a comprehensive empirical and theoretical analysis of existing attacks, revealing how and why they downgrade the performance of GCL. Inspired by our analytic results, we present a robust GCL framework that integrates a homophily-driven sanitation view, which can be learned jointly with contrastive learning. A key challenge this poses, however, is the non-differentiable nature of the sanitation objective. To address this challenge, we propose a series of techniques to enable gradient-based end-to-end robust GCL. Moreover, we develop a fully unsupervised hyperparameter tuning method which, unlike prior approaches, does not require knowledge of node labels. We conduct extensive experiments to evaluate the performance of our proposed model, GCHS (Graph Contrastive Learning with Homophily-driven Sanitation View), against two state of the art structural attacks on GCL. Our results demonstrate that GCHS consistently outperforms all state of the art baselines in terms of the quality of generated node embeddings as well as performance on two important downstream tasks.

Labeled Subgraph Entropy Kernel

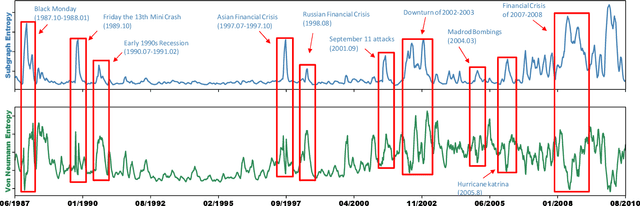
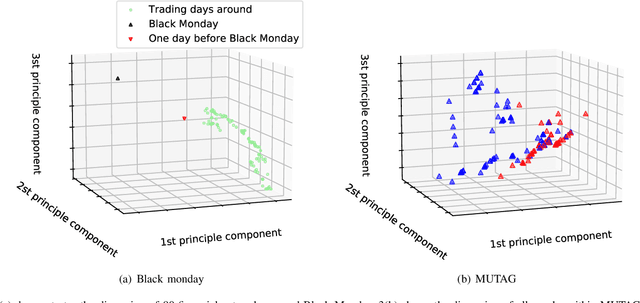
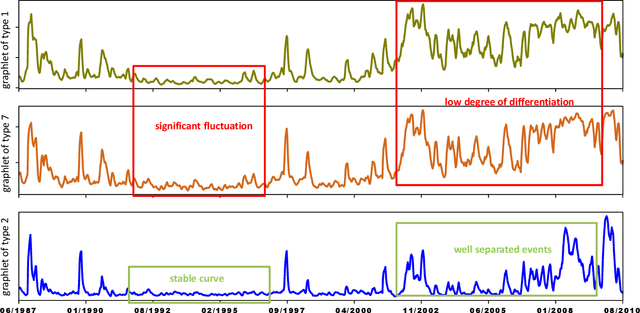
In recent years, kernel methods are widespread in tasks of similarity measuring. Specifically, graph kernels are widely used in fields of bioinformatics, chemistry and financial data analysis. However, existing methods, especially entropy based graph kernels are subject to large computational complexity and the negligence of node-level information. In this paper, we propose a novel labeled subgraph entropy graph kernel, which performs well in structural similarity assessment. We design a dynamic programming subgraph enumeration algorithm, which effectively reduces the time complexity. Specially, we propose labeled subgraph, which enriches substructure topology with semantic information. Analogizing the cluster expansion process of gas cluster in statistical mechanics, we re-derive the partition function and calculate the global graph entropy to characterize the network. In order to test our method, we apply several real-world datasets and assess the effects in different tasks. To capture more experiment details, we quantitatively and qualitatively analyze the contribution of different topology structures. Experimental results successfully demonstrate the effectiveness of our method which outperforms several state-of-the-art methods.

Simple yet Effective Gradient-Free Graph Convolutional Networks

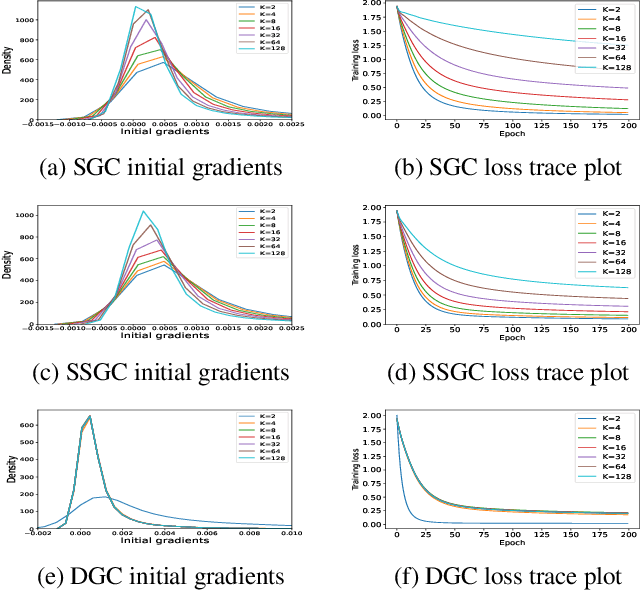
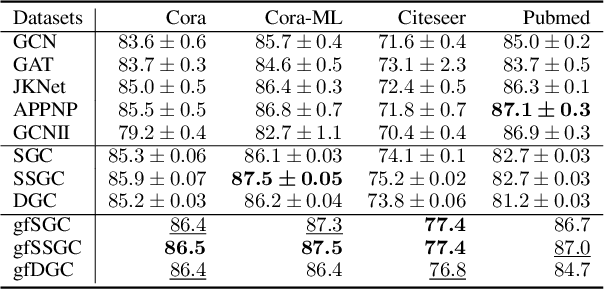
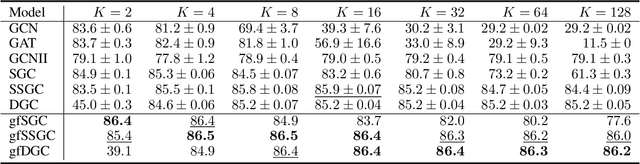
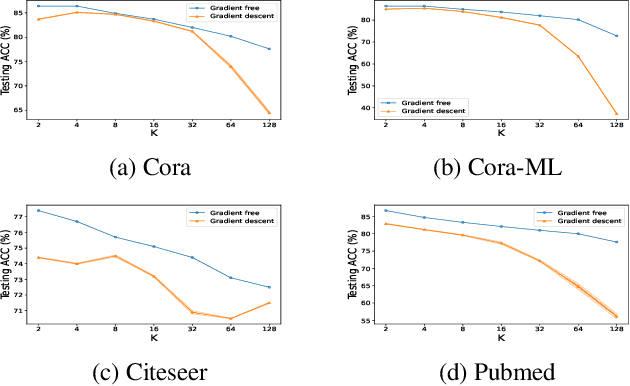
Linearized Graph Neural Networks (GNNs) have attracted great attention in recent years for graph representation learning. Compared with nonlinear Graph Neural Network (GNN) models, linearized GNNs are much more time-efficient and can achieve comparable performances on typical downstream tasks such as node classification. Although some linearized GNN variants are purposely crafted to mitigate ``over-smoothing", empirical studies demonstrate that they still somehow suffer from this issue. In this paper, we instead relate over-smoothing with the vanishing gradient phenomenon and craft a gradient-free training framework to achieve more efficient and effective linearized GNNs which can significantly overcome over-smoothing and enhance the generalization of the model. The experimental results demonstrate that our methods achieve better and more stable performances on node classification tasks with varying depths and cost much less training time.

Decompositional Quantum Graph Neural Network

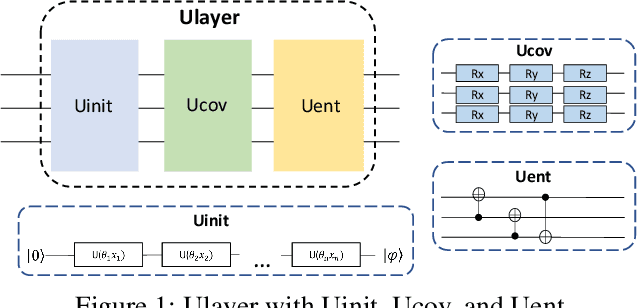
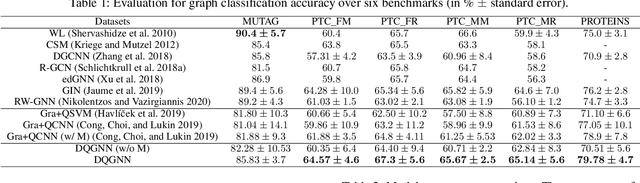
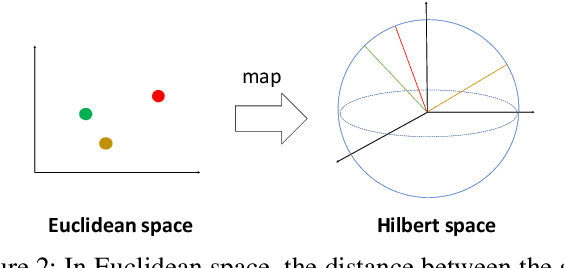
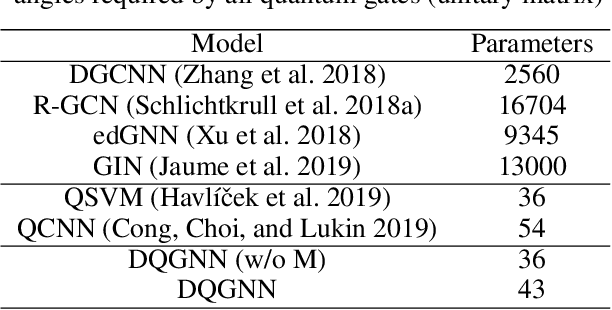
Quantum machine learning is a fast emerging field that aims to tackle machine learning using quantum algorithms and quantum computing. Due to the lack of physical qubits and an effective means to map real-world data from Euclidean space to Hilbert space, most of these methods focus on quantum analogies or process simulations rather than devising concrete architectures based on qubits. In this paper, we propose a novel hybrid quantum-classical algorithm for graph-structured data, which we refer to as the Decompositional Quantum Graph Neural Network (DQGNN). DQGNN implements the GNN theoretical framework using the tensor product and unity matrices representation, which greatly reduces the number of model parameters required. When controlled by a classical computer, DQGNN can accommodate arbitrarily sized graphs by processing substructures from the input graph using a modestly-sized quantum device. The architecture is based on a novel mapping from real-world data to Hilbert space. This mapping maintains the distance relations present in the data and reduces information loss. Experimental results show that the proposed method outperforms competitive state-of-the-art models with only 1.68\% parameters compared to those models.

Two-level Graph Neural Network

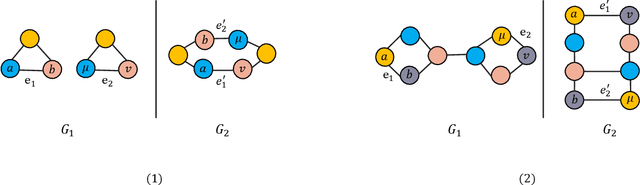
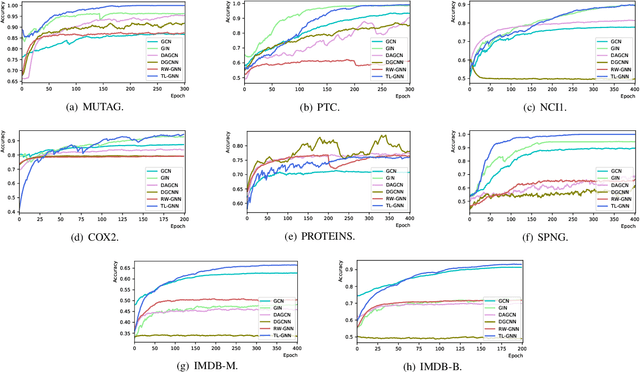
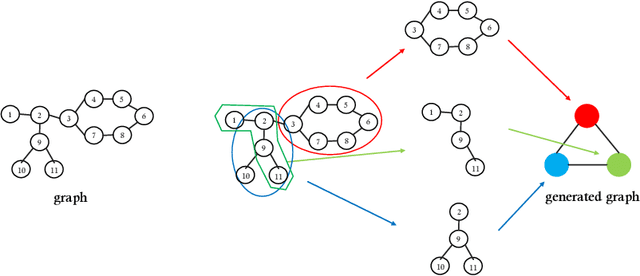
Graph Neural Networks (GNNs) are recently proposed neural network structures for the processing of graph-structured data. Due to their employed neighbor aggregation strategy, existing GNNs focus on capturing node-level information and neglect high-level information. Existing GNNs therefore suffer from representational limitations caused by the Local Permutation Invariance (LPI) problem. To overcome these limitations and enrich the features captured by GNNs, we propose a novel GNN framework, referred to as the Two-level GNN (TL-GNN). This merges subgraph-level information with node-level information. Moreover, we provide a mathematical analysis of the LPI problem which demonstrates that subgraph-level information is beneficial to overcoming the problems associated with LPI. A subgraph counting method based on the dynamic programming algorithm is also proposed, and this has time complexity is O(n^3), n is the number of nodes of a graph. Experiments show that TL-GNN outperforms existing GNNs and achieves state-of-the-art performance.