Two-level Graph Neural Network
Paper and Code
Jan 03, 2022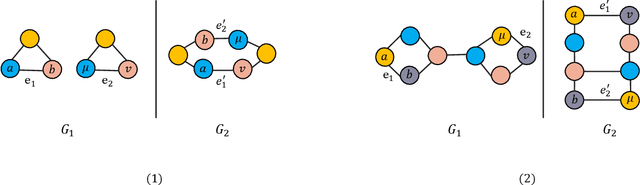
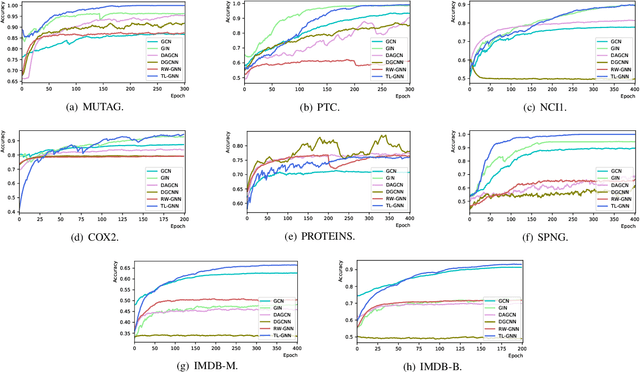
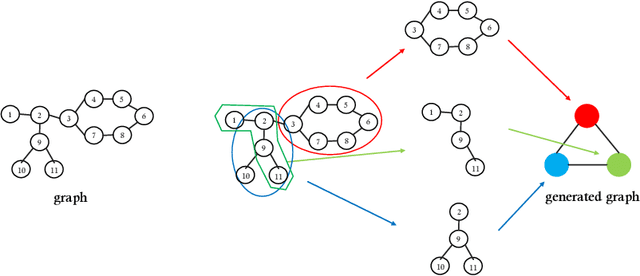
Graph Neural Networks (GNNs) are recently proposed neural network structures for the processing of graph-structured data. Due to their employed neighbor aggregation strategy, existing GNNs focus on capturing node-level information and neglect high-level information. Existing GNNs therefore suffer from representational limitations caused by the Local Permutation Invariance (LPI) problem. To overcome these limitations and enrich the features captured by GNNs, we propose a novel GNN framework, referred to as the Two-level GNN (TL-GNN). This merges subgraph-level information with node-level information. Moreover, we provide a mathematical analysis of the LPI problem which demonstrates that subgraph-level information is beneficial to overcoming the problems associated with LPI. A subgraph counting method based on the dynamic programming algorithm is also proposed, and this has time complexity is O(n^3), n is the number of nodes of a graph. Experiments show that TL-GNN outperforms existing GNNs and achieves state-of-the-art performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge