Labeled Subgraph Entropy Kernel

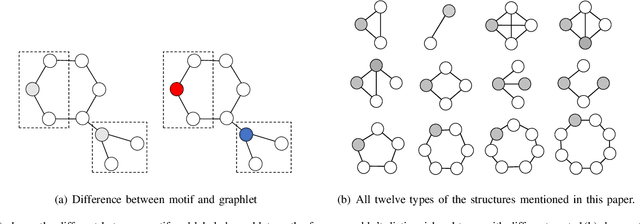
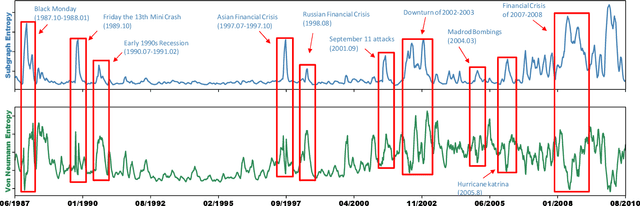
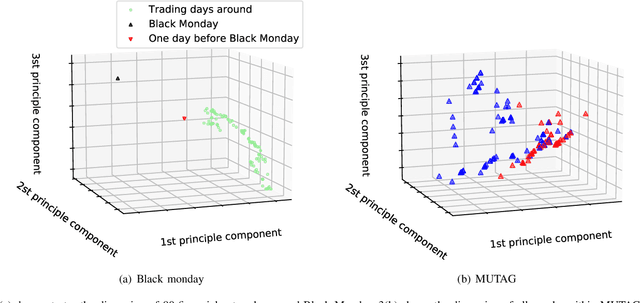
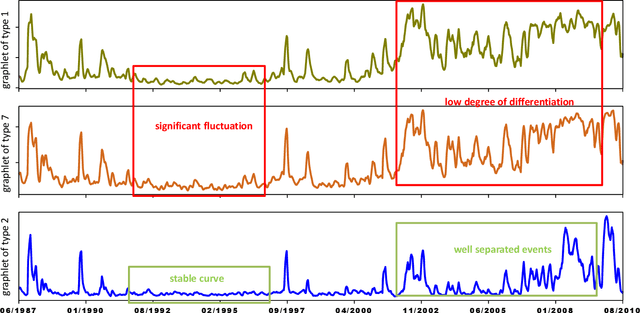
In recent years, kernel methods are widespread in tasks of similarity measuring. Specifically, graph kernels are widely used in fields of bioinformatics, chemistry and financial data analysis. However, existing methods, especially entropy based graph kernels are subject to large computational complexity and the negligence of node-level information. In this paper, we propose a novel labeled subgraph entropy graph kernel, which performs well in structural similarity assessment. We design a dynamic programming subgraph enumeration algorithm, which effectively reduces the time complexity. Specially, we propose labeled subgraph, which enriches substructure topology with semantic information. Analogizing the cluster expansion process of gas cluster in statistical mechanics, we re-derive the partition function and calculate the global graph entropy to characterize the network. In order to test our method, we apply several real-world datasets and assess the effects in different tasks. To capture more experiment details, we quantitatively and qualitatively analyze the contribution of different topology structures. Experimental results successfully demonstrate the effectiveness of our method which outperforms several state-of-the-art methods.

Collaborative Knowledge Graph Fusion by Exploiting the Open Corpus

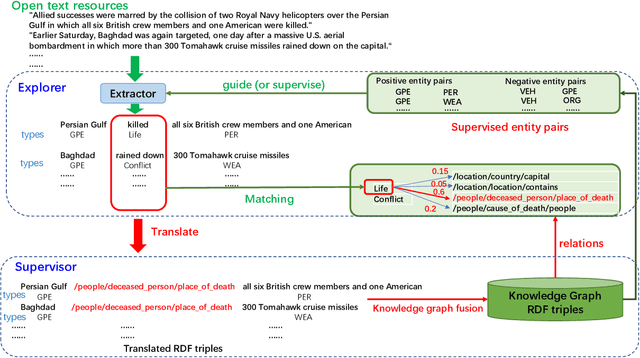
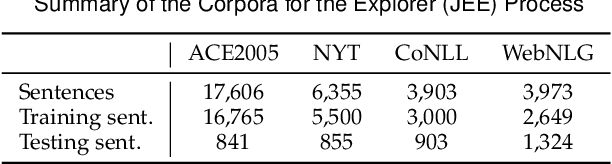
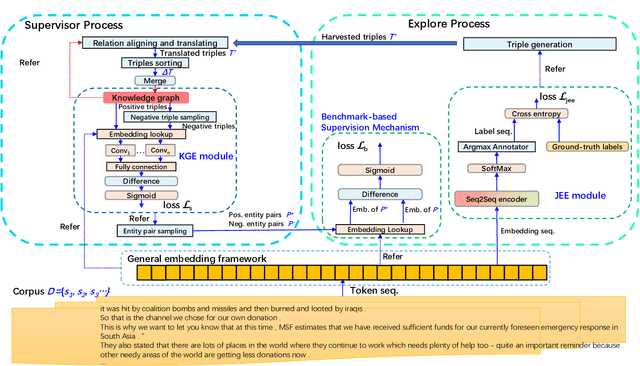
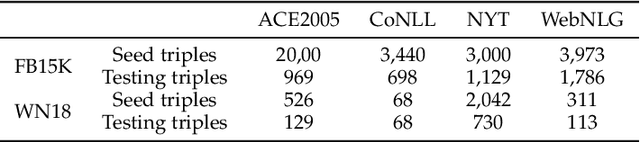
To alleviate the challenges of building Knowledge Graphs (KG) from scratch, a more general task is to enrich a KG using triples from an open corpus, where the obtained triples contain noisy entities and relations. It is challenging to enrich a KG with newly harvested triples while maintaining the quality of the knowledge representation. This paper proposes a system to refine a KG using information harvested from an additional corpus. To this end, we formulate our task as two coupled sub-tasks, namely join event extraction (JEE) and knowledge graph fusion (KGF). We then propose a Collaborative Knowledge Graph Fusion Framework to allow our sub-tasks to mutually assist one another in an alternating manner. More concretely, the explorer carries out the JEE supervised by both the ground-truth annotation and an existing KG provided by the supervisor. The supervisor then evaluates the triples extracted by the explorer and enriches the KG with those that are highly ranked. To implement this evaluation, we further propose a Translated Relation Alignment Scoring Mechanism to align and translate the extracted triples to the prior KG. Experiments verify that this collaboration can both improve the performance of the JEE and the KGF.

Two-level Graph Neural Network

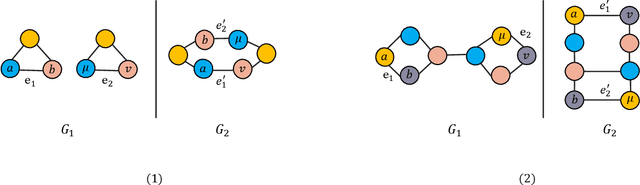
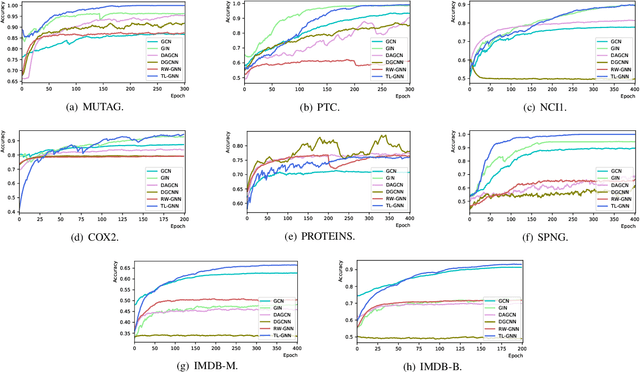
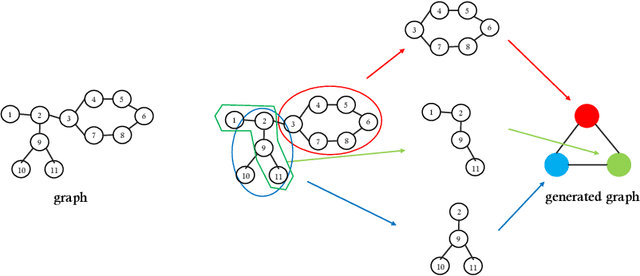
Graph Neural Networks (GNNs) are recently proposed neural network structures for the processing of graph-structured data. Due to their employed neighbor aggregation strategy, existing GNNs focus on capturing node-level information and neglect high-level information. Existing GNNs therefore suffer from representational limitations caused by the Local Permutation Invariance (LPI) problem. To overcome these limitations and enrich the features captured by GNNs, we propose a novel GNN framework, referred to as the Two-level GNN (TL-GNN). This merges subgraph-level information with node-level information. Moreover, we provide a mathematical analysis of the LPI problem which demonstrates that subgraph-level information is beneficial to overcoming the problems associated with LPI. A subgraph counting method based on the dynamic programming algorithm is also proposed, and this has time complexity is O(n^3), n is the number of nodes of a graph. Experiments show that TL-GNN outperforms existing GNNs and achieves state-of-the-art performance.